Um I thought it was, but I didn't look properly and you did not expressly ask me to look. Sorry. 
I will give you a more comprehensive answer.
First, draw a rough sketch, this will be enough to tell you that y must be greater than 2. It will also tell you that there is only one y value (but 2 x vales for the solution.)
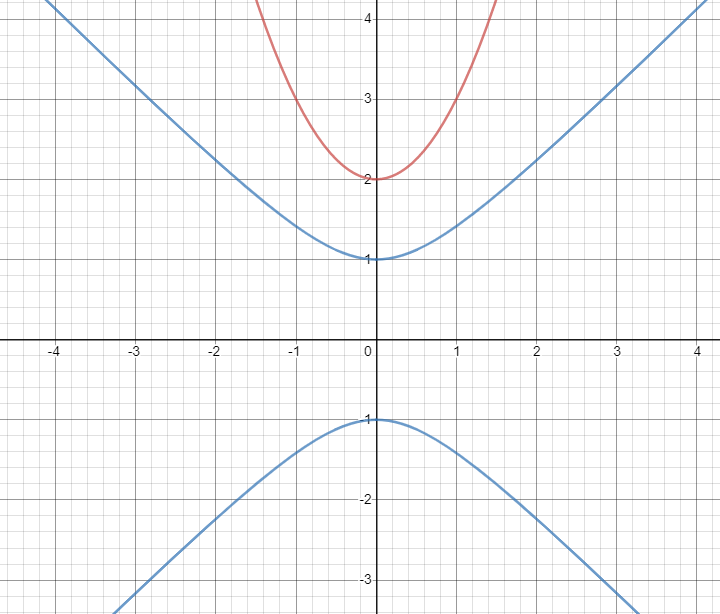
\(y = x^2+2\) is a concave up parabola. The axis of symmetry is the y axis and the vertex is (0,2)
You should have enough knowledge to know this.
--------------------
\( y^2 - mx^2 = 1\) is a hyperbola so long as m is positive real number
Hypperbolas of the form \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) have a vertical axis, the y axis is the axis of symmetry and a ist the y intercept
So in our case, a=+/-1 So the vertices are (0,1) and (0,-1)
So this is our initial sketch. The red is the parabola and the blue is the hyperbola.
m will change the steepness of the hyperbola so you want to find the m that will make the graph look like this.
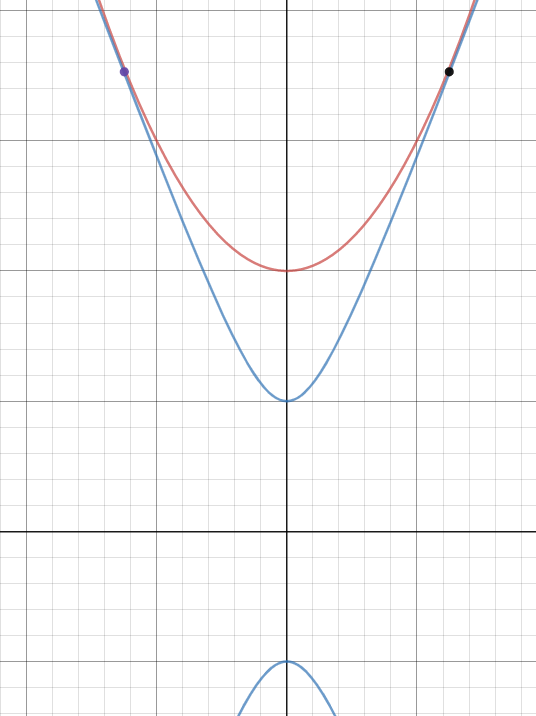
So by now you should at least understand what you are being asked, as far as the outcome goes.
-------------------------------
So now you have to solve
\(y=x^2+2\qquad and \qquad y^2-mx^2=1\qquad \text{simultaneously}\\ \text{we know already}\\ \text{ m is positive and y is positive and there is only one value of y}\)
\(y=x^2+2\qquad and \qquad y^2-mx^2=1\\ x^2=y-2\qquad and \qquad x^2=\frac{1-y^2}{-m}\\ so\\ y-2=\frac{1-y^2}{-m}\\ -my+2m=1-y^2\\ y^2-my+(2m-1)=0\\\)
now solve using the quadratic formula
y will be in terms of m but if you know roughly what it looks like you will know that there is only one solution.
So the discriminant must be 0.
From this, the value of m can be determined.
You are welcome to ask questions (tell me what you have done though)
LaTex:
y=x^2+2\qquad and \qquad y^2-mx^2=1\\
x^2=y-2\qquad and \qquad x^2=\frac{1-y^2}{-m}\\
so\\
y-2=\frac{1-y^2}{-m}\\
-my+2m=1-y^2\\
y^2-my+(2m-1)=0\\