All Answers 358083 Answers

According to the rational root theorem, the possible rational roots are the possibilities of the factors of the constant term divided by factors of the coefficient of the highest degree term.

Therefore, the possible roots are \(\pm1,\pm2,\pm3,\pm6\).

You could test out these individual values and plug them into the equation.

The ones that work are -3, -1, and 2.

Therefore the factored form of this polynomial is (x+3)(x+1)(x-2)

log₃ (x+2) = - 2

log(x+2) / log 3 = - 2

log(x+2) = - 2 log3

log (x+2) = log3^-2

x+2 = 1/3²

x = -2 + 1/9 = - 17/9

This can be simplified to:

\(3^{-2}=x+2\)

Then, just solve the linear equation:

\(\frac{1}{9}=x+2\\ x=\boxed{-\frac{17}{9}}\)

I am glad you have been persistent.

Keep it up.    

Your answer is closer than mine.

I don't have my earlier working any more.  It beats me where I got those numbers from.  Sorry.

Let me start over.

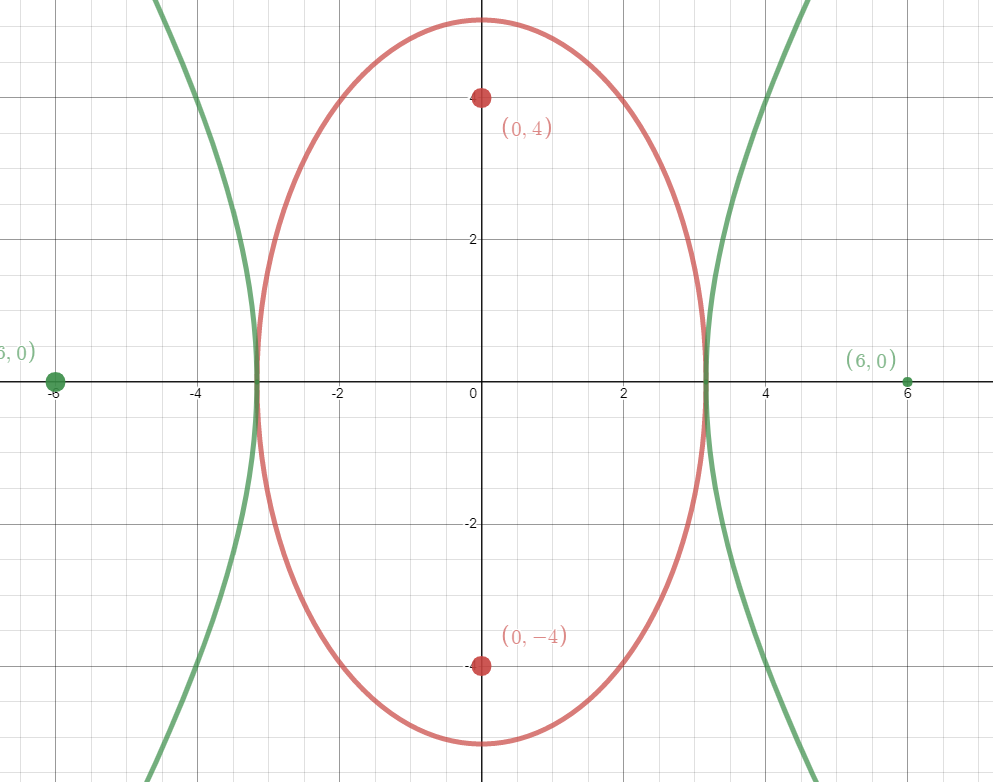
The equation of an ellipse is    \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)

focal length c = 4

If the major axis is horizonal then a > b

If the major axis is vertical then a < b

Since this one has a major axis of  y=0 it is vertical so  a is smaller than b

The focal length is c where

\(c^2=|a^2-b^2|\)

since a < b,

\(c^2=b^2-a^2\\ 16=b^2-a^2\\ \)

For the hyperbola

\(c^2=a^2+b^2\\ 36=a^2+b^2\\\)

solve them simultaneously and you get   \(b=\sqrt{26}\qquad a=\sqrt{10}\)

Here is the graph

120 divided by 3/2 equal 80 because if you add 1.5 + 1.5 equal 2.10

ln( (x-3)⁹ / x¹¹)

find the domain of the rational function
g(x)= 4x / (x+5)(x-6)

Hello Guest!

\(g(x)= \frac{4x}{ (x+5)(x-6)} \)

\((x+5)(x-6)=0 \)

\(x\in\{-5,6\} \)

\(\mathbb D_{g(x)}=\mathbb R |x\in\{-5,6\}\)

  !

Axis of symmetry is x = -b/2a

   vertex will be this value of 'x' and the 'y' value generated when substituting this value into the equation

      zeroes will be :

         factor (x-3)(x-3) = 0     only one zero   x = 3  (same as the axis of symmetry for this parabola)

OK...glad to help....

Thank you. Got it.

8^x                                  9^(x + y)

________  = 64             ________ =   243           

2^(x + y)                          3^(4y)

Write the first as                                  Write  the second as

(2^3)^x                                                     (3^2)^(x + y)                                                                

________  =   64                                   ____________  =    243                           

2^x * 2^y                                                     3^(4y)

2^(3x)                                                        3^(2x) * 3^(2y)

________  =  64                                      _____________   = 243

 2^x * 2^y                                                  3^(2y) * 3^( 2y)                                                   

2^(2x)                                                        3^(2x)

_____  =  64                                           ________  =   243

2^y                                                            3^(2y)

2^(2x - y)  = 2^6                                      3^(2x - 2y)  =  3^5

So

2x - y  = 6   ⇒   -2x + y = -6   (1)

2x - 2y = 5   (2)

add   (1)  and (2)

-y  =  -1

y = 1

2x - 1  = 6

2x  =  7

x =  7/2

2xy  =     2(7/2)(1)   =    7

4/9 of the large hose will take  9/4 of the time    9/4 * 4 hrs = 9 hours/pool   = 1/9  pool /hrs

8 small hoses will take 6/8 of the time                  6/8 * 8 hrs = 6 hrs/pool = 1/6 pool /hrs

1 pool/ (1/9 + 1/6) = 3.6 hrs

Consider if we added the  line  y =  -1

Note that te graph  would cut this line in two places......so...

Two values of  c

T =   ( x^2  + (74 - x)^2 )^(1/2) / 2  +  ( x^2 + 63^2) / sqrt (2)

T  =   ( x^2  + x^2 - 148 + 5476 )^(1/2) / 2   +  ( x^2 + 3969)^(1/2) / sqrt (2)

T'     =   (1/4) ( 4x - 148)/ ( 2x^2 - 148x + 5476)^(1/2)  +  (2x) /[sqrt (2)(x^2 + 3969)^(1/2)]    = 0

       ( x - 37)                                   x

_____________________  +  ______________________     = 0  

(2x^2 - 148x + 5476)^(1/2)        sqrt (2) (x^2 + 3969)^(1/2)

Note  that  we  can write  the denomnator of the  first fraction as

2 ( x^2 - 74x + 2738)

So   we can write

(x - 37)                                                                    x

__________________________   +  _____________________   =   0

sqrt (2) ( x^2 - 74x + 2738)^(1/2)       sqrt (2) ( x^2 + 3969)^(1/2) 

(x - 37)                                                          -x

____________________    =              _________________           sqaure both sides

(x^2 - 74x + 2738)^(1/2)                        (x^2 + 3969)^(1/2) 

(x - 37)^2                                  x^2

_______________     =   ___________       cross-multiply

x^2 - 74x + 2738                x^2 + 3969 

(x - 37)^2 ( x^2 + 3969)  =   x^2 ( x^2 - 74x + 2738)     simplify

x^4 - 74 x^3 + 5338 x^2 - 293706 x + 5433561   =  x^4 - 74 x^3 + 2738 x^2

After a little manipulation we get

2600 x^2 - 293706 x + 5433561 = 0

Putting this into the quadratic formula  and  evaluating  we get  that  

x =   [ 293706   - sqrt  ( 293706^2  - 4*2600*5433561)]  / (5200)  =

[ 293706  -  sqrt ( 29754180036)  ]  / 5200  =

[ 293706  - 172494  ] /5200  =   23.31  / 100  =   23.31  = x

(There is another  value of x but it does not give us a minimum.......this is probably  due to the  fact that we squared the derivative )

Can you show me how you got those numbers?

I am still confused but I can understand more than before.

Hi Guest!

Is there perhaps a bit more context to the question?

=^._.^=

Hi mzhu23!

Chart

Let's make a chart where r is the number Rob has, s is the number of glue sticks Sydney has, and k is the number of glue sticks Koreb has at the beginning. 

Rob    Sydney    Koreb

r         s               k                 # Sydney gives Rob and Koreb as many glue sticks as each of them then has

2r       s - r - k      2k               # Koreb gives Sydney and Rob as many glue sticks as each has

4r       2(r - s - k)  3k - s - 2r

What do we know?

So from the graph what do we know. 

We know that: 

r + s + k = 48

4r = 16

2(s - r - k) = 16

3k - s - 2r = 16

Solving r

4r = 16

r = 4

Plugging r in past equations

4 + s + k = 48

s + k = 44 # New equation

2(s - r - k) = 16

s - r - k = 8

s - 4 - k = 8

s - k = 12 # New equation

3k - s - 2(4) = 16

3k - s = 24

Finding s and k

Two important equations from above are... s + k = 44 and s - k = 12. 

So, if we add them together, 2s = 56. 

s = 27. 

That would make k 15 (27 - 15 = 12)

Answer

Rob had 4 gluesticks. 

Sydney had 27 gluesticks. 

Koreb had 15 gluesticks. 

I hope this helped. :))))

=^._.^=

Note that with weights of 1,2,4   we can weigh out any  amount from  1 - 7 inclusive

And

1, 2, 4 , 8   lets us weigh out any  amt  from1-15

And

1,2,4,8,16   lets us weigh out  any amt from 1 - 31

And

1,2,4,8,16,31  lets us weight out any  amt  from 1 - 63

Note  that  8 pounds = 8 * 16  ounces  =  128  ounces

1,2,4,8,16,32,64   allows us to weigh out any amt  from 1 - 127  ounces

Yes I did see your solution as 23.31 is the value of x. I assume that it would have some rounding because of sqrt. I am trying to get to the value of x in terms of sqrt root so I do not make any approximations. Would calculus help with that? 

With calculus would it be d/dt(above function) -> 0? Could you please help with calculus

You have the correct Total Time function

We could use Calculus  to solve this but the  derivative is a little messy....I solved it  here  with a graph :

https://web2.0calc.com/questions/interesting-geometry

However...if you want me to, I  think I can solve it with pure Calculus.....

I have not looked for a general solution but the question implies that the ratio is always the same.

If you make ABCD a square and let P be the midpoint of AC then the solution is super easy to find.

I won't perform the  computations....but here is a way to tell

put (-6)  into the function  and evaluate

put (-5)  into the function and evaluate.....if the signs on the reults are different, then a zero occurs between these values

If you  have to  ...do  the  same  with   -5   and  -4 ,   -4 and - 3  and    -3, and  -2

If you  do this correctly, you should find that   -4  and  -3   is correct  !!!

False......the 2x^3  term determines the end behavior  on the left....as x becomes moroe and more negative.....the function becomes more and more negative  towards - inf

False....the 2 x^4 term  determines the end behavior on the  right of the  graph.....as x  becomes more and more positive,  becomes more and  more positive towards + inf

False  -9x^5   becomes more  positive as  x is more and more negative.....the limit  towards -inf  =  + inf

We have the form

y= asin (x + b)

The function is

y = -4sin( x+ pi/2)

The amplitude = l a l  =  l -4 l   = 4

Also.....The midline  is y = 0

The amplitude is the height of the curve  above the midline =  4

See the graph here :

https://www.desmos.com/calculator/o06yqc9wkk