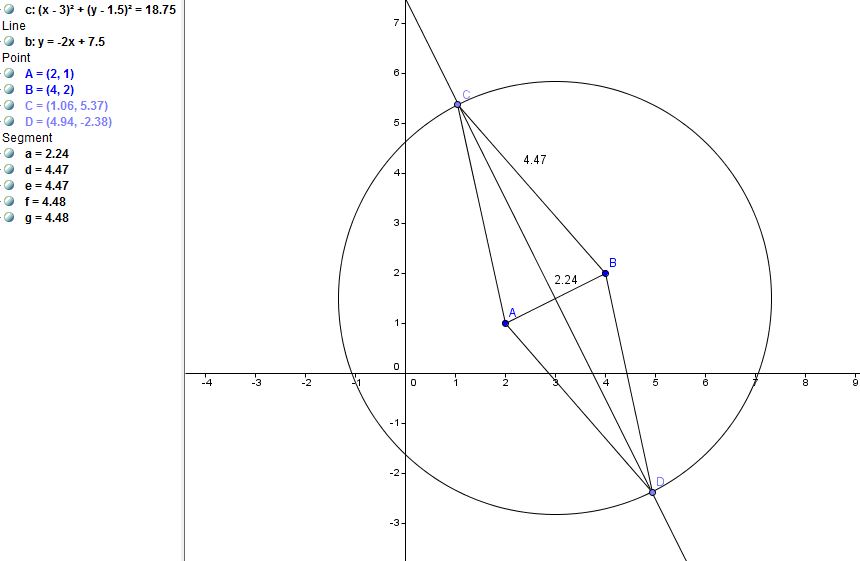
Given the two points A(2,1), and B(4,2) that forms the base of an isosceles triangle,
a. find the two points of the two isosceles triangles where the sides of each of the triangles are twice the length of the base.
b. If A=bh/2 for a triangle find the area of the isosceles triangle above.
____________________________________________________________
The second part is easier than the first
Let's first find the distance between these two points = sqrt [ (4-2)^2 + (2-1)^2] = sqrt(5)
Now....since the sides are twice the base...one of them must be 2sqrt(5)
So.....we can find the height of these triangles by the Pythagorean Theorem = sqrt (( 2sqrt 5)^2 - (sqrt(5)/2)^2 ) = sqrt [ 20 - 5/4 ] = sqrt [ 75 ]/2 = (5/2)sqrt (3) = 2.5sqrt (3)
So....the area of one of these triangles is (1/2)B * H =
(1/2) sqrt(5) * (5/2) sqrt (3) = (5/4)sqrt(15) sq units
For the first part......find the midpoint of AB = (3,1.5)
Construct a circle with a center of (3,1.5) and a radius of 2.5sqrt (3)
So the equation of this circle is (x - 3)^2 + ( y-1.5)^2 = 15
The slope of AB = (1/2)......so a line perpendicular to this which passes through the midpoint of AB will have the equation
y = (-2)(x - 3) + 1.5
y = -2x + 6 + 1.5
y = -2x + 7.5
Putting this into the equation of the circle for y, we have that
(x - 3)^2 + ( -2x + 7.5 -1.5)^2 = 18.75
(x - 3)^2 + ( -2x + 6)^2 = 18.75
(x -3)^2 + (6 - 2x)^2 = 18.75
x^2 - 6x + 9 + 36 - 24x + 4x^2 = 18.75
5x^2 - 30x + 26.25 = 0 divide through by 5
x^2 - 6x + 5.25 = 0
Solving this for x....we have that x ≈ 1.06 and x ≈ 4.94
So.......the associated y values for these two points are
y = - 2[ 1.06 ] + 7.5 ≈ 5.38
y = -2 [ 4.94] + 7.5 ≈ 2.38
So.....the two points where the sides of both isosceles triangles intersect are
(1.06, 5.38 ) and ( 4.94, 2.38)
Here's a graph :