All Answers 352711 Answers

First find  g(5)  by putting in 5 for x  

5(-5) + 2 (-5)^2 = -25 + 50 = 25

then put 25 in f(x)

3 - sqrt(25) = 3 - 5 = -2      (it COULD be  (3 - -5) = 8    because sqrt 25 is +-5 )   

nvm my mistake was found, it is -2

In the sequence:
each term (starting from the third term) is the product of the two terms before it.

For example, the seventh term is 256, which is the product of the fifth term (8) and the sixth term (32).

This sequence can be continued forever, though the numbers very quickly grow enormous! (For example, the 14th term is close to some estimates of the number of particles in the observable universe.)

What is the last digit of the 35th term of the sequence?

\(1,2,2,4,8,32,256,\ldots,\)

\(\begin{array}{|rcl|l|} \hline a_n &&& \text{Fibonacci numbers} \\ \hline a_1 &=& 2^{0} & F_{0} = 0 \\ a_2 &=& 2^{1} & F_{1} = 1 \\ a_3 &=& 2^{1} & F_{2} = 1 \\ a_4 &=& 2^{2} & F_{3} = 2 \\ a_5 &=& 2^{3} & F_{4} = 3 \\ a_6 &=& 2^{5} & F_{5} = 5 \\ a_7 &=& 2^{8} & F_{6} = 8 \\ a_8 &=& 2^{13} & F_{7} = 13 \\ a_9 &=& 2^{21} & F_{8} = 21 \\ \ldots \\ a_n &=& 2^{F_{n-1}} \\ \hline a_{35} &=& 2^{F_{34}} & F_{34} = 5702887 \\ \mathbf{a_{35}} &=& \mathbf{2^{5702887}} \\ \hline \end{array} \)

The last digit of the 35th term of the sequence is \( \mathbf{2^{5702887}} \pmod{10}\)

\(\begin{array}{|rcll|} \hline && \mathbf{2^{5702887}} \pmod{10} \quad &| \quad \mathbf{2^4}=16 \equiv \mathbf{6} \pmod{10} \\ &\equiv & 2^{4*1425721+3} \pmod{10} \\ &\equiv & \left( 2^{4} \right)^{1425721}*2^3 \pmod{10} \\ &\equiv & 6^{1425721}*2^3 \pmod{10} \quad & | \quad 6^n \equiv 6 \pmod{10} \\ &\equiv & 6 *2^3 \pmod{10} \\ &\equiv & 6 *8 \pmod{10} \\ &\equiv & 48 \pmod{10} \\ &\equiv & \mathbf{8} \pmod{10} \\ \hline \end{array} \)

The last digit of the 35th term of the sequence is 8

What is the smallest integer n, greater than 1, such that \(n^{-1}\pmod{1320} \)is defined?

According to Euler's theorem, if a is coprime to m, that is, gcd(a, m) = 1, then
   \({\displaystyle a^{\phi (m)}\equiv 1{\pmod {m}},}\)
where  \( {\displaystyle \phi }\)   is Euler's totient function.  
A modular multiplicative inverse can be found directly:
  \( {\displaystyle a^{\phi (m)-1}\equiv a^{-1}{\pmod {m}}.}\)
n must be coprime to 1320 or gcd(n,1320) = 1,

Factorization of 1320:

\(1320 = 2^3×3×5×11\) (6 prime factors, 4 distinct)

The smallest integer n > 1 coprime to 1320 is 7.

\(\begin{array}{|rcll|} \hline && 7^{-1}{\pmod {1320}} \\ &\equiv& 7^{\phi (1320)-1}{\pmod {1320}} \quad | \quad \phi (1320) = 320 \\ &\equiv& 7^{320-1}{\pmod {1320}} \\ &\equiv& 7^{319}{\pmod {1320}} \\ &\equiv& \mathbf{943} {\pmod {1320}} \\ \hline \end{array}\)

I see.

I was referring to the sequence 1, 1/2, 1/3,...

Every single one of its terms is strictly positive but the limit is 0 (which is not strictly positive)

Ok.  To what were you referring?  (I misread your earlier reply as the sum of the natural numbers!).

Alan I am sorry but this is not what I was referring to 

Isn't 14 a factor of 14 too?

Hectictar,

Guest #2 is referring to a situation that occurs in the context of the analytic continuation of the Zeta function (see https://www.youtube.com/watch?v=YuIIjLr6vUA).  However, I doubt that that context is relevant for the questioner here!

any rational roots are a factor of the constant term divided by a factor of the coefficient of the highest degree term.

here the constant term is -14 with factors +/- 1, +/- 2, +/- 7 +/- 14

and the leading coefficient is 7 with factors +/- 1, +/- 7

thus we have possible rational roots

+/- 1/7

+/- 2/7

+/- 1

+/- 2

+/- 7

+/- 14

a total of 12 possible rational roots

As follows:

(Because this is the Rydberg equation only the positive square root makes sense)

the number of popcorn pieces in a bag of small popcorn sold at a given movie theater y/n

yes

the heights of all the people on a field trip that is made up of first-graders and their teachers y/n

no

the values of the coins collected from a parking meter y/n

no

the heights of the players in a basketball league y/n

yes

Guest, how can a sum of positive numbers ever be not positive??

Yes ok   

I don't think you umderstood the question. The guest is not asking for the maximal amount of rational roots the polynomial can have.

(ii)  False

As a counterexample,

Let     f(x)  =  x - 4     and     a  =  0     and     b  =  6

\(\int_{a}^{b}f(x)\,dx\,=\,\int_{0}^{6}(x-4)\,dx\,=\,(\frac{x^2}{2}-4x)\Big|_{0}^{6}\,=\,-6\,<\,0\)

But....  5  is an element of the interval  [0, 6]  and

\(f(5)\,=\,5-4\,=\,1\nless0\)

The integral is negative because the triangle under the x-axis is bigger than the triangle above the x-axis,

but not all the values of  f(x)  are negative for  x  in the interval  [0, 6] .

I might be simplifying this too much but there can only be a maximum of 4 becasue 4 is the degree.

Maybe there is less than 4

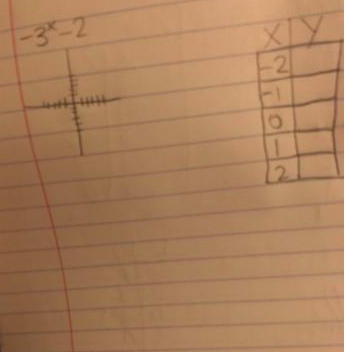
\(y\,=\,-3^x-2\)

When     \(x=-2\) ,     \(y\,=\,-3^{-2}-2\,=\,-\frac19-2\,=\,-\frac19-\frac{18}{9}\,=\,-\frac{19}{9}\)

When     \(x=-1\) ,     \(y\,=\,-3^{-1}-2\,=\,-\frac19-2\,=\,-\frac13-\frac{6}{3}\,=\,-\frac{7}{3}\)

When     \(x=\phantom{-}0\) ,     \(y\,=\,-3^0-2\,=\,-1-2\,=\,-3\)

When     \(x=\phantom{-}1\) ,     \(y\,=\,-3^1-2\,=\,-3-2\,=\,-5\)

Can you find what  y  equals when  x  is  2 ?

Multiply each term in the first set of parenthesees by each term in the second set of parenthesees and add the products together. It's "first times first plus first times second plus second times first plus second times second"

(a + b)(c + d)   =   ac  +  ad  +  bc  +  bd

So.....

(8x² + -9)(2x + 4)   =   . . .?

Do you see what to do next? If you still don't understand please say so

See here :

https://web2.0calc.com/questions/help_88019

F  =  multiply the first term in each set of parentheses together

This gives us  5xy^2 * xy^2  =  5x^2y^4

O =   multiply  the " outside terms" together

This gives us  5xy^2 * (-4)  =  -20xy^2

I = multiply the "inside  terms" together

This gives us   1 * xy^2  =  xy^2

L  =  multiply the last term in each set of parentheses together

This gives us  (+1) (-4)  =  - 4

So....combining the terms we get

5x^2y^4 - 20xy^2 + xy^2 - 4  =

5x^2y^4 - 19xy^2 - 4

I don't know how to solve such a problem mathematically. I will leave it to one of the mathematicians to shed some light on it. However, it is a trivial matter to write a very short computer code to find the solution(s) almost intantaneously
a=20000; b=1;c= (a+b)^2 - a^2; if(c==10!, goto4, goto5);printc, a, b; a++;if(a<25000, goto2, 0);a=20000;b++;if(b<100, goto2, discard=0;
As it turns out, you have more than one solution! In fact, there are 4 sets of solutions as follows:
(a + b)^2 - a^2 = 10!
a = 1,814,400/b - b/2 
   a           b
 22640     80 =(22,640 + 80)^2 - 22,640^2 =10!
 21558     84 =(21,558 + 84)^2 - 21,558^2 =10!
 20115     90 =(20,115 + 90)^2 - 20,115^2 =10!
 18852     96 =(18,852 + 96)^2 - 18,852^2 =10!

27.

K  =  area of triangle  =  \(\frac12\) ( base )( height )

Let the base  =  a

and the height  =  c sin B

Let's get  c  in terms of what we know using the Law of Sines

\(\frac{c}{\sin C}\,=\,\frac{a}{\sin A}\\~\\ c\,=\,\frac{a\sin C}{\sin A}\)

So the height  =  c sin B  =  (\(\frac{a\sin C}{\sin A}\)) sin B  =  \(\frac{a\sin B\sin C}{\sin A}\)

K  =  area of triangle  =  \(\frac12\) ( base )( height )  =  \(\frac12\) ( a )( \(\frac{a\sin B\sin C}{\sin A}\) )   =   \(\frac{a^2\sin B\sin C}{2\sin A}\)

\(K\,=\,\frac{a^2\sin B\sin C}{2\sin A}\)