s(t) = t3 - 6t2 + 9t + 1
a:
v(t) = s'(t) because velocity is the derivative of position
v(t) = 3t2 - 12t + 9 This equation tells us her velocity at any time t . To find her velocity when t = 3 , plug in 3 for t
v(3) = 3(3)2 - 12(3) + 9
v(3) = 0 (This is is meters per second)
b:
a(t) = v'(t) because acceleration is the derivative of velocity
a(t) = 6t - 12 Now we can find what value of t causes a(t) to be 0
6t - 12 = 0 Solve this equation for t
t = 2
So when t = 2 her acceleration is 0 . But we want to know what is her velocity when t = 2 ?
v(2) = 3(2)2 - 12(2) + 9
v(2) = -3 (This is in meters per second)
c:
Alice is at rest when her velocity is zero. Can you find what values of t make v(t) be 0 ?
d:
She's going backwards when her velocity is negative. So after finding what values of t make her velocity 0 , we can test a t value on each side of each zero to find the intervals where the velocity is negative.
e:
Here's a graph of s(t) with points on the graph labeled for t = 1,2,3,4,5,6 :
https://www.desmos.com/calculator/ryywlaotbp
I'm kind of guessing on this one, but here's my guess:
After 0 s , she is 1 m from the starting position, and she moved a total distance of 0 m
After 1 s , she is 5 m from the starting position, and she moved a total distance of 4 m
After 2 s , she is 3 m from the starting position, and she moved a total distance of 6 m
After 3 s , she is 1 m from the starting position, and she moved a total distance of 8 m
After 4 s , she is 5 m from the starting position, and she moved a total distance of 12 m
After 5 s , she is 21 m from the starting position, and she moved a total distance of 28 m
After 6 s , she is 55 m from the starting position, and she moved a total distance of 62 m
Let us know if you have a question or need more help on this ![]()
Golf-course designers have become concerned that old courses are becoming obsolete since new technology has given golfers the ability to hit the ball so far. Designers, therefore, have proposed that new golf courses need to be built expecting that the average golfer can hit the ball more than 255 yards on average. Suppose a random sample of 166 golfers be chosen so that their mean driving distance is 259.5 yards, with a standard deviation of 44. Conduct a hypothesis test where H0:μ=255 and H1:μ>255 by computing the following: (a) test statistic (b) p-value p= (c) If this was a two-tailed test, then the p-value is
\(\mu=255\\ n=166\\ \bar X=259.5\\ S=44\\ Test \;Stat \;is \;Z\\ Z=\frac{\bar X-\mu}{\left( \frac{S}{\sqrt n} \right)}\\ Z=\frac{259.5-255}{\left( \frac{44}{\sqrt {166}} \right)}\\ Z=1.318\\ \\~\\ H_0:\quad \mu=255\\ H_A:\quad \mu>2.55\\ \\~\\ P(Z>1.318) =P(Z<-1.38) \qquad \text{You can use either}\)
Maybe you have to use a given table.
I like this site.
http://davidmlane.com/hyperstat/z_table.html
\(\boxed{\bf\text {It gives the P value as 0.0938}}\)
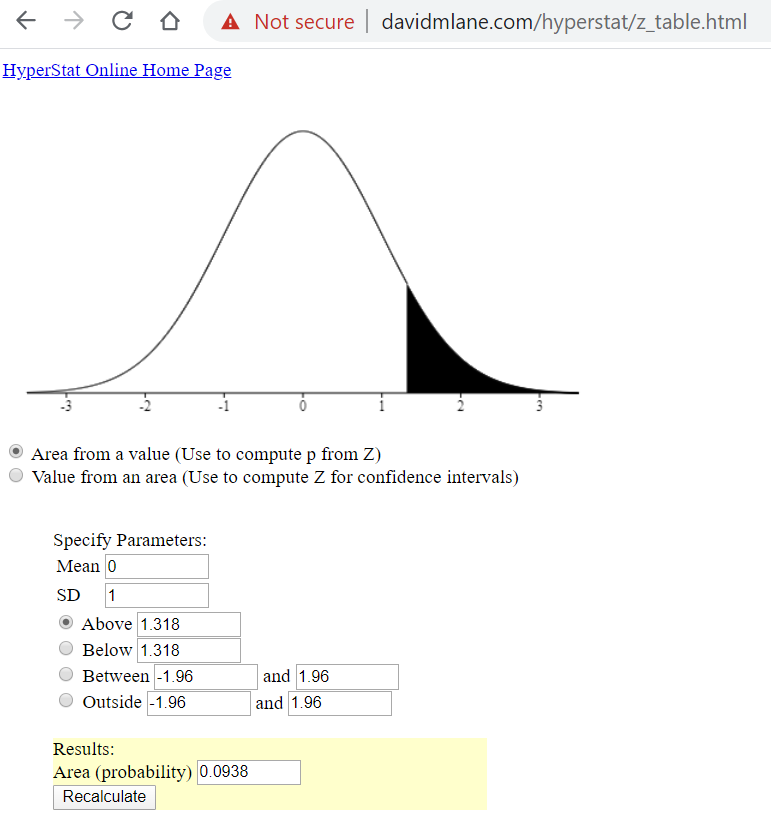
I am reasonably sure that is all correct.
Coding
\mu=255\\
n=166\\
\bar X=259.5\\
S=44\\
Test \;Stat \;is \;Z\\
Z=\frac{\bar X-\mu}{\left( \frac{S}{\sqrt n} \right)}\\
Z=\frac{259.5-255}{\left( \frac{44}{\sqrt {166}} \right)}\\
Z=1.318\\
\\~\\
H_0:\quad \mu=255\\
H_A:\quad \mu>2.55\\
\\~\\
P(Z>1.318)
=P(Z<-1.38)