All Answers 358181 Answers

Count the number of full blue squares. To this number add half the number of half-filled blue squares. Divide the result by 100 to get the fraction occupied by the blue squares (then multiply by 100 to get the percentage).

Find the smallest positive integer n such that 135n is divisible by 360.

\(\begin{array}{|rcll|} \hline \text{lcm}(360,135) &=& 1080 \\ 135n &=& 1080 \\ n &=& \dfrac{1080}{135} \\ \mathbf{n} &=& \mathbf{8} \\ \hline \end{array}\)

If xy = 7 and x + y = 5, then find \(x^3 + y^3\).

1.

\(\begin{array}{|rcll|} \hline (x + y)^2 &=& x^2+2xy+y^2 \\ 5^2 &=& x^2+2*7+y^2 \\ x^2+y^2 &=& 25-14 \\ \mathbf{x^2+y^2} &=& \mathbf{11} \\ \hline \end{array}\)

2.

\(\begin{array}{|rcll|} \hline (x^2+y^2)(x+y) &=& x^3+x^2y+y^2x+y^3 \\ 11*5 &=& x^3+y^3+xy(x+y) \\ 55 &=& x^3+y^3+7*5 \\ x^3+y^3 &=& 55 -35 \\ \mathbf{x^3+y^3} &=& \mathbf{20} \\ \hline \end{array}\)

Solve for x:
\(\large \dfrac{\color{red}{ \sqrt{2x-1} }+\color{green}{\sqrt{2x+1}} }{\color{green}{ \sqrt{2x+1}}-\color{red}{\sqrt{2x-1}} }=\color{blue}{\dfrac{5}{3}} \quad, \quad \color{magenta}{x} = \ ?\)

\(\begin{array}{|rcll|} \hline \dfrac{\color{red}{ \sqrt{2x-1} }+\color{green}{\sqrt{2x+1}} }{\color{green}{ \sqrt{2x+1}}-\color{red}{\sqrt{2x-1}} } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ \color{red}{ \Big(\sqrt{2x-1} }+\color{green}{\sqrt{2x+1}} \Big)} { \color{green}{ \Big( \sqrt{2x+1}}-\color{red}{\sqrt{2x-1}} \Big) } * \dfrac{ \Big( \sqrt{2x-1}+ \sqrt{2x+1} \Big)} { \Big( \sqrt{2x+1}+ \sqrt{2x-1} \Big) } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ \Big( \sqrt{2x-1}+ \sqrt{2x+1} \Big)^2} { 2x+1-(2x-1) } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ 2x-1 +2\sqrt{(2x-1)(2x+1)}+2x+1 } { 2x+1-(2x-1) } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ 4x +2\sqrt{(2x-1)(2x+1)} } { 2x+1-2x+1 } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ 4x +2\sqrt{(2x-1)(2x+1)} } { 2 } &=& \color{blue}{\dfrac{5}{3}} \\\\ \dfrac{ 4x +2\sqrt{4x^2-1} } { 2 } &=& \color{blue}{\dfrac{5}{3}} \\\\ 2x +\sqrt{4x^2-1} &=& \color{blue}{\dfrac{5}{3}} \\\\ \sqrt{4x^2-1} &=& \color{blue}{\dfrac{5}{3}} - 2x \quad | \quad \text{square both sides} \\\\ 4x^2-1 &=& \left( \color{blue}{\dfrac{5}{3}} - 2x\right)^2 \\\\ 4x^2-1 &=& \dfrac{25}{9}-\dfrac{20x}{3} + 4x^2 \\\\ -1 &=& \dfrac{25}{9}-\dfrac{20x}{3} \\\\ \dfrac{20x}{3} &=& \dfrac{25}{9} + 1 \\\\ \dfrac{20x}{3} &=& \dfrac{34}{9} \\\\ x &=& \dfrac{34}{9}* \dfrac{3}{20} \\\\ x &=& \dfrac{17}{3*10} \\\\ \mathbf{x} &=& \mathbf{\dfrac{17}{30}} \\ \hline \end{array}\)

See the following  image  :

Let O = (0,0)

Let A = (2,0)

Let B = (0,2)

Let E = (-2,0)

C =(0,1)

Note that BE  is the diameter  = 4

And  CE  = BE - BC  = 4 - 1  =   3

Since AOB is right  with OA =  2   and  OC =  1

Then, by the Pythagorean Theorem  AC  =sqrt  ( OA^2  + OC^2)  = sqrt  ( 2^2 + 1^2)  =  sqrt (5)

By the intersecting chord theorem  we  have that

BC * CE  =  AC * CD

1 * 3  =  sqrt (5) * CD

3 = sqrt (5) * CD

CD =  3/sqrt (5)  ≈  1.34

thanks, I should probably find another forum XD

lmao wish i could help u but im going into 8th grade :(

good luck in high school tho!

Graphing the possible values for \(a>b\) as positive integers. (Selected Points are the possible values)

_____________________________________________________________

a is y-axis

b is x-axis

By plugging in values of A and B...

Notice how if we set b = 1, we can get an infinite series as \(a\) increases by increments of 1.

Notice how if we set b = 2, we can get the same thing except the starting term is different.

So the answer really is the sum of an infinite series of infinite series'.... very interesting!

_____________________________________________________________

Let us find the infinite series if b = 1 and \(a\) increases to start off:

\(\frac{1}{20}+\frac{1}{40}+\frac{1}{80}...\)

_____________________________________________________________

The formula for an infinite series is

\(\frac{a_{(1)}}{1-r}\)

_____________________________________________________________

So the series for b = 1 is \(\frac{1}{10}\).

By applying the same method, we know that the series for b = 2, b = 3, b = 4 is:

1/100

1/1000

1/10000

respectively...

So now we have to find the sum to THAT infinite series, which is:

\(\frac{\frac{1}{10}}{1-\frac{1}{10}} = \boxed{\text{math is fun}}\)

*an interesting thing is as you add the number of different variables, the higher dimensions the graph is. Interesting how we don't need to actually VISUALIZE higher dimensional graphs, we can just calculate the sum if you have the method down.

THX!!!!!

A = (3,6)     B  = (-5,2)    C  = (7, -8)

Midpoint of  BC = [ (7 - 5) / 2 , (-8 + 2)  / 2)   = ( 2/2   , -6/2)   = (1, -3)  = D

Slope  of  line through  AD  = [ 6- - 3 ]  /  [ 3 - 1 ] =  9/2

Equation of line   through AD  ...   y = (9/2) ( x -3) + 6  ......y = (9/2) x - 27/2 + 6  ......y = (9/2)x  - 15/2

Midpoint of  AC =  [ (3 + 7)/2  , (-8 + 6))/2  ]  =  (10/2, -2/2)  =  ( 5, -1)  =  E

Slope of line through  BE  =  [ -1 - 2 ] / [ 5 - -5]  =  -3/10

Equation of line  through  BE....y=  (-3/10) ( x-5) - 1 ......y = (-3/10)x + 15/10 - 1  .....y = (-3/10)x + 1/2

Now we can find  the x intersection of these mediians by setting the equations of these lines equal

(9/2) x - 15/2  =  (-3/10)x + 1/2

(9/2  + 3/10) x  =  (1/2  + 15/2)

(24/5)x = 8 

x = 8 (5/24)  =  40/24  =  5/3

And the y coordinate of the  intersection of these medians  is

y = (-3/10)(5/3) + 1/2  =  0

So.....the  intersection of these medians =  (5/3 , 0)=  G

Now....the midpoint of  AB  = [(-5+ 3)/2, (2+6)/2) ]  = (-2/2, 8/2)  = (-1,4)  = F

And ths slope thruogh FC  = [ -8- 4]/ [7-  - 1] =  [ -12/8]  = -3/2

So the equation of the  line  through  FC  .....y = (-3/2) (x - -1) + 4.....y = (-3/2)x - 3/2 + 4....y = (-3/2)x +5/2

So...to prove  that   G  is on this line...let  x = (5/3)

So  when x  =(5/3)  then y  = (-3/2)(5/3) + 5/2  =  -5/2 + 5/2  =   0

So   ( 5/3 , 0)  is on FC  whivh proves that all therr medians intersect at G = (5/3, 0)

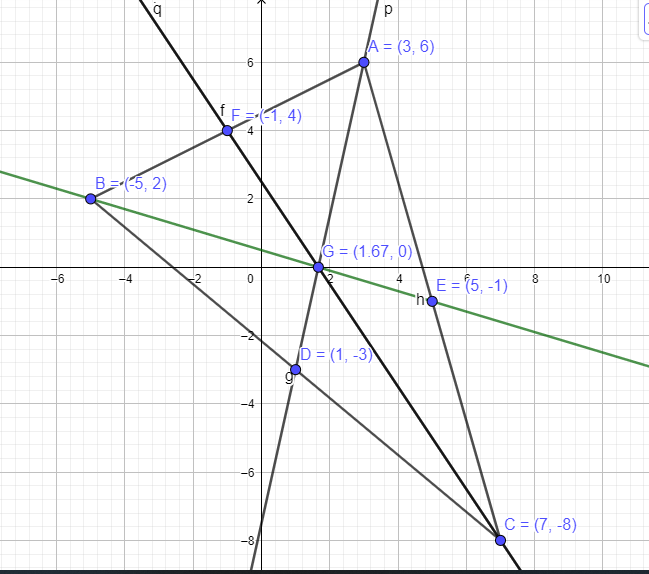
Here's a pic :

Hint:

Set the length of the grey rectangle to X

Set the width of the grey rectangle to Y.

Use simple algebra to find the other rectangle's width and length in terms of X and Y.

Then solve an equation.

good job

Yay I'm back after months of video games and coding.

What DOESN'T appear one time? We can call that being "deleted".
__________________________________________________________________

Let's call a term in list A "\(n\)"

 - \(n\) is only deleted if \(n\text{ }mod\text{ }4=3 \) and not \(n + 1\text{ }mod\text{ }8=7\)

so in other words, if \(n\) is a multiple of 3 and \(n+1\) is NOT a multiple of 7, then it shall be deleted.

Example {n = 3}

 - n is multiple of 3

 - n + 1 is NOT multiple of 7

therefore it should be deleted.

__________________________________________________________________

Now let us calculate how much will be deleted.

There are floor(1000/3) = 333 multiples of 3 from 1 - 1000.

There are floor(333/7) = 47 multiples of 7 that are also a multiple of 3.

That means there are 333 - 47 = 286 multiples of 3 that are NOT multiples of 7. That means 286 should be deleted.

__________________________________________________________________

Since the question asks how many numbers are not deleted in list C, we can easily find that the answer is 1000 - 286 is \(\boxed{714}\).

Please correct me if I am wrong.

Nevermind, I solved it!

Let the amount of peanut oil =  x quarts

Then the amount of olive oil  = (1.3  - x)  quarts

Then we can solve this equation

.19x  + .71 ( 1.3 - x)   = .39 ( 1.3)        simplify

.19x + .923 - .71x  = .507

(.19x  - 71x)  =  .507 - .923

-.52x  = -.416     divide both sides  by  -.52

x   =  .8   (quarts  of peanut oil used)

Welcome back CPhill!!!!!!!

The perimeter  is given by :

2* radius  + arc lengrh of the  sector  =

2r   +  r* theta      where  theta  is the measure  of the central  angle of the sector ( in radians)

So   we  have  that

38  =  2r  + r * theta     simplify

38 = r ( 2 + theta)    subbing   in for the radius  we  have that

38 = 9 (2 + theta)    divide both sides by  9

(38/9)  = 2 + theta     subtract 2 from both sides

20/9 =  theta  

The area of  the sector =   (1/2)* r^2 * theta

So....the area  =    (1/2) (9)^2  * ( 20/9)  =   (1/2) ( 9) (20)  =   90 cm^2

The horizontal leg of a dark blue triangle is 12, and the other leg is  12 * arctan(12/16)  

The sum of the first  n  even numbers   =    n ( n + 1)  

We have 250  even numbers  from  2 to 500  inclusive  

So....the sum of these  = 250 * 251   =  62750      (1)

The  sum  of the  even numbers from  2 to 8 inclusive  =  the sum of the first four even numbers =  4 * 5  = 20  (2)

So....the sum of the even numbers  between 10 and 500 inclusive  =  (1)  - (2)  =  

62750 -  20   =

62730

In a zoo, the ratio of giraffes to apes is 6 to 5 and the ratio of apes to zebras is 4 to 1. What is the minimum number of zebras the zoo could have?

The ratio of giraffes to zebras is NOT  6 : 1;   it's  6 : 1.25

The minimum number of zebras is 5

24 giraffes,   20  apes,   and  5  zebras

This ratio is:     6  :   5   :   1.25     

umm actually i think the gcd of 36 and 104 is 4.

gwenspooner did the prime factorization right, but what she missed is that 3^2 is not a factor of 104. so, the gcd is 2^2=4.

From A to B, the distance is 200. The time taken is 200/40=5 hours. From B to A, the distance is also 200. The time taken is 200/60=10/3 hours. The average speed is total distance/total time.

200+200/(5+10/3)

=400/(25/3)

=1200/25

=48 kph

All numbers that fall under this category can be described as 5n+3, where n is a number. 

The smallest 3 digit number that fits in the expression 5n+3 is 103. The greatest is 998. The list of these numbers is 103, 108, 111, ...998. The number of numbers in this list is (998-103)/5+1=895/5+1=179+1=180.

We find the prime factorization of 36 and 104 first. 

36: 2^2*3^2

104: 2^3*13.

Then the gcd must be 2^2*3^2, which is 36.