All Answers 356371 Answers

Factoring of 1000! gives:

1000!= 2^994 * 3^498 * 5^249 * 7^164 * 11^98 * 13^81 * 17^61 * 19^54 * 23^44 * 29^35 * 31^33 * 37^27 * 41^24 * 43^23 * 47^21 * 53^18 * 59^16 * 61^16 * 67^14 * 71^14 * 73^13 * 79^12 * 83^12 * 89^11 * 97^10 * 101^9 * 103^9 * 107^9 * 109^9 * 113^8 * 127^7 * 131^7 * 137^7 * 139^7 * 149^6 * 151^6 * 157^6 * 163^6 * 167^5 * 173^5 * 179^5 * 181^5 * 191^5 * 193^5 * 197^5 * 199^5 * 211^4 * 223^4 * 227^4 * 229^4 * 233^4 * 239^4 * 241^4 * 251^3 * 257^3 * 263^3 * 269^3 * 271^3 * 277^3 * 281^3 * 283^3 * 293^3 * 307^3 * 311^3 * 313^3 * 317^3 * 331^3 * 337^2 * 347^2 * 349^2 * 353^2 * 359^2 * 367^2 * 373^2 * 379^2 * 383^2 * 389^2 * 397^2 * 401^2 * 409^2 * 419^2 * 421^2 * 431^2 * 433^2 * 439^2 * 443^2 * 449^2 * 457^2 * 461^2 * 463^2 * 467^2 * 479^2 * 487^2 * 491^2 * 499^2 * 503 * 509 * 521 * 523 * 541 * 547 * 557 * 563 * 569 * 571 * 577 * 587 * 593 * 599 * 601 * 607 * 613 * 617 * 619 * 631 * 641 * 643 * 647 * 653 * 659 * 661 * 673 * 677 * 683 * 691 * 701 * 709 * 719 * 727 * 733 * 739 * 743 * 751 * 757 * 761 * 769 * 773 * 787 * 797 * 809 * 811 * 821 * 823 * 827 * 829 * 839 * 853 * 857 * 859 * 863 * 877 * 881 * 883 * 887 * 907 * 911 * 919 * 929 * 937 * 941 * 947 * 953 * 967 * 971 * 977 * 983 * 991 * 997

1000/7 = 142.8571428571428571      floor = 142

flor(142/7) = 20

floor(20/7)=2

So I think  142+20+2=164

This is the same as the other two answers.

(afton just made a careles sum error at the end)

Here's (b)....it's pretty much an extension of (a)

1000/7 = 142 numbers that have at least 1 factor of 7

1000/49 = 20 numbers that have at  an additional factor of 7

1000/343 =  2 numbers that have a third factor of 7

So.........    142 + 20 + 1 =  163

And 7^163 will divide 1000!   ...so n = 163

The question as written leads to a complex value for AD!!!!  Hoever, if BD/CD = 2:5 then AD has a more sensible value (=8).

"If f(4) = 1 and f(2x) = 3f(x) for all x, then find f(64)."

Start with 

 \(a^2\; \propto \;\frac{1}{b^2}\\ a^2\; = \;\frac{k}{b^2}\)

Now sub in a=7 and b=4 to get k.

Then you have the formula that you can use for any given value of a or b.

Find all real x where
2*(x - 5)/(x - 4) > (2x - 5)/(x + 2) + 5.
Give your answer in interval notation.

Hello Guest!

\(2\cdot (x - 5)/(x - 4) > (2x - 5)/(x + 2) + 5.\)

\(x_1<0\\ x_2>3.4\\x_3=4\)      | Arndt Brünner

\((2\cdot (x - 5)/(x - 4) > (2x - 5)/(x + 2) + 5)\)

                                               \(\color{blue}|x\in\mathbb Q\ ;x<0\ and\ 3.4< x< 4\)

  !

Hi yelliah and Asinus,

You are both very welcome.

I have improved the graph just a little.

If you need me to explain something in particular then just ask, I will do my best to help you further.

And yes Asinus, I do know your name but I do not usually use real names publically unless I am invited to do so. 

(Or unless I am being very absent minded     )

Usernames are for public use.   

Hint:  use a right-angled triangle with legs of 20 and 25

The set of all solutions of the system

Hello Guest!

1)

\(1)\\ y <= 4\\ 2x + y >= 5\\ 2)\ x >= 0\\ 3)\ y >= 0 \)

1)

\(x + y \le 4 \)             \(1+3\le4\)

\(2x+y\ge 5\)           \(2\cdot1+3\ge 5\)

\(y=4-x\\ y=5-2x\\ 4-x=5-2x\\ 2x-x=5-4\)

\(x=1\\ y=3\)

2)

\(x \ge 0 \)

\(x\in| \mathbb {Q}|\)

3)

\(y\ge 0 \)

\(y\in| \mathbb {Q}|\)

  !

If f(x) = x^3 + 1, find f^{-1}(2010).

Hello Guest!

\(f(x)=x^3+1\\ f^{-1}(2010)=?\)

\(f(2010)=2010^3+1\)

\(f^{-1}(2010)= \frac{1}{2010^3+1}\)

\(f^{-1}(2010)=1.23143594899\times 10^{-10}\)

  !

a² + b² = c²

a² + b² = 10²

a² + b² = 17²

Using the info that it is a 3:5 ratio, you can determine that the maximium numbers it can be is 6:10 without being 10.

All other 3:5 ratios under 10 not using decimals are 3:5, since that would give AD = 16.7 and 8.6 which don't match up, so it isn't a whole number.

Next I used a simultaneus equation: 289 - y = 100 - x    and    3y = 5x.

What I got was x = 567/2 or 283.5 and y = 945/2 or 472.5

Squaring them gave me the answer: x = 16.8 and y = 21.7 which still didn't make sense.

So then I thought about it and it's impossible.

Hi Melody,

Thank you so much for helping me. I under stand so much now!

                 280 x^3*y*z^4

"I will try again. "   

Forgive me Melody, you know my name.
The "a" confused me a bit.
Thank you very much for your detailed description of how to solve this question.

  !

\(g(x)=\int \frac{-1}{2x}\;dx\\~\\ g(x)=\frac{-1}{2}\int \frac{1}{x}\;dx\\~\\ g(x)=\frac{-1}{2}*lnx+c\\ g(x)=\frac{-lnx}{2}+c \)

I just lost a full post on this, I will try again.    

Hi Asinus and yellah,

Let f(x) and g(x) be functions with domain (0,infinity). Suppose f(x)=x^2 and the tangent line to f(x) at x=a is perpendicular to the tangent line to g(x) at x=a for all positive real numbers a. Find all possible functions g(x).

\(\int \frac{1}{x}dx=lnx+c \qquad NOT\qquad \int \frac{1}{x}dx=ln|x|+c\)

BUT   x must be in the domain of positive real numbers.

That is why the question specifically states that it is referring only to real positive values of x,

The introduction of the letter 'a' is confusing but all it is saying is that the tangent of f(x) will be perpendicular to the tangent g(x) is true at any specific value of x which is greater than 0.

'a' is used to indicate any specific constant of your choice.

So we have

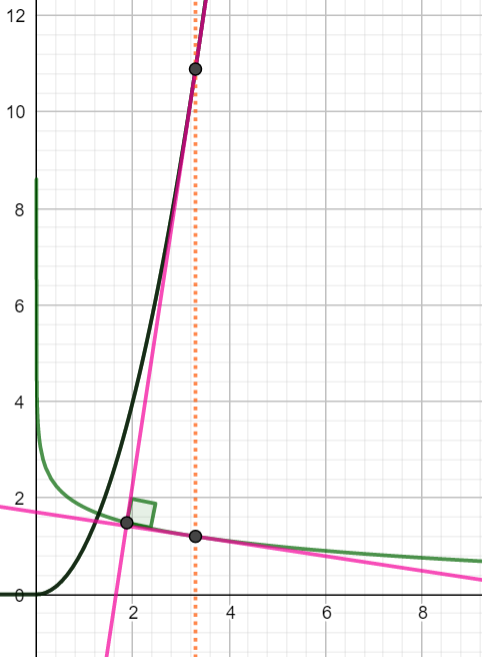
\(f(x)=x^2\\ g(x)=\frac{-1}{2}\;lnx +c\)

Here is a graph to show this.  You can change the values of a and c with the sliders.

Thanks guests and Alan    

[1000 / 7  +  1000 / 7^2  +  1000 / 7^3] =142 +  20  + 2 = 164 [Take the integer part only].

So, the largest n = 164 

This question is about an ant, and there's a comment by Pangolin. 

How many of you knew that a pangolin is ... wait for it ... an anteater!  

What I meant by 50-50 is that, if the ant is allowed to move either direction, then for each step, there'd be just as much chance that he would go backward as forward, therefore his probability of landing where he started would be 50%. 

_.

Correct for both! Great job!

As follows

To find how long the ball ia bove 80 m set h = 80 and solve for t.

To find how long it is in the air set h = 0 and solve for t.

In both cases there will be two values for t, only one of which will make sense in the context of the question.

Like so