All Answers 356710 Answers

AS  and  BS   form  legs  of  a right triangle  and  each  = 200  yds

So AB   =   sqrt  (200^2  + 200^2)  =  sqrt (200^2  * 2)   =  200sqrt (2)   { yds }  ≈ 282.8 (yds}

What I have gotten so far is that it will be $5 and something cents for each ticket.I tried my best to get the right answer but I keep getting different answers. I hope this helps.

Rearrange  the  first equation as   y  =  -3x +  8

Rearrange  the second equation  as   y = (2/b)x  + 9/b

Slope  of  first line = -3

Slope of a perp  line =  1/3

So  

1/3 =  2/b     cross-multiply

b  = 3*2

b  = 6

The distance  is  just  the hypotenuse of  a  right triangle   with legs of  5  and  12....so...

distance = sqrt  [5^2  + 12^2]    =  sqrt  [169 ]   =  13  miles

OBJD  is close....but....we  need  to add 1 to each exponent and then take that product....so..

(4+1)  (3+1) (2 + 1) ( 2 + 1)   =

5  *  4    *   3    *    3       =

180     factors

Sorry, I do not understand. Could you keep explain? Sorry if I am just being dumb.

Sorry, but that is wrong.

Since this is an AoPS question, I'll give you a start-up but not the whole solution.

Here, we would use permutations. However, what will be different from the regular question, is one person can hold two positions.

(-6, 13)  (2,9)  are on  K

Slope of K    =  (13-9)  /( -6 - 2)  =  4 / -8   =  -1/2

Equation of  K  is

y =(-1/2) ( x -2)  + 9

y  = (-1/2) x + 1  + 9

y  = (-1/2) x  +  10 

Set  L  = K

2x -10   =(-1/2)x  + 10

2x  + (1/2) x  = 10  + 10

(5/2)x    =20

x = 20  (2/5)    =    8

We have a prime factorization of $2^4 \times 3^3 \times 5^2 \times 7^2$

If we add one to each exponent, then add up all the exponents.

$5 + 4 + 3 + 3 = 15$

Therefore there are 15 natural factors.

Hope that helps!!!

🙃🙃👌

Let  x    = 4

x  >   sqrt (x)           1/x  =    1/4             1/sqrt (x)   =   1/sqrt (4)   =1/2

4  >  sqrt (4)

4 >   2

So....from least to greatest  we  have

1/x  , 1/sqrt (x)  , 1 , sqrt (x)   ,  x

2/11 are not bored....so..

The total number of people at the convention    =122  /(2/11)    =   671

Number  bored   =  671  ( 9    / 11  )    =   549

I'm  thinking  that  the last  sentence   should  be  "over  200 yards"

P(any drive  is > 200 yds)  =.40

P (any drive is < 200 yds)   =1  -.40    =  .60

P( 7  of 12  are over 200 yds)    =   C(12,7) *  ( .40)^7  * (.60)^5    ≈   10%

Possibilities

-5   -8       +               -8    7       -           7   4   +             4    -2     -

-5    7       -                 -8   4       -           7  -2   -

-5   4        -                -8  -2       +      

-5   -2      +

P( negative product)    = 6 / 10   =   3  /  5

Hello. You seem to be missing some information!

I got this question before, too. So I will assume that you have the same one:

Our club has 25 members, and wishes to pick a president, secretary, and treasurer. In how many ways can we choose the officers, if individual members are allowed to hold 2 but not all 3 offices?

Ummmm... the question is different in your link. So sorry, but it dosn't help.

Missing info.....

1994 to 2000 is 6 years        1.8% is .018 in decimal

3 381 000  *  ( 1+.018)⁶  =.............   people 

Call the roots   a , a + d   and  a  + 2d

Sum  of  the roots =  6

Sum of product of the  roots  taken two at a time  =  -13

So  we  have  this system

a + a + d  +  a  + 2d  =  6

a(a + d) +  a (a + 2d)  + (a + d) ( a + 2d)   =  -13

A little tedious to  solve this....so...I'm leaning on WolframAlpha  ( I can go through it if you  want me to)

We have  two possible  arithmetic  sequences

First one

a = -3   d  = 5

So

-3 , 2 , 7      are  the roots

So

( x + 3) ( x - 2) ( x - 7)    = x^3 - 6 x^2 - 13 x + 42  so k  =  -  42

Second one

a  = 7   d  =  -5

So   again

7 , 2 , -3     are  the roots and we  get  the same  value  for  k

And  the  median term    =  2

Oh I didn't think about using the conjugate. Thanks!

LCM    of  3 and  7    =  21

LCM  of  x^4   and  x   =  x^4

LCM  of y^2  and y^3   = y^3

LCM     of   3x^4y^2   and  7xy^3   =   21x^4y^3

If  3  - i   is a root....so is  3 + i

So  the polynomial  is of the  form

x^3  +  bx^2  + cx  +  d

b =  - sum of  the roots  =   =  -[ 2 + (3 + i)  + (3  - i)]  =  - 8

c =  sum of the product of  roots  taken two at a time  =    2(3 + i)  + 2 (3 -i)  + ( 3 + i) (3  -i)  =   6  + 6  + 9  - i^2  =  12  + 9 + 1   =   22

d  =  -  product of  the roots  = - 2 (3+i) ( 3 - i)   =  -  2 ( 9 -i*2)   = - 2 ( 9 + 1  )    =  -20

The polynomial  is

x^3     - 8x^2   +  22x   -  20

cos A  = sqrt  (5^2 - 3^2)   / 5  =  sqrt (16)   / 5   =  4/5

cos B =  sqrt  (13^2   -5^2)    /13   =   sqrt (144)  /  13  =  12  /  13

cos   ( A  - B)  = 

cos A cos B  +  sin A  sin B      filling in the  blanks, we  have

(4/5) ( 12/13)  +  ( 3/5) (5/13)   =

(48  + 15)  /  65   = 

63  /   65 

Here's  one way to do this  :

Let  P = (0,0)

Let Q  =  (3,0)

Connstruct  a circle centered at  P   with  a radius  of  2

The  equation is    x^2  + y ^2   = 4

Let the base of  PQR  =  PQ   = 3

So....the height of  PQR  can be found  as

2 = (1/2) 3  *  height

2  = 3/2  * height

height  = (2/3)(2)  =4/3

Sub  this into  the  equation of  the  circle   for  y

x^2 +  (4/3)^2  = 4

x^2  + 16/9  = 4

x^2   =  (36 - 16)  /9

x^2  =  20  / 9      take both roots

x = sqrt (20)/3   =   (2/3) sqrt (5)

x =  - sqrt(20)/3 = (-2/3)sqrt (5)

So  ....as  shown  in the  figure

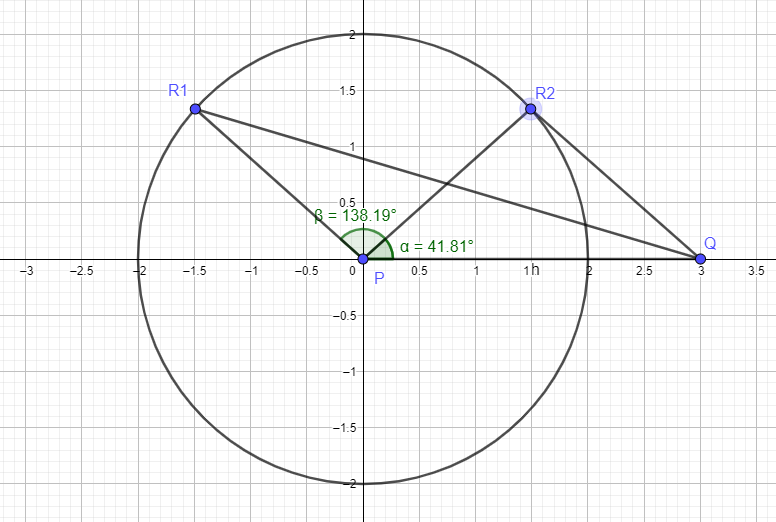
R1   =   ( -(2/3)sqrt 5  ,4/3)

R2  = ( (2/3)sqrt (5)  ,4/3)

Possible  angle  values of QPR  ≈  41.81°    and  ≈ 138.19°

\(\sum_{1}^{111} 2n = 12432\)              n = 111