Number 3
No. 3: Getting tougher still (as though that were possible)! Now it’s time for calculus. Guy D. Moore explains this one for us:
The problem asks us to ensure that three pieces form an acute triangle. Consider three pieces with lengths \(x>y>z\)
First, think about a right triangle. The formula for that, as our middle school teachers drilled into our heads, is \(x^2=y^2+z^2\). (Otherwise known as the Pythagorean Theorem.) To have an acute triangle, all angles must be less than 90 degrees, so we tweak that formula: \(x^2
From this we get that \(y and \((1-x)^2 , which is the same as
\(\begin{equation*}x<\frac{1-2y^2}{2(1-y)}\end{equation*} \)
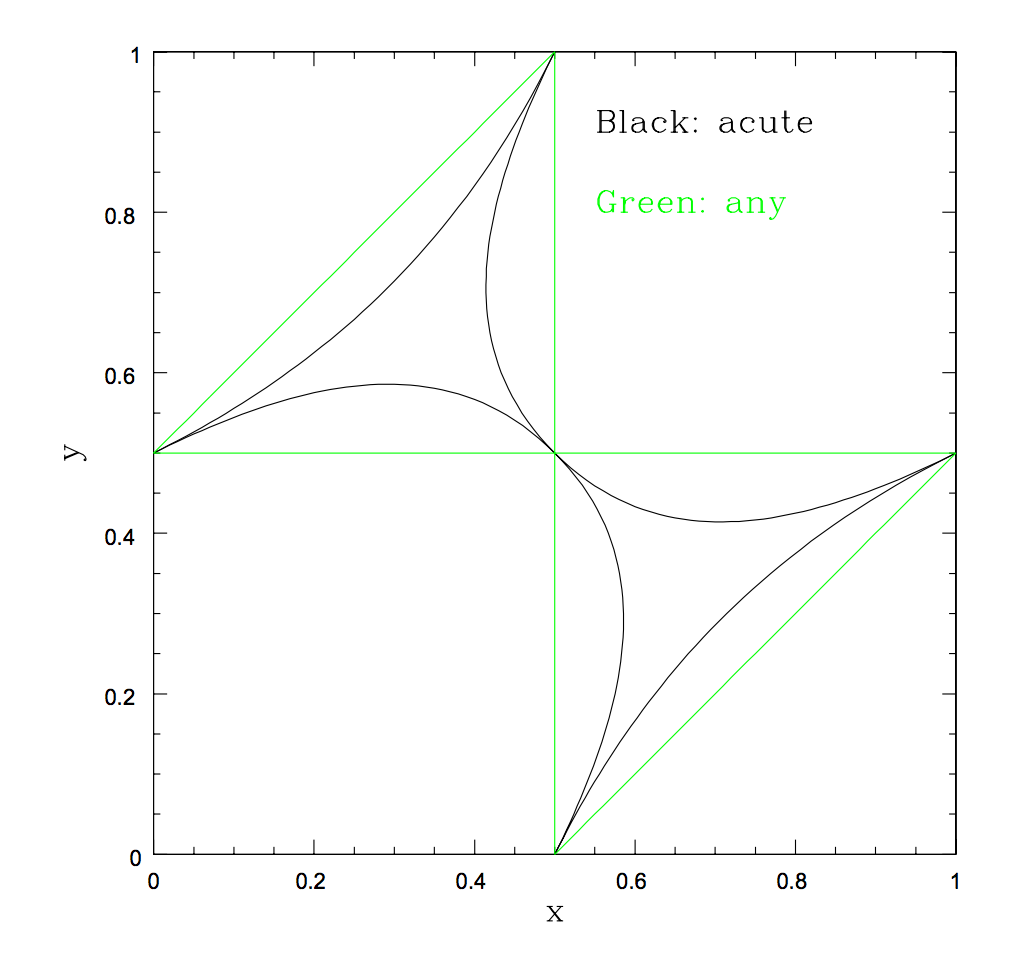
Since we’re dealing with pieces of the same stick and not three separate sticks, we can return to plotting in two dimensions, not three. And our mirrored-triangle plot is useful again since our answer lies within those two original triangles. This time, though, we need to draw two new three-pointed shapes within those two triangles. The area of those shapes will be our answer — the probability of an acute triangle.
So to calculate our new shapes, we need to cut pieces out of our original triangles. The area of one of those pieces is expressed in an integral (which is the calculus part of the solution). That integral is:
\(\begin{equation*}\int_0^{1/2}\frac{1-2y}{2-2y}dy=\frac{1-\ln(2)}{2}\end{equation*}\)
There are six shapes, each with the same area, cut out of our one-by-one square, leaving:
\(\begin{equation*}1-3(1-\ln(2))=\ln(8)-2\end{equation*}\)
In that equation, “ln” is the natural log, which equals an implied probability of acute triangle-formation of about 7.9 percent. (Who knew that natural logs are a great way to solve stick problems?) Guy also provided this illustration of the curvy areas we calculated: