All Answers 356741 Answers

CPhill: 9,900 km is "round trip." One-way trip should be=9,900/2=4,950 km.

Using the Law of Cosines we have

5^2  =  x^2  +  (x + 2)^2  - 2[ x (x +2)] cos (60)

25  = x^2 + x^2 + 4x + 4 - 2 [x^2 + 2x] (1/2)

25 = 2x^2  + 4x + 4 - x^2 - 2x

25 = x^2 + 2x + 4   rearrange as

x^2 + 2x  - 21  =  0

Using the quadratic formula, x  = √22 - 1  ≈ 3.69

(2,5) and (6,7)

Midpoint is  [  (2 + 6) / 2  , (7 + 5)/ 2 ]  = [ 8/2, 12/2 ] =  [4, 6 ]

And the perpendicular bisector  will pass through this point

And the perpendicular bisector  will have a negative reciprocal slope to the given line  = - 2/1 = -2

So......the equation of the perpendicular bisector is :

y =  -2 (x - 4) + 6

y  = -2x + 8 + 6

y = -2x + 14

Here's a graph : https://www.desmos.com/calculator/ehlzdpzpkp

Thanks so much!

a) Represent as a rational expression the time going to Germany.

The plane is being slowed by the wind so its rate is x - 50

The time going to Germany is  ....... Distance / Rate  =   9900 / [ x - 50]

b) Represent as a rational expression the time returning.

The plane is helped by the wind on the return trip....so its rate is  x + 50

And the time returning plus 4 hrs  = time going to Germany....so....we can represent (b) as

9900 / [ x + 50] + 4  =    [9900 + 4 [ x + 50] ]  / [ x + 50 ]

c) Write an equation representing the relationships between the times.

We have that

 9900 / [ x - 50] =    [9900 + 4 [ x + 50] ]  / [ x + 50 ]

d) What was the average rate of the plane in still air.

9900 / [ x - 50]  =  [  9900  + 4x + 200 ] / [ x + 50 ]       cross-multiply

9900 [ x + 50 ]  =  [ 10100 + 4x] [ x - 50]

9900x + 495000 =  10100x + 4x^2 - 505000 - 200x

9900x + 495000 =  9900x + 4x^2 - 505000      rearrange as

4x^2  - 1000000  =  0      divide through by 4

x^2   - 250000  = 0

x^2  =  250000            take the positive root of both sides

x =  500 km/ hr  =   speed in still air

e) How long did the round trip take?

Total time is   twice the return time plus 4 hours =   2 [  9900 / [ x + 50]   ]  + 4  = 

2 [ 9900 / 550 ] +  4  =

36   + 4  =     40  hrs

OMG after reading your solution i realised my result after first phrase should've been x^2 + 25x^2 - 110x -25 = 0 but i written -25x^2 for some reason  thx 

x^2 + y^2 =  25    ⇒ y^2  =  25 - x^2     (1)

5x - y = 11     ⇒  5x - 11  = y     (2)

Square  both sides of (2)  and we have that

(5x - 11)^2  = y^2

25x^2 - 110x + 121  = y^2          set this equal to (1)

25x^2 - 110x + 121  =  25 - x^2     add x^2 to both sides, subtract 25 from both sides

26x^2 -110x + 96 = 0      divide through by 2

13x^2 - 55x +  48  =  0      factor as

(13x  - 16) (x - 3)  = 0

Set both factors to 0, solve for x    and we have that  x = 16/13 and x  = 3

So using   5x - 11  = y 

5(16/13) - 11 =   80/13 - 11  =  [ 80 - 143] / 13 =  -63/13

5 (3) - 11 =  15 - 11  =  4

So.......the solutions are  (16/13, -63/13) and ( 3, 4)

thx that was correct.

oops i typed this wrong in the calculator 

2root 3^2 should be 12 

12- 3 = 9 

sqrt 9 = 3

PR is the hypotenuse of a right triangle  and PQ is a leg

So    √ [ PR^2 - PQ^2 ]  = QR  =  √  [ 8.2^2  - 1.8^2 ]  =  √ 64  = 8

So.........the perimeter of PQR  ≈    8.2 +  8  + 1.8  =  18 units 

sorry nice try that was incorrect.

Use pythagoras since it has a right angle ma boi

the formula for that is a^2 + b^2 + c^2

therefore 2sqrt(3)^2 - sqrt(3)^2 = (the missing side length)^2

2sqrt(3)^2 = 6 and sqrt(3)^2 =3 

6- 3 = 2 

bu then you have to sqrt your answer which means you have sqrt 2 at the end 

Let  x  = number of adults and y be the number of students

So  x + y  = 8    subtract x from both sides     ⇒      y = 8 - x   (1)

And number of adults * cost per ticket + number of students * cost per ticket  = total cost

So    x * 7.25  +  y * 5.50  = 52.75   (2)

Sub (1) into (2)   and we have

x * (7.25)  +  ( 8 - x) * 5.50  =  52.75     simplify

7.25x + 44 - 5.50x  =  52.75

1.75x + 44  =  52.75      subtract 44 from both sides

1.75 x  =  8.75    divide both sides by 1.75

x =  5 adult tickets

And since there were 8 total, the other 3 must be the number of children's tickets 

Thank you for answering this question however I was looking for a numerical value for a.

We can count sets, here

No. of sets possible  by choosing  any 2 numbers from 50  = C(50,2) = 1225

And we need to add to this 50 sets that have the same integer selected twice  = 50

And there are 16 integers that are multiples of 3  between 1 - 50

So.......the number of sets that don't contain a multiple of 3 is :

C (  50 - 16 , 2)  = C( 33 , 2) =   528  plus 33 additional sets of the same integer selected twice =

561

So......the probablity of selecting a set that contains one or two multiples of three is

1 -  [ 528 + 33 ] / [ 1225 + 50 ]  =  

1 - [ 561 ] / [1275 ]  =   

[1275 - 561 ] / 1275  =    14 / 25  =   56 / 100  =   56%    

54^54 =3 542 118 045 010 639 240 328 481 337 533 320 712 639 808 638 036 812 473 211 109 743 262 552 383 710 557 968 252 383 789 056.

59^59 =302 182 066 535 432 255 614 734 701 333 399 524 449 282 910 532 282 724 655 138 380 663 835 618 264 136 459 996 754 463 358 299 552 427 939.

We can count sets here.....

No. of possible sets  =  C(10,2)  = 45

No. of sets containing only letters from Cybil's name  = C(5,2)  = 10

No. of sets containing only letters from Ronda's name  = C(5,2)  = 10

So  the number of sets containing one letter from each name  =  45 - 10 - 10 = 25

So....the probability of choosing one of these sets  =  25 / 45  =  5 / 9  

I knew the answer for it so i wouldve told you it

Friday is mine too!

Thx Math Whiz.

1. Find the Slope

Finding the slope is relatively simple once you remember the formula. For me, I could not memorize any formulas unless I put them in words. I remember this formula as the ratio of the difference in y-values to x-values, if that helps. Anyway, here is the formula.

\(m=\frac{y_2-y_1}{x_2-x_1}\)

Now that the slope has been determined, one can move on to the next step.

2. Plug in a Coordinate for X and Y to Solve for B.

We now know the slope, so the equation of the line is now \(y=3x+b\). Based on the given info, we know that both Cartesian coordinates, (-3,-16) and (4,5) lie on this line. Substitute one point in its place for x and for y to findt he answer.

3. Write the Final Equation

Now that the only two necessary items, m and b, have been solved for, write the equation in y=mx+b format. 

m=3

b=-7

\(y=3x-7\)

You are done now!

 a+b=c, a+c=d, and b=c+d 

Rearrange as

c = b - d     (1)

c = d - a     (2)

c = a + b    (3)

Subtract (2)  from (1)

0 = (b - d) + (a - d)

d - a  = b - d

2d = a + b     So,  a + b  = c ⇒  c = 2d    and   b = 2d + d ⇒ b = 3d

So

a + 3d  = 2d

a = -d

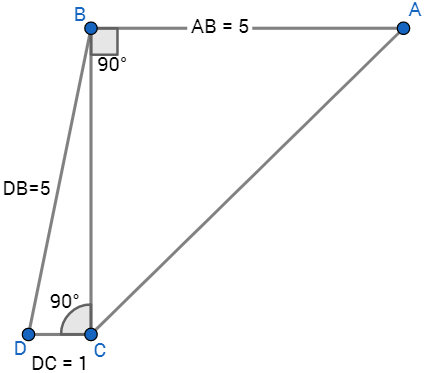
This image will make it easier to name individual segments, which should make the explanation more comprehensible. 

Using the Pythagorean's theorem, one can solve for BC.

Knowing this information, one can then solve for the missing side, AC in the diagram. 

Now that the hypotenuse of \(\triangle ABC\) has been solved for, you are done. 

Let A  =  (m, 13)      Let B  =  (n, 13)

Since the y coordinates are the same, the slope   = 0  and the y intercept  = 13

So...... the sum of the slope and y intercept is just 13