All Answers 356458 Answers

Thanks, so the second would be 52 right??

a. if the interest rate is 4% , the account will grow 4% more than the year before  EACH YEAR   

     initial 500 deposit will be worth   500 x 1.04 at the end of year 1 = $520

     at the end of the SECOND year, due to compounding, it will be worth   520 x 1.04=$ 540.80

   after 10 years    the formula becomes    500 (1.04)^10 = $ 740.12

b.1.04 is the interst applied PER YEAR     .... now the compounding period is 3 months....4 PERIODS per year..

..the periodic interest is then  .04/4 = .01/period    for 40 periods (10 years)

     and the formula becomes    

        500 (1.01)^40 = 744.43      NOTE: Due to COMPOUNDING this works out to be GREATER than 4% per year

                                                      (perhaps you have heard "APR"   = annual percentage rate     or

                                                              APY = annual percentage yield)

c. 1.04  = (1+x)^4      x = .009853  or 0..09853 %  per quarter compounding

d.  500 (1+ .009853)^40 = 740.12

1 - listfor(k, 3, 6, (2*k - 10)) =(-4, -2, 0, 2) = - 4

2 - listfor(k, 1, 4, (2*k^2 - 4)) = (-2, 4, 14, 28) = 44 

I'll do the first one.....see if you can do the second

1.   

First term  = 2(3) - 10  =  - 4

Last term = 2(6) - 10 = 12

Sum   = ( first term + last term) * (number of terms)  / 2   = (-4 + 12) (6 - 3 + 1) /2  =

(-4 + 12) (4) /2  =

8 ( 4) / 2 =

32 / 2  =

16

Second one

First term =  2(1)^2 - 4  =  -2

Last term = 2(4)^2 - 4  =  32 - 4  =  28

Number of terms  =  4

Thank you

Who    what   when     where     how     follow up      contact numbers      name    date  

The second answer

The article and the theme. Not being sarcastic btw.

First one 

-2.7, -8.3, -13.9 , -19.5, -25.1

The common difference is    -8.3 - (-2.7) = -5.6

The first term is  -2.7

So....the recursive rule is

a_n  = a_n-1 - 5.6   where a₁ = -2.7

Second one :

12.5, 11, 9.5.....

The common difference is    11 - 12.5  = -1.5

The first term is  12.5

So....the explicit rule is

a_n =  a₁ - 1.5(n - 1)   =  12.5  - 1.5n + 1.5   =  14 -1.5n

First term =  3(1)  = 3

Last term = 3(5) = 15

Sum = 

[  first term + last term ] *  number of terms / 2  =

[ 3 + 15  ] *  5 / 2  =

18 * 5  / 2  =

90 / 2   =

45

See the following image :

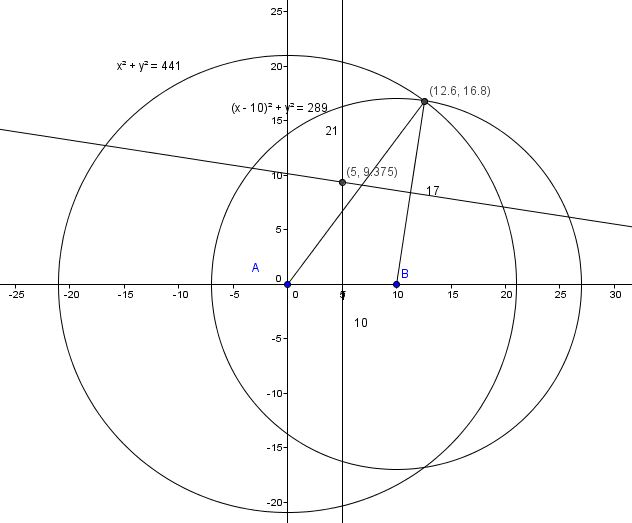
Let A = (0, 0)   B = (10, 0)

We can find C thusly

Construct a circle with a radius of 21 centered at  A

The equation of this circle  =  x^2 + y^2 = 441     (1)

Construct anothe circle with a radius of 17 centered at  B

The equation of the circle is  (x - 10)^2 + y^2 = 289     (2)

Subtract   (2) from (1)    and we get that

x^2 - (x - 10)^2 = 152  

x^2 - x^2 + 20x  - 100 = 152

20x - 252 = 0

20x = 252

x = 12.6  this is the x coordinate of C

And taking the positive  value for y

y =  sqrt (441 - (12.6)^2)  = 16.8

So....C = ( 12.6 , 16.8)

The midpoint of AC  = ( 6.3, 8.4)

The slope of the line between A and C is  8.4 /6.3 =  4/3

So...the equation of the perpendicular bisector to AC =

y = (-3/4) (x - 6.3) + 8.4      

And the midpoint of AB  = (5, 0)

So....the equation of the perpendicular bisector to AB = x = 5    

This is the x coordinate of the center of the circumscribing circle

The y value is      -.75 ( 5 - 6.3) + 8.4  = 9.375  = 9 + 3/8  =  75/8

So...the radius of the circumscribing circle is the distance from this point to A  ans is given by :

sqrt  (5^2 + (75/8)^2 )  =  sqrt  ( 1600 + 5625) / 8  =  sqrt (7225) / 8  =  85 / 8 

n = 2^3×3^2×5 = 360

360 =1, 2 | 3 | 4 | 5 | 6 | 8 | 9 | 10 | 12 | 15 | 18 | 20 | 24 | 30 | 36 | 40 | 45 | 60 | 72 | 90 | 120 | 180 | 360 (24 divisors)

Even divisors: 2, 4, 6, 8, 10, 12, 18, 20, 24, 30, 36, 40, 60, 72, 90, 120, 180, 360 =18

7! / 315 = 16

16 * 9 (Their GCD) = 144

LCM{315, 144} =7!

GCD{315, 144} =9

Thanks, Cphill!

I really struggle with these types of questions, so if you could help with these questions also that would be greatly appreciated!

1st one:

2nd one:

First one : cylinder

Second one : cone

Third one : pyramid

Last one : circle

1.   The common difference is   33......the first term is 20

So.....the formula is for the number sold in the nth week is

20 + 33 ( n - 1)  =

20 + 33n  - 33

33n  - 13

2.     a_n  =  -2n + 7

First term is   -2(1) + 7  =  5

Second term is   -2(2) + 7   =  3

So....the common difference is - 2

So....the recursive rule is   a_n  = a_n-1 - 2

So.....

a₁ = 5       a_n  = a_n-1 - 2

3.  2, 9, 16, 23 , 30

The common difference is  7

The first term is  2

So....the explicit formula for the nth term is

a_n =  2 + 7 ( n - 1)  =  2 + 7n - 7   =  -5 + 7n 

The first term is  -5

The common difference is 2

So...the 21st term =   -5 + 2 (21 - 1)  =  -5 + 2(20)  = 35

The sum, S,  of the series  =

( first term + last term ) ( number of terms) / 2  =

(-5 + 35) (21) /2  =

(30) * 21 / 2 =

(30/2) * 21  =

15 * 21 =

315

thanks

The roll of paper towels will form a "hollowed-out" cylinder.....

Call the radius of the hollow tube, r

Call the radius of the whole cylinder, R

The volume of the paper towels  = 

height of cylinder * pi  * (R^2 - r^2)

Maybe 62 ?

3a  

Vpyramid =   (1/3) (area of base) (height)   = (1/3) (15)^2 * 12  =  900 cm^3

3b

The scale  factor of the larger pyramid  = 3

The volume of the  actual pyramid  = (scale factor)^3  * ( volume of model)

So  ....volume of actual pyramid  =  (3)^3 * 900  = 24300 cm^3

3c....3b answers this.........3^3  =  27 times

thanks