2.
In cyclic quadrilaterla ABCD, AB=2, BC=3, CD=10, and DA=6.
Let P be the intersection of lines AB and CD.
Find the length BP.
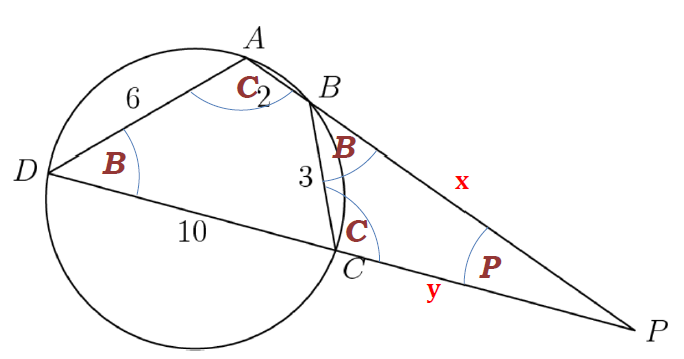
\(\text{Let $BP =x$} \\ \text{Let $PA =2+x$} \\ \text{Let $PC =y$} \\ \text{Let $PD =10+y$} \)
\(\text{Let $\angle BPC = P $} \\ \text{Let $\angle CBP = B $} \\ \text{Let $\angle ABC = 180^\circ -B $} \\ \text{Let $\angle ADC = 180^\circ - \angle ABC =180^\circ-(180^\circ -B)=B $} \)
1.
Intersecting secants theorem:
see: https://en.wikipedia.org/wiki/Intersecting_secants_theorem
\(\begin{array}{|rcll|} \hline \mathbf{BP\cdot PA} &\mathbf{=}& \mathbf{PC\cdot PD} \quad | \quad \text{Intersecting secants theorem} \\\\ x\cdot (2+x) &=& y\cdot (10+y) \\ \hline \end{array} \)
2.
sin-theorem:
\(\begin{array}{|lrcll|} \hline 1. & \dfrac{\sin(P)}{3} &=& \dfrac{\sin(B)}{y} \\ & \dfrac{\sin(P)}{\sin(B)} &=& \dfrac{3}{y} \\\\ 2. & \dfrac{\sin(P)}{6} &=& \dfrac{\sin(B)}{2+x} \\ & \dfrac{\sin(P)}{\sin(B)} &=& \dfrac{6}{2+x} \\ \hline & \dfrac{\sin(P)}{\sin(B)} = \dfrac{3}{y} &=& \dfrac{6}{2+x} \\\\ & \dfrac{3}{y} &=& \dfrac{6}{2+x} \\\\ & \dfrac{y}{3} &=& \dfrac{2+x}{6} \\\\ & y &=& \dfrac{3}{6}\cdot(2+x) \\\\ & \mathbf{y} & \mathbf{=}& \mathbf{\dfrac{1}{2}\cdot(2+x)} \\\\ & x\cdot (2+x) &=& y\cdot (10+y) \quad | \quad y = \dfrac{1}{2}\cdot(2+x) \\\\ & x\cdot (2+x) &=& \dfrac{1}{2}\cdot(2+x)\cdot \left(10+\dfrac{1}{2}\cdot(2+x)\right) \\\\ & x &=& \dfrac{1}{2} \cdot \left(10+ \dfrac{1}{2}\cdot(2+x) \right) \quad | \quad \cdot 2 \\\\ & 2x &=& 10+ \dfrac{1}{2}\cdot(2+x) \quad | \quad \cdot 2 \\\\ & 4x &=& 20+ 2+x \\\\ & 3x &=& 22 \\\\ & x &=& \dfrac{22}{3} \\\\ & \mathbf{ x } & \mathbf{=} & \mathbf{7.\bar{3}} \\ \hline \end{array}\)
![]()
Well now you have four answers, and you are too bloody dumb to know if any of them are correct.
Lets’ see ...
Rom’s answer agrees with CPhill’s, which he posted here: https://web2.0calc.com/questions/could-you-help-me-with-this-please-its-practicing (When you repeat questions, include the link to you previous posts.)
Rom’s answer is presented in pristine LaTex (not ASCII slop), which probably makes it consistent with your online text (or book), but you are not going to understand Rom’s answer any more than you understood CPhill’s answer. The reasons for this are appended to your previous post.
Keep in mind, if you are too lazy, or put-off, to go back to the prerequisites, you are not going to learn or understand this material. You just are wasting everyone’s time –including your own.![]()
GA
The reason you cannot teach yourself (this level of) math is because you lack the prerequisites.
To understand the solution to the question you posted, requires an understanding of the Binomial Cumulative Distribution Function. Your attempted answer did not include any binomial functions, and this indicates you are at least three prerequisites behind in the skills needed to solve problems of this type.
This video will help you understand the specific skills needed for your presented question.
For the prerequisites, start here: https://www.mathsisfun.com/data/index.html#stats
On this page are links for The Binomial Distribution.
Preceding those links is this one.
https://www.mathsisfun.com/combinatorics/combinations-permutations.html
You will need to understand this (and more) to understand the Binomial Cumulative Distribution Function.
GA