All Answers 358093 Answers

Quadrilateral PQRS is a square with a side length of \(13\).

Points \(X\) and \(Y\) lie outside the square so that \(PX=RY=12\) and \(QX=SY=5\).

Find \(\overline{XY}^2\).

\(\begin{array}{|rcll|} \hline \mathbf{\overline{XY}^2} &=& \mathbf{(13-2z)^2+(13+2h)^2} \quad &| \quad z=\sqrt{5^2-h^2} \\\\ &=& \left(13-2\sqrt{5^2-h^2}\right)^2+(13+2h)^2 \quad &| \quad h= \dfrac{5*12}{13} \\ &=& \left(13-2\sqrt{5^2-\dfrac{5^2*12^2}{13^2} }\right)^2 +\left(13+ \dfrac{10*12}{13}\right)^2 \\ &=& \left(13-2*5\sqrt{\dfrac{13^2-12^2}{13^2} }\right)^2 +\left(13+ \dfrac{120}{13}\right)^2 \\ &=& \left(13-2*5\sqrt{\dfrac{5^2}{13^2} }\right)^2 +\left(\dfrac{13^2+120}{13}\right)^2 \\ &=& \left(13-\dfrac{50}{13}\right)^2+\left(\dfrac{13^2+120}{13}\right)^2 \\ &=& \left( \dfrac{13^2-50}{13}\right)^2+\left(\dfrac{13^2+120}{13}\right)^2 \\ &=& \dfrac{ \left(13^2-50\right)^2+ \left(13^2+120\right)^2}{13^2} \\ &=& \dfrac{ 13^4-2*13^2*50+50^2+13^4+2*13^2*120+120^2}{13^2} \\ &=& \dfrac{ 13^2 \left( 2*13^2-100+240\right) } {13^2} +\dfrac{50^2+120^2}{13^2} \\ &=& 2*13^2-100+240 + 100 \\ &=& 2*13^2 +240 \\ &=& \mathbf{578} \\ \hline \end{array}\)

Find angle PRQ,

\(\text{Let $\angle PRQ = x $}\)

\(\begin{array}{|rcll|} \hline y+2*90^\circ + \theta &=& 360^\circ \\ y + \theta &=& 180^\circ \\ \mathbf{y} &=& \mathbf{180^\circ-\theta} \\\\ 120^\circ+130^\circ+y+x &=& 360^\circ \\ 250^\circ+y+x &=& 360^\circ \\ y+x &=& 110^\circ \quad | \quad \mathbf{y=180^\circ-\theta} \\ 180^\circ-\theta+x &=& 110^\circ \\ -\theta+x &=& -70^\circ \\ \mathbf{\theta} &=& \mathbf{70^\circ +x} \\\\ x &=& \dfrac{\theta}{2} \quad | \quad \mathbf{\theta=70^\circ +x} \\\\ x &=& \dfrac{70^\circ +x}{2} \\\\ 2x &=& 70^\circ + x \\ \mathbf{ x} &=& \mathbf{70^\circ} \\ \hline \end{array}\)

I have drawn it to scale and have the answer 10 degrees but i cannot see why.

Thanks Geno, that is a excellent method. 

It always pays to do a quick sketch and then facts like this are more likely to be seen.

Here is the super long methods.

I'd  have let the centre of the circle be (x,y)

Then found the distances and said they had  to be equal.

\(r^2=(x-6)^2+(y-2)^2\qquad(1)\\ r^2=(x-8)^2+(y-6)^2\qquad (2)\\ r^2=(x-8)^2+(y-10)^2 \qquad (3)\\~\\ (3)-(2)\\ 0=(y-6)^2-(y-10)^2\\ 0=y^2-12y+36-(y^2-20y+100)\\ 0=y^2-12y+36-y^2+20y-100\\ 0=8y-64\\ 0=y-8\\ y=8\\~\\ sub\;\; in\\ r^2=(x-6)^2+(6)^2\qquad(1b)\\ r^2=(x-8)^2+(2)^2\qquad (2b)\\ subtract\\ 0=(x-6)^2+36-(x-8)^2-4\\ 0=(x^2-12x+36)+36-(x^2-16x+64)-4\\ 0=-12x+36+36+16x-64-4\\ 0=4x+4\\ x=-1 \)

\(r^2=(x-2)^2+(y-6)^2\qquad(1)\\ r^2=(x-8)^2+(y-6)^2\qquad (2)\\ r^2=(x-8)^2+(y-10)^2 \qquad (3)\\~\\ (3)-(2)\\ 0=(y-6)^2-(y-10)^2\\ 0=y^2-12y+36-(y^2-20y+100)\\ 0=y^2-12y+36-y^2+20y-100\\ 0=8y-64\\ 0=y-8\\ y=8\\~\\ sub\;\; in\\ r^2=(x-2)^2+(0)^2\qquad(1b)\\ r^2=(x-8)^2+(0)^2\qquad (2b)\\ subtract\\ 0=(x-2)^2-(x-8)^2\\ 0=(x^2-4x+4)-(x^2-16x+64)\\ 0=-4x+4+16x-64\\ 0=12x-60\\ x=5\\~\\ \text{So the centre is (5,8)} \)

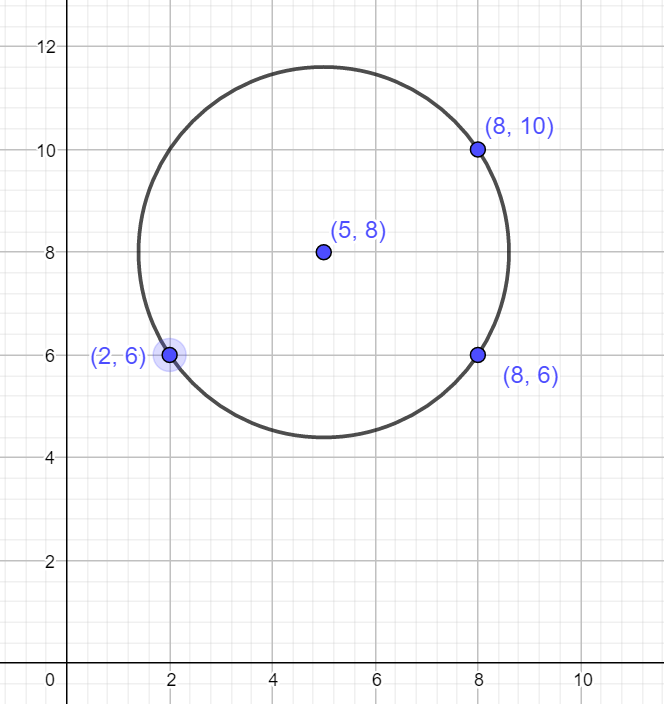
Coding:

r^2=(x-2)^2+(y-6)^2\qquad(1)\\
r^2=(x-8)^2+(y-6)^2\qquad (2)\\
r^2=(x-8)^2+(y-10)^2 \qquad (3)\\~\\

(3)-(2)\\
0=(y-6)^2-(y-10)^2\\
0=y^2-12y+36-(y^2-20y+100)\\
0=y^2-12y+36-y^2+20y-100\\
0=8y-64\\
0=y-8\\
y=8\\~\\
sub\;\; in\\
r^2=(x-2)^2+(0)^2\qquad(1b)\\
r^2=(x-8)^2+(0)^2\qquad (2b)\\
subtract\\
0=(x-2)^2-(x-8)^2\\
0=(x^2-4x+4)-(x^2-16x+64)\\
0=-4x+4+16x-64\\
0=12x-60\\
x=5\\~\\
\text{So the centre is (5,8)}
 

Here is your pic, drawn to scale

the radius of the bigest circle is 7

the radius of the second biggest circle is 5

the radius of the little circles is 1

Now you can work out all the areas that are needed and find the fraction requested.

Here is the question

I'll try numbrrer 5;    this one's a bit tricky

  Important: In a proportion "Total" is always 100%  and  "Part" can be any number, including 100 and larger             

 Question:    15 is what percent of 5 ?

 Part  =   15

 Total =    5  (100%)

  Percent  = ?              5 : 100%  =  15 : X      X = (100% * 15) / 5    X = 300% 

  Answer:   15 is 300% of 5.        

We can dissect ABCDEF into several triangles.  Answer: 27 sqrt(2)

The answer is 7.79.

The answer is 3/8.

Start by getting a common denominator then I will help more.

I believe that the answer is b.

iv won't be correct if there is a constant in the remainder.

LInk: https://www.chegg.com/homework-help/questions-and-answers/figure-shows-five-shaded-circles-within-circle-radius-7-units-four-small-congruent-shaded--q23591399

hit x hit x miss  =  .80 x .80 x .20  =  .128

hit x miss x hit  =  .80 x .20 x .80  =  .128

miss x hit x hit  =  .20 x .80 x .80  =  .128

Adding these together:                     .384

This cannot be answered without the picture.

Here is the link : https://latex.artofproblemsolving.com/2/e/c/2ec388968eb94bbd38898fefa6dcdf9224e84ebf.png

D=5; C=3; 5 nCr 3 * 5^(5 - 3) / 6^5 =3.21502057 % 

The answer is (c) 

WHAT is the shaded portion? 

Let # drinks = x

  then  10 -x  is # sandwiches

$ 3 * x   +  $ 5 * (10-x)    = $ 42       solve for 'x' which is the number of drinks ....then #  sandwiches = 10 - x

                      x²     -x    +8

       _____________________________________

x+3 |   x^3 + 2x^2 + 5x +12

           x^3 + 3x^2

          __________________________

                  -x^2 + 5x + 12

                  -x^2 -3x  

              ________________________

                            8x  +12

                            8x  +24

                    ______________________ 

                                    -12

Red is quotient     green is remainder......

12 + 16 + 20 + 24 + 28 + 32 + 36 + 40 =    ??  

You will need 3 6's and 2 not-6's.

The probability of getting a 6 is 1/6; the probability of getting a not-6 is 5/6.

(1/6)(1/6)(1/6)(5/6)(5/6)  =  25/7776.

You will need to multiply this answer by the number of ways that 3 6's can be chosen:  ₅C₃ = 10.

Answer =  10 x 25 / 7776  =  0.0322  or  125/3888.

Since angle(YOW) = 100^o, arc(YZW) = 100^o.

Since angle(ZYW) = 10^o, arc(ZW) = 20^o.

Subtracting, arc(YZ) = 80^o.

Angle(YWZ) = ½Arc(YZ) = 40^o.