One focus of the ellipse \(\dfrac{x^2}{2} + y^2 = 1 \)is at \(F = (1,0)\)
There exists a point \(P = (p,0)\), where p > 0 such that for any chord \(\overline{AB}\) that passes through \(F\)
angles \(\angle APF\) and \(\angle BPF\) are equal.
Find \(p\).
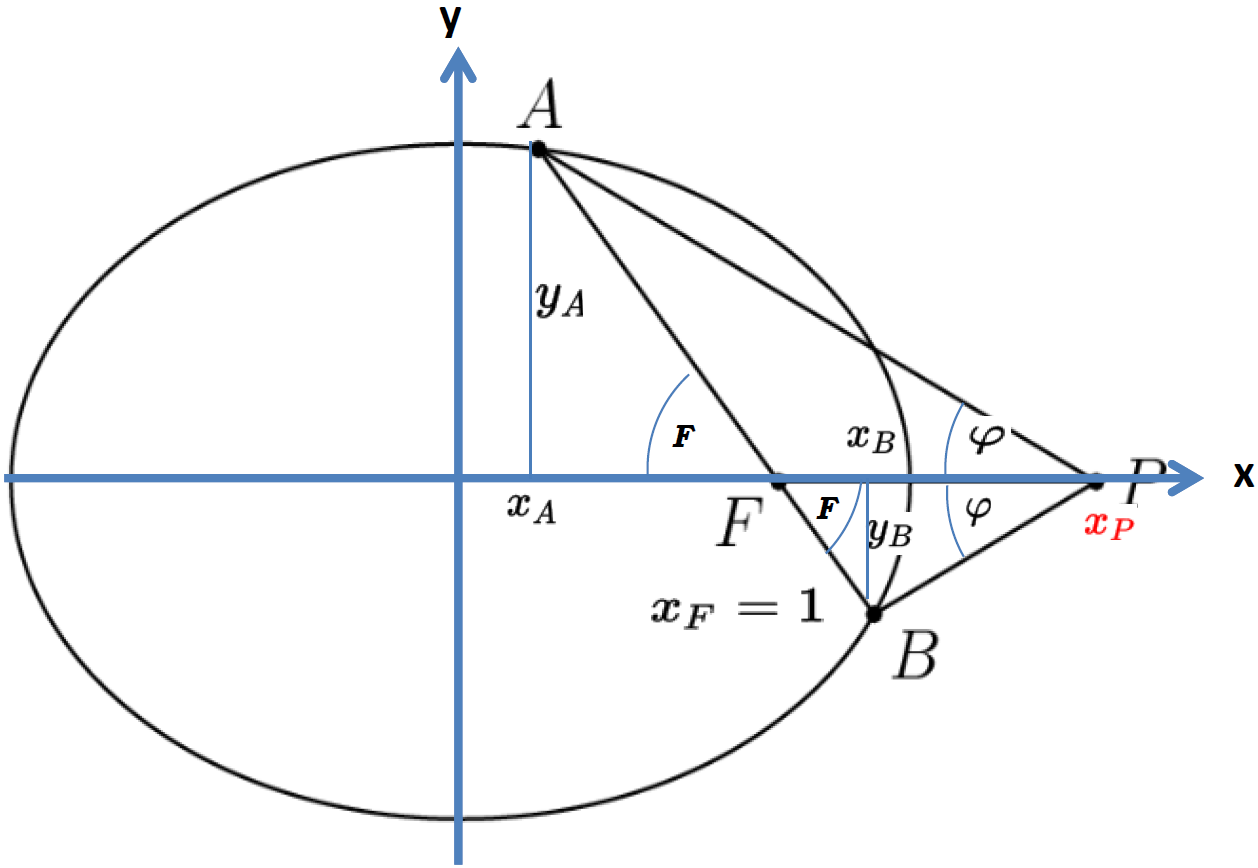
\(\text{Let $ \angle APF = \angle BPF = \varphi$ }\)
\(\begin{array}{|rcll|} \hline \tan{\varphi} = \dfrac{y_A}{x_P-x_A} &=& \dfrac{-y_B}{x_P-x_B} \\\\ \dfrac{y_A}{x_P-x_A} &=& \dfrac{-y_B}{x_P-x_B} \\\\ \mathbf{\dfrac{y_A}{y_B}} &=&\mathbf{ -\dfrac{(x_P-x_A)}{(x_P-x_B)}} \\ \hline \\ \tan{F} = \dfrac{y_A}{x_F-x_A} &=& \dfrac{-y_B}{x_B-x_F} \\\\ \dfrac{y_A}{x_F-x_A} &=& \dfrac{-y_B}{x_B-x_F} \\\\ \dfrac{y_A}{y_B} &=& -\dfrac{(x_F-x_A)}{(x_B-x_F)} \quad | \quad x_F = 1 \\ \\ \mathbf{\dfrac{y_A}{y_B}} &=&\mathbf{ -\dfrac{(1-x_A)}{(x_B-1)}} \\ \hline \dfrac{y_A}{y_B} = -\dfrac{(x_P-x_A)}{(x_P-x_B)} &=& -\dfrac{(1-x_A)}{(x_B-1)} \\\\ -\dfrac{(x_P-x_A)}{(x_P-x_B)} &=& -\dfrac{(1-x_A)}{(x_B-1)} \\\\ \dfrac{x_P-x_A}{x_P-x_B} &=& \dfrac{1-x_A}{x_B-1} \\\\ (x_B-1)(x_P-x_A) &=& (1-x_A)(x_P-x_B) \\ \cdots \\ \mathbf{x_P} &=& \mathbf{ \dfrac{2x_Ax_B-(x_A+x_B)} {x_A+x_B-2} } \\ \hline \end{array}\)
line \(y=mx+b\):
\(\begin{array}{|rcll|} \hline y &=& mx+b \quad | \quad F = (1,0) \text{ is on the line } \\ y_F &=& mx_F +b \quad | \quad y_F =0 \quad x_F = 1 \\ 0 &=& m*1 +b \\ b &=& -m \\\\ y &=& mx+b \quad | \quad b = -m \\ y &=& mx-m \\ y &=& m(x-1) \quad | \quad \text{equation of the line through F } \\ \mathbf{y^2} &=& \mathbf{m^2(x-1)^2} \\ \hline \end{array}\)
ellipse \(\dfrac{x^2}{2} + y^2 = 1\):
\(\begin{array}{|rcll|} \hline \dfrac{x^2}{2} + y^2 &=& 1 \\ \mathbf{ y^2} &=& \mathbf{1-\dfrac{x^2}{2}} \\ \hline \end{array}\)
intersection line - ellipse:
\(\begin{array}{|rcll|} \hline y^2 = m^2(x-1)^2 &=& 1-\dfrac{x^2}{2} \\\\ m^2(x-1)^2 &=& 1-\dfrac{x^2}{2} \\\\ m^2(x^2-2x+1) &=& 1-\dfrac{x^2}{2} \\\\ m^2 x^2-2m^2x+m^2 &=& 1-\dfrac{x^2}{2} \\\\ m^2 x^2-2m^2x+m^2 -1+\dfrac{x^2}{2} &=& 0 \\\\ x^2\left(m^2+\dfrac{1}{2}\right)-2m^2x+ (m^2 -1) &=& 0 \\\\ x &=& \dfrac{2m^2\pm \sqrt{4m^4 - 4 \left(m^2+\dfrac{1}{2}\right)(m^2 -1)} }{2\left(m^2+\dfrac{1}{2}\right)} \\\\ x &=& \dfrac{2m^2\pm 2\sqrt{m^4 - \left(m^2+\dfrac{1}{2}\right)(m^2 -1)} }{\left(2m^2+\dfrac{1}{2}\right)} \\\\ x &=& \dfrac{m^2\pm \sqrt{m^4 - \left(m^2+\dfrac{1}{2}\right)(m^2 -1)} }{\left(m^2+\dfrac{1}{2}\right)} \\\\ x &=& \dfrac{m^2\pm \sqrt{ \dfrac{1+m^2}{2} } }{\left(m^2+\dfrac{1}{2}\right)} \\\\ \mathbf{ x_A} &=& \mathbf{\dfrac{m^2+ \sqrt{ \dfrac{1+m^2}{2} } }{\left(m^2+\dfrac{1}{2}\right)}} \\\\ \mathbf{ x_B} &=& \mathbf{\dfrac{m^2- \sqrt{ \dfrac{1+m^2}{2} } }{\left(m^2+\dfrac{1}{2}\right)} }\\ \hline \end{array}\)
\(\mathbf{x_A =\ ?}\quad \mathbf{x_B =\ ?}\)
For example we set \(m = 1 \text{$(~$for any chord $\overline{AB}$ that passes through $F$ angles $\angle APF$ and $\angle BPF$ are equal$~)$}\)
\(\begin{array}{|rcll|} \hline x_A &=& \dfrac{1^2+ \sqrt{ \dfrac{1+1^2}{2} } }{\left(1^2+\dfrac{1}{2}\right)} \\\\ x_A &=& \dfrac{1+ \sqrt{ \dfrac{2}{2} } }{\left(1+\dfrac{1}{2}\right)} \\\\ x_A &=& \dfrac{1+ 1}{\left(1+\dfrac{1}{2}\right)} \\\\ x_A &=& \dfrac{2}{ \dfrac{3}{2} } \\\\ \mathbf{x_A} &=& \mathbf{\dfrac{4}{3}} \\ \hline \\ x_B &=& \dfrac{1^2- \sqrt{ \dfrac{1+1^2}{2} } }{\left(1^2+\dfrac{1}{2}\right)} \\\\ x_B &=& \dfrac{1- \sqrt{ \dfrac{2}{2} } }{\left(1^2+\dfrac{1}{2}\right)} \\\\ x_B &=& \dfrac{1- 1}{\left(1^2+\dfrac{1}{2}\right)} \\\\ x_B &=& \dfrac{0}{\left(1^2+\dfrac{1}{2}\right)} \\\\ \mathbf{x_B} &=& \mathbf{0} \\ \hline \end{array}\)
\(\mathbf{x_P =\ ?}\)
\(\begin{array}{|rcll|} \hline \mathbf{x_P} &=& \mathbf{ \dfrac{2x_Ax_B-(x_A+x_B)} {x_A+x_B-2} } \\\\ x_P &=& \dfrac{2*\dfrac{4}{3}*0-\left(\dfrac{4}{3}+0\right)} {\dfrac{4}{3}+0-2} \\\\ x_P &=& \dfrac{ -\dfrac{4}{3}} {\dfrac{4}{3}-2} \\\\ x_P &=& \dfrac{ -\dfrac{4}{3}} {\dfrac{4-6}{3}} \\\\ x_P &=& \dfrac{ -4} {-2} \\\\ \mathbf{ x_P} &=& \mathbf{2} \\ \hline \end{array}\)
\(P = (p,~0)\\ p=x_P=2 \\ P = (2,~0)\)
In general:
\(\begin{array}{|rcll|} \hline x^2\left(m^2+\dfrac{1}{2}\right)-2m^2x+ (m^2 -1) &=& 0 \quad | \quad :\left(m^2+\dfrac{1}{2}\right) \\\\ x^2-\dfrac{2m^2}{\left(m^2+\dfrac{1}{2}\right)}x+ \dfrac{(m^2 -1)}{\left(m^2+\dfrac{1}{2}\right)} &=& 0 \\\\ x^2\underbrace{-\dfrac{2m^2}{\left(m^2+\dfrac{1}{2}\right)}}_{=-(x_A+x_B)}x+ \underbrace{\dfrac{(m^2 -1)}{\left(m^2+\dfrac{1}{2}\right)}}_{=x_A*x_B} &=& 0 \\ \boxed{\text{Vieta's formulas:}\\ \text{The roots } r_1 ,\ r_2\text{ of the quadratic polynomial } \\ P(x)=a x^2 + b x + c \text{ satisfy}\\ r_1 + r_2 = -\dfrac{b}{a},\ r_1 r_2 = \dfrac{c}{a}. } \\ \hline \mathbf{x_A+x_B} &=& \mathbf{\dfrac{2m^2}{\left(m^2+\dfrac{1}{2}\right)}} \\\\ \mathbf{x_A*x_B} &=& \mathbf{\dfrac{(m^2 -1)}{\left(m^2+\dfrac{1}{2}\right)}} \\ \hline \end{array}\)
\(\begin{array}{|rcll|} \hline \mathbf{x_P} &=& \mathbf{ \dfrac{2x_Ax_B-(x_A+x_B)} {x_A+x_B-2} } \\\\ && \mathbf{x_A+x_B} = \mathbf{\dfrac{2m^2}{\left(m^2+\dfrac{1}{2}\right)}} \\\\ && \mathbf{x_A*x_B} = \mathbf{\dfrac{(m^2 -1)}{\left(m^2+\dfrac{1}{2}\right)}} \\\\ x_P &=& \dfrac{2\dfrac{(m^2 -1)}{\left(m^2+\dfrac{1}{2}\right) } -\dfrac{2m^2}{\left(m^2+\dfrac{1}{2}\right)}} {\dfrac{2m^2}{\left(m^2+\dfrac{1}{2}\right)}-2} \\\\ x_P &=& \dfrac{\dfrac{2(m^2 -1)-2m^2}{\left(m^2+\dfrac{1}{2}\right) } } {\dfrac{2m^2}{\left(m^2+\dfrac{1}{2}\right)} -2\dfrac{\left(m^2+\dfrac{1}{2}\right)}{\left(m^2+\dfrac{1}{2}\right)}} \\\\ x_P &=& \dfrac{\dfrac{2(m^2 -1)-2m^2}{\left(m^2+\dfrac{1}{2}\right) } } {\dfrac{2m^2-2\left(m^2+\dfrac{1}{2}\right)}{\left(m^2+\dfrac{1}{2}\right)} } \\\\ x_P &=& \dfrac{2(m^2 -1)-2m^2} {2m^2-2\left(m^2+\dfrac{1}{2}\right) } \\\\ x_P &=& \dfrac{2m^2 -2-2m^2}{2m^2-2m^2-1} \\\\ x_P &=& \dfrac{-2}{-1} \\\\ \mathbf{x_P} &=& \mathbf{2} \quad (p=2) \\ \hline \end{array}\)
