All Answers 355939 Answers

It is really good to thank people but do not assume that all answers are correct.

465(x-25) = 315(x+25)

        150x = 19500

              x = 130

I get the following:

If the speed of the wind is 25 mph, then the plane's speed against the wind must be 415 mph, NOT 315 mph !!

[465  +  415] / 2 =440 mph - its speed in still air.

[465  -  415] / 2 =25 mph - the speed of the wind.

Determine the value of \(2002 + \frac{1}{2} \left( 2001 + \frac{1}{2} \left( 2000 + \dots + \frac{1}{2} \left( 3 + \frac{1}{2} \cdot 2 \right) \right) \dotsb \right)\).

\(\begin{array}{|rcll|} \hline s&=& 2002 + \frac{1}{2} \left( 2001 + \frac{1}{2} \left( 2000 + \dots + \frac{1}{2} \left( 3 + \frac{1}{2} \cdot 2 \right) \right) \dotsb \right) \\ s &=& 2002 + 2001\left(\frac{1}{2}\right) + 2000 \left(\frac{1}{2}\right)^2+ \dots +3\left(\frac{1}{2}\right)^{1999} + 2 \left(\frac{1}{2}\right)^{2000} \\ && \boxed{ \text{We substitute }x =\frac{1}{2} } \\ s &=& 2002 + 2001x + 2000x^2+ \dots +3x^{1999} + 2x^{2000} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline s &=& 2002 + & 2001x + 2000x^2+ \dots +3x^{1999} + 2x^{2000} \\ xs &=& & 2002x + 2001x^2 + \dots +4x^{1999} + 3x^{2000} + 2x^{2001} \\ \hline xs-s &=& &x + x^2 + \dots +x^{1999}+ x^{2000}+ 2x^{2001}-2002 \\ s(x-1) &=& & x\underbrace{(1+ x^2 + \dots +x^{1999})}_{\mathbf{= \frac{1-x^{2000}}{1-x}} }+ 2x^{2001}-2002 \\ s(x-1) &=& & \frac{ x(1- x^{2000})} { 1-x}+ 2x^{2001}-2002 \quad | \quad x =\frac{1}{2} \\\\ s(\frac{1}{2}-1) &=& & \frac{ \frac{1}{2} \left(1-\left(\frac{1}{2}\right)^{2000} \right)} {1-\frac{1}{2}}+ 2\left(\frac{1}{2}\right)^{2001}-2002 \\ -\frac{1}{2}s &=& & 1-\left(\frac{1}{2}\right)^{2000} + 2\left(\frac{1}{2}\right)^{2001}-2002 \\ -\frac{1}{2}s &=& & 1-\left(\frac{1}{2}\right)^{2000} + 2\left(\frac{1}{2}\right)^{2000}\frac{1}{2}-2002 \\ -\frac{1}{2}s &=& & 1-\left(\frac{1}{2}\right)^{2000} + \left(\frac{1}{2}\right)^{2000} -2002 \\ -\frac{1}{2}s &=& & 1 -2002 \\ \frac{1}{2}s &=& & 2002-1 \\ \frac{1}{2}s &=& & 2001 \\ \mathbf{s} &=& & \mathbf{4002} \\ \hline \end{array}\)

\(2002 + \frac{1}{2} \left( 2001 + \frac{1}{2} \left( 2000 + \dots + \frac{1}{2} \left( 3 + \frac{1}{2} \cdot 2 \right) \right) \dotsb \right) = \mathbf{4002}\)

5000=150 * [((1 + 0.03/12)^N - 1) / (0.03/12)], solve for N
5000 = 60000. (1.0025^N - 1)
1/12 = 1.0025^N - 1
13/12= 1.0025^N
Take the log of both sides
N = log(13/12)/log(1.0025) =32.057 months

Lorraine and Dolores are in an event where they have to carry the same weight of items in order to advance to the next stage. Lorraine is carrying 5250g worth of items. Dolores is carrying 5/21 the weight that Lorraine is carrying. How much worth of items must Lorraine give to Dolores in order for them to have items of the same weight? (Leave your answer in grams)

In triangle \(XYZ\), we have \(\angle X = 60^\circ\) and \(\angle Y = 45^\circ\).
The bisector of \(\angle X\) intersects \(\overline{YZ}\) at point D, and \(DX = 24\).
What is the area of triangle \(XYZ\)?

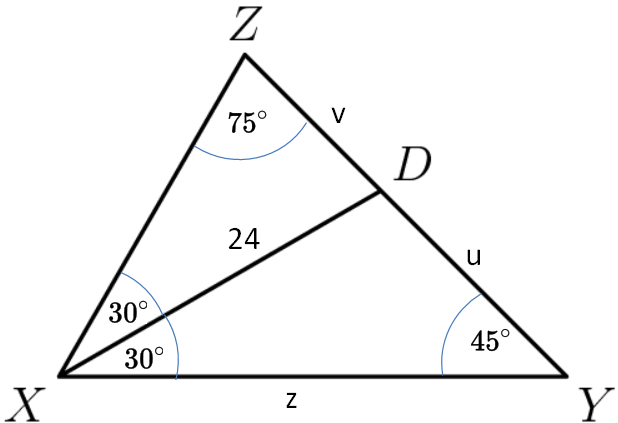
sin-rule:

\(\begin{array}{|rcll|} \hline \dfrac{\sin(30^\circ)}{u} &=& \dfrac{\sin(45^\circ)}{24} \\\\ \mathbf{u} &=& \mathbf{\dfrac{24 \sin(30^\circ)}{\sin(45^\circ)}} \\ \hline \end{array} \begin{array}{|rcll|} \hline \dfrac{\sin(30^\circ)}{v} &=& \dfrac{\sin(75^\circ)}{24} \\\\ \mathbf{v} &=& \mathbf{\dfrac{24 \sin(30^\circ)}{\sin(75^\circ)}} \\ \hline \end{array}\)

\(\mathbf{u+v = \ ?}\)

\(\begin{array}{|rcll|} \hline u+v &=& \dfrac{24 \sin(30^\circ)}{\sin(45^\circ)} + \dfrac{24 \sin(30^\circ)}{\sin(75^\circ)} \\\\ u+v &=& 24 \sin(30^\circ) \left( \dfrac{1}{\sin(45^\circ)} + \dfrac{1}{\sin(75^\circ)} \right) \\ && \boxed{\sin(45^\circ) = \dfrac{\sqrt{2}}{2} \\ \sin(75^\circ) = \dfrac{1+\sqrt{3}} {2\sqrt{2}} \\ \sin(30^\circ) = \dfrac{1}{2} } \\ u+v &=& \dfrac{24}{2} \left( \dfrac{2} {\sqrt{2}} + \dfrac{2\sqrt{2}}{1+\sqrt{3}} \right) \\ u+v &=& 24 \left( \dfrac{1} {\sqrt{2}} + \dfrac{ \sqrt{2}}{1+\sqrt{3}} \right) \\ \ldots \\ \mathbf{u+v} &=& \mathbf{12\sqrt{6}} \\ \mathbf{\left(u+v\right)^2} &=& \mathbf{864} \\ \hline \end{array}\)

sin-rule:

\(\begin{array}{|rcll|} \hline \dfrac{\sin(60^\circ)}{u+v} &=& \dfrac{\sin(75^\circ)}{z} \\\\ \mathbf{z} &=& \mathbf{\dfrac{(u+v) \sin(75^\circ)}{\sin(60^\circ)}} \\ \hline \end{array}\)

The area of triangle \(XYZ\):

\(\begin{array}{|rcll|} \hline A &=& \dfrac{z(u+v)\sin(45^\circ)}{2} \quad | \quad \mathbf{z=\dfrac{(u+v) \sin(75^\circ)}{\sin(60^\circ)}} \\\\ A &=& \dfrac{ \left(u+v\right)^2\sin(45^\circ)\sin(75^\circ)}{2\sin(60^\circ)} \quad | \quad \mathbf{\left(u+v\right)^2=864} \\\\ A &=& \dfrac{864\sin(45^\circ)\sin(75^\circ)}{2\sin(60^\circ)} \\\\ A &=& \dfrac{432\sin(45^\circ)\sin(75^\circ)}{\sin(60^\circ)} \\\\ && \boxed{\sin(45^\circ) = \dfrac{\sqrt{2}}{2} \\ \sin(75^\circ) = \dfrac{1+\sqrt{3}} {2\sqrt{2}} \\ \sin(60^\circ) = \dfrac{\sqrt{3}}{2} } \\ A &=& \dfrac{432\sqrt{2}}{2} \dfrac{(1+\sqrt{3})} {2\sqrt{2}} \dfrac{2}{\sqrt{3}} \\\\ A &=& 216 \dfrac{(1+\sqrt{3})} {\sqrt{3}} \\\\ A &=& 216 \dfrac{(1+\sqrt{3})} {\sqrt{3}} \dfrac{\sqrt{3}}{\sqrt{3}} \\\\ A &=& \dfrac{216}{3} (1+\sqrt{3})\sqrt{3} \\\\ A &=& 72(1+\sqrt{3})\sqrt{3} \\\\ A &=& 72(3+\sqrt{3}) \\ \mathbf{A} &=& \mathbf{340.707658145 } \\ \hline \end{array}\)

The two equations are:

-3 - 4t = -4 + 8s    (1)       and   0 + t = k - 2s    (2)

Rearrange these as follows:

from (1):   t = 1/4 - 2s

from (2):   t = k - 2s

So k = 1/4

Hmm!  MathCad gives the following result:

The length of a rectangle is 3 more than its width. The perimeter of the rectangle is 58 cm. What are the rectangle’s dimensions?

( 58 - 2*3) / 4 = 13            Rectanle sides are:  a = 13cm   b = 16cm  

Keith buys 3 kiwis and 4 zucchini's for a total of $4.95. A Kiwi costs $0.25 more than a zucchini. What is the cost of 1 kiwi and 1 zucchini?

(4.95 - 3*0.25) / 7 = 0.6           Zucchini costs 60 cents  and  kiwi costs 85 cents.

                                              Therefore, the cost of  1 kiwi and 1 zucchini is $ 1.45  

I'm getting different result; triangle area  A ≈ 340.71 u²  

Triangles  XMD and XND are identical.

CPhill: Did you forget the formula for the "sum of consecutive squares"??

n = 1000; a = 1/6 * (2*n + 1)*n*(n + 1) =333,833,500

angle XWZ = Angle WYX

Thus triangle WXZ similiar to triangle WXY. We get:

XZ/8 = 8/14

XZ=32/7

Hence: YZ=14-32/7=66/7

First, we need to find out how many silver cars needed to be added for the ratio 1:3. We can scale it up, making 1:3 to 40:120. After that, then you just need to find out how many you have to add. We can do 120-20, which means you have to add 100 silver cars. 

100 SILVER CARS.

Thank you very much!

Thank you!

Thanks!

Thanks!

Thank you!

Thanks!

(4H+2M)-(3H-1M)=1H AND 1M (SUBTRACT LIKE TERMS)

SUBTRACT PRICES: $13.50-$9.25=$4.25

1 HAMBURGER AND 1 MILKSHAKE IS $4.25.