All Answers 355970 Answers

Last one

a)  Making the same assumption as in the estimated mean in the  last problem  we have

[  2(7.5)  + 9(12.5)  + 5(17.5)  + 5 (22.5)  + 3(27.5) ]  /  [ 2 + 9 + 5 + 5 + 3]  ≈  17  min

b) Fraction finishing  in less than 20 min   =   [ 5 + 9 + 2 ]   / [ 2 + 9 + 5 + 5 + 3 ]  =  16 / 24  = 2/3  

Second one 

a) class interval that contains the median

We have  30  values

The  median  occurs  between the 15th and 16th value

The interval where this occurs  is     2 ≤ h < 3

b)  mean .....I'm less sure about this one because we don't actually know how many hours any particular individual spends on his/her tablet

But let's assume that each individual spends the midpoint of their class interval as a representative time on their tablet

[ For instance....assume that  every one in the first class interval spends   1/2  hr on their phone.....everyone in the second class interval spens 1 + 1/2  hrs on their phone, etc.]

So......one estimate  of the mean is

[ 4 (1/2)  +  8 (1 + 1/2)  + 11(2 + 1/2)  + 7(3 + 1/2) ]   / 30   ≈   2.2 hrs

First one

Mean height of team  =

[ (1)(198)  + (3)(199)  + (2)(200) + (5)(201)  + (2)(202) ]  / [ 1 + 3 + 2 + 5 + 2 ]  =

[2604/ 13]  =

200.3 cm

Let x  be the  height of the new player.....and we  have

[ 2604 + x ] / 14   = 201    multiply both sides by 14

2604 + x   =  2814        subtract 2604 from both sides

x  = 210  cm

Thanks, alan......that's a very crafty solution   !!!!!

Rewrite the equation as:   b = 3(a + 2)/(a + 5)

Let z = a+5    z is also an integer

Then  b = 3(z-3)/z  or   b = 3 - 9/z

For this to result in an integer, we must have 9/z as an integer.  This means the following values are the only ones allowed for z:

z = -9, -3, -1, 1, 3, 9  which means  a = -14, -8, -6, -4, -2, 4  with corresponding values for b of:  b = 4, 6, 12, -6, 0, 2

I'll leave you to order them in pairs.

\(\displaystyle\int e^{csc (π+t)} * csc (π+t) cot (π+t)\; dt\\ =\displaystyle\int e^{-csc (t)} *-csc (t) cot (t)\; dt\\ =-\displaystyle\int e^{-csc (t)} *csc (t) cot (t)\; dt\\~\\ \qquad \;\;\;Let\;\;u=-csc(t)\\ \qquad \qquad \;\;u=-(sin(t))^{-1}\\ \qquad \qquad \;\;\frac{du}{dt}=(sin(t))^{-2}*cos(t)\\ \qquad \qquad \;\;\frac{du}{dt}=\frac{cos(t)}{(sin(t))^2}\\ \qquad \qquad \;\;\frac{du}{dt}=csc(t)cot(t)\\~\\ \qquad \qquad \;\;dt=\frac{du}{csc(t)cot(t)}\\~\\ =-\displaystyle\int e^{-csc (t)} *csc (t) cot (t)\; dt\\~\\ =-\displaystyle\int e^{u} *csc (t) cot (t)\; \frac{du}{csc(t)cot(t)}\\~\\ =-\displaystyle\int e^{u} du\\~\\ =-e^u+c\\ =-e^{-csc(t)}+c\)

LaTex:

\displaystyle\int e^{csc (π+t)} * csc (π+t) cot (π+t)\; dt\\
=\displaystyle\int e^{-csc (t)} *-csc (t)  cot (t)\; dt\\
=-\displaystyle\int e^{-csc (t)} *csc (t)  cot (t)\; dt\\~\\
\qquad \;\;\;Let\;\;u=-csc(t)\\
\qquad \qquad \;\;u=-(sin(t))^{-1}\\
\qquad \qquad \;\;\frac{du}{dt}=(sin(t))^{-2}*cos(t)\\
\qquad \qquad \;\;\frac{du}{dt}=\frac{cos(t)}{(sin(t))^2}\\
\qquad \qquad \;\;\frac{du}{dt}=csc(t)cot(t)\\~\\
\qquad \qquad \;\;dt=\frac{du}{csc(t)cot(t)}\\~\\

=-\displaystyle\int e^{-csc (t)} *csc (t)  cot (t)\; dt\\~\\
=-\displaystyle\int e^{u} *csc (t)  cot (t)\; \frac{du}{csc(t)cot(t)}\\~\\
=-\displaystyle\int e^{u} du\\~\\
=-e^u+c\\
=-e^{-csc(t)}+c

You could do it graphically as follows:

Alternatively, you could do it algebraically by letting the epicenter have coordinates (x, y) and then using Pythagoras to express the distance between (x, y) and any two of the given points to find x and y (you only need two of the points because you only need to find two unknowns).

Compute
\(\dfrac{1^2}{2^1} + \dfrac{2^2}{2^2} + \dfrac{3^2}{2^3} +~ \ldots~ + \dfrac{n^2}{2^n} +~ \ldots\)

\(\small{ \begin{array}{|rcllll|} \hline \text{Sum}&=& \mathbf{\dfrac{1^2}{2^1}} &\mathbf{+\dfrac{2^2}{2^2}} &\mathbf{+ \dfrac{3^2}{2^3}} &\mathbf{+ \dfrac{4^2}{2^4}} &\mathbf{+~ \ldots~ + \dfrac{n^2}{2^n} +~ \ldots } \\\\ &=& 1^2\left(\dfrac{1}{2}\right) &+2^2\left(\dfrac{1}{2}\right)^2 &+3^2\left(\dfrac{1}{2}\right)^3 &+4^2\left(\dfrac{1}{2}\right)^4 &+~ \ldots~ + n^2\left(\dfrac{1}{2}\right)^n \quad | \quad r = \dfrac{1}{2} \\\\ &=& 1^2r&+2^2r^2&+3^2r^3&+4^2r^4 &+~ \ldots~ + n^2r^n +~ \ldots~ \\\\ &=& 1r &+4r^2 &+9r^3 &+16r^4 &+~ \ldots~ \\\\ &=& 1r &+1r^2 &+1r^3 &+1r^4 &+~ \ldots~ \quad | \quad s_1=r(1+r+r^2+r^3+~ \ldots~ ) \\ & & &+3r^2 &+3r^3 &+3r^4 &+~ \ldots~ \quad | \quad s_2=3r^2(1+r+r^2+r^3+~ \ldots~ ) \\ & & & &+5r^3 &+5r^4 &+~ \ldots~ \quad | \quad s_3=5r^3(1+r+r^2+r^3+~ \ldots~ ) \\ & & & & &+7r^4 &+~ \ldots~ \quad | \quad s_4=7r^4(1+r+r^2+r^3+~ \ldots~ ) \\ & & & & &\ldots & +~ \ldots~ \quad | \quad \ldots \\ \hline \end{array} \\ \begin{array}{|rcllll|} \hline &=& \left(s_1+s_2+s_3+s_4+~ \ldots~\right) \\ &=& \left(r+3r^2+5r^3+7r^4+~ \ldots~\right) \left(1+r+r^2+r^3+~ \ldots~ \right) \quad | \quad 1+r+r^2+r^3+~ \ldots = \dfrac{1}{1-r} \\ &=& \dfrac{1}{1-r}\left(r+3r^2+5r^3+7r^4+~ \ldots~\right) \\ \mathbf{\text{Sum}} &=& \mathbf{\dfrac{1}{1-r}S } \quad | \quad S= r+3r^2+5r^3+7r^4+~ \ldots \\ \hline \end{array} }\)

\(\small{ \begin{array}{|rcllll|} \hline \mathbf{S}&=& \mathbf{r} &\mathbf{+3r^2} &\mathbf{+5r^3} &\mathbf{+7r^4} &+~ \ldots \\ &=& r &+r^2 &+r^3 &+r^4 &+~ \ldots \quad | \quad S_1=r(1+r+r^2+r^3+~ \ldots~ ) \\ & & &+2r^2 &+2r^3 &+2r^4 &+~ \ldots \quad | \quad S_2=2r^2(1+r+r^2+r^3+~ \ldots~ ) \\ & & & &+2r^3 &+2r^4 &+~ \ldots \quad | \quad S_3=2r^3(1+r+r^2+r^3+~ \ldots~ ) \\ & & & & &+2r^4 &+~ \ldots \quad | \quad S_4=2r^4(1+r+r^2+r^3+~ \ldots~ ) \\ & & & & &\ldots& +~ \ldots~ \quad | \quad \ldots \\ \hline \end{array} \\ \begin{array}{|rcllll|} \hline &=& \left(S_1+S_2+S_3+S_4+~ \ldots~\right) \\ &=& \left(r+2r^2+2r^3+2r^4+~ \ldots~\right) \left(1+r+r^2+r^3+~ \ldots~ \right) \quad | \quad 1+r+r^2+r^3+~ \ldots = \dfrac{1}{1-r} \\ &=& \dfrac{1}{1-r}\left(r+2r^2+2r^3+2r^4+~ \ldots~\right) \\ &=& \dfrac{r}{1-r}\left(1+2r+2r^2+2r^3+~ \ldots~\right) \\ &=& \dfrac{r}{1-r}\left(1+2r(1+r+r^2+r^3~ \ldots~)\right) \quad | \quad 1+r+r^2+r^3+~ \ldots = \dfrac{1}{1-r} \\ &=& \dfrac{r}{1-r}\left(1+2r\left(\dfrac{1}{1-r}\right)\right) \\ &=& \dfrac{r}{1-r}\left(1+\dfrac{2r}{1-r}\right) \\ \mathbf{S}&=& \mathbf{\dfrac{r}{1-r}\left(\dfrac{1+r}{1-r}\right)} \\ \hline \end{array} }\)

\(\begin{array}{|rcll|} \hline \mathbf{\text{Sum}} &=& \mathbf{\left(\dfrac{1}{1-r}\right)S } \quad | \quad \mathbf{S=\dfrac{r}{1-r}\left(\dfrac{1+r}{1-r}\right)} \\\\ \text{Sum}&=&\left(\dfrac{1}{1-r}\right)\left(\dfrac{r}{1-r}\right)\left(\dfrac{1+r}{1-r}\right) \\\\ \text{Sum}&=&\dfrac{r(1+r)}{(1-r)^3} \quad | \quad r=\dfrac{1}{2} \\\\ \text{Sum}&=&\dfrac{\dfrac{1}{2}\left(1+\dfrac{1}{2}\right)}{\left(1-\dfrac{1}{2}\right)^3} \\\\ \text{Sum}&=&\dfrac{\dfrac{1}{2}\left(\dfrac{3}{2}\right)}{\left(\dfrac{1}{2}\right)^3} \\\\ \text{Sum}&=&\dfrac{\left(\dfrac{3}{2}\right)}{\left(\dfrac{1}{2}\right)^2} \\\\ \text{Sum}&=&\dfrac{\left(\dfrac{3}{2}\right)}{\left(\dfrac{1}{4}\right)} \\\\ \text{Sum}&=&\dfrac{12}{2} \\\\ \mathbf{\text{Sum}}&=& \mathbf{6} \\ \hline \end{array}\)

2.5PX = 5y(h)/24    (1)

3.5PY = 7y(h)/24    (2)

Multiply both sides of (1) by 24/5

2.5PX*24/5 = y(h)     (3)

Use (3) to replace y(h) in (2)

3.5PY = (7/24)*(2.5PX*24/5)

3.5PY = 7/5PX

PX = 3.5*(5/7)*PY

PX = (7/2)*(5/7)*PY

PX = 5/2PY  or PX = 2.5PY

Thanks LuckyDuck,

Choy, if you want to repost please give the address of your original question and ask people to answer there. 

Hi Littlemixfan,

Find the number of pairs of integers (x,y) with x is less than 0, y is less than 10, that satisfy

\(\frac{1}{1-\frac{10}{x}} > 1 - \frac{5}{y}\)

First I want to look at formula restrictions.   

\(y\ne0\\ x\ne0\\ x\ne10\)

We also have the question restriction of

\(x<0\qquad and \qquad y<10\)

So where can it be so far:

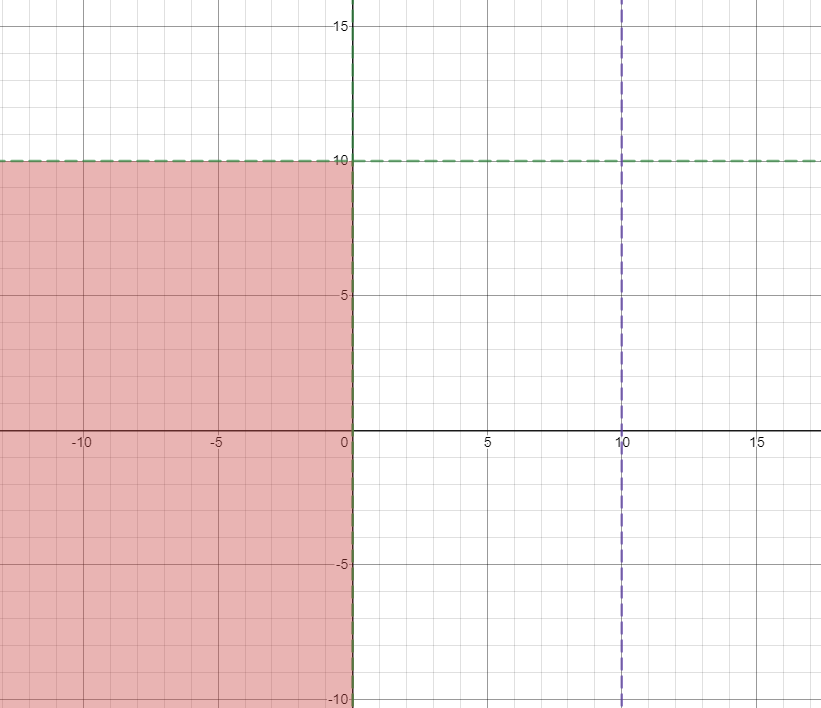
NOW

\(\frac{1}{1-\frac{10}{x}} > 1 - \frac{5}{y}\\ \frac{1}{\frac{x-10}{x}} > 1 - \frac{5}{y}\\ \frac{x}{x-10} > \frac{x-10}{x-10} - \frac{5}{y}\\ \frac{x-(x-10)}{x-10} > - \frac{5}{y}\\ \frac{10}{x-10} > - \frac{5}{y}\\ \frac{x-10} {10}< - \frac{y}{5}\\ - \frac{y}{5}>\frac{x-10} {10} \\ \frac{y}{5}<\frac{-x+10} {10} \\ \frac{y}{1}<\frac{-x+10} {2} \\ y<-0.5x+5 \)

So that is underneath the line y=-0.5x+5

NOTE: Maybe I made an error but I do not think so. Maybe it was meant to be a   <   sign.

Also,:

I left the > sign in for all my working but it would have been easier just to solve for = and then test the regions afterwards.

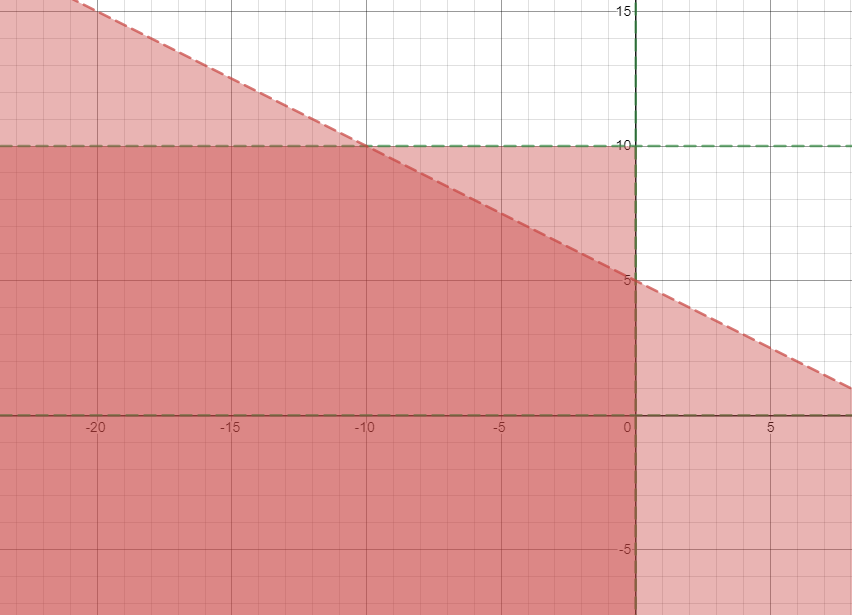
So far I have these 2 regions.  But since there are 2 regions one where y<0 and one where y>0 I will test both.

Test  (-1,+1) and (-1,-1)

\(\frac{1}{1-\frac{10}{x}} > 1 - \frac{5}{y}\\test\;(-1,1)\\ \frac{1}{11}>-4\quad true \\ test\;(-1,-1)\\ \frac{1}{11}>6\quad false \\ \)

So here is the region:

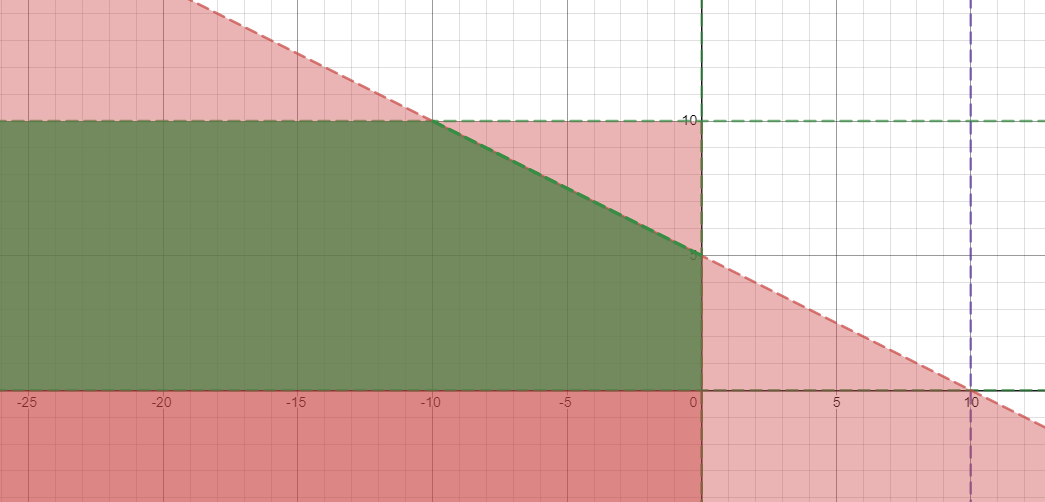
I think there is an infinite number of integer pair solutions.

LaTex:

\frac{1}{1-\frac{10}{x}} > 1 - \frac{5}{y}\\
\frac{1}{\frac{x-10}{x}} > 1 - \frac{5}{y}\\
\frac{x}{x-10} > \frac{x-10}{x-10} - \frac{5}{y}\\
\frac{x-(x-10)}{x-10} >  - \frac{5}{y}\\
\frac{10}{x-10} >  - \frac{5}{y}\\
\frac{x-10} {10}<  - \frac{y}{5}\\
- \frac{y}{5}>\frac{x-10} {10} \\

\frac{y}{5}<\frac{-x+10} {10} \\

\frac{y}{1}<\frac{-x+10} {2} \\

y<-0.5x+5

Geometry - Analytic Geometry

Of Course!

Thanks!

............... ................ ...........

Lol 

The calculator said this...  

log49

Is this the same question?

https://web2.0calc.com/questions/perhaps-the-most-common-error-in-ranking-poker-hands-involves-confusing-the-order-of-a-straight-and-a-flush-a-straight-is-5-cards-with-cons

Well, correct me if I'm wrong, but a+2=b, and a+5=3.  We can change the equation, to make it _+5=3, then we can revere it so it says 3-5=_, or rather a.  That equation simplified would be a=(-2).  Now that we know a=(-2), we can see that b=0.  I'm not sure if this is what you're looking for, but I hope that this helps! 

sqrt (3*3^2)  -  sqrt(4*3) + sqrt (3*100)

3 sqrt 3        - 2 sqrt 3     +  10 sqrt 3

(3-2+10)(sqrt 3)

11 sqrt 3

A city that has an elevation of 15 meters is closer to sea level than a city that has an elevation of-10 meters. 

I disagree.  15 meters above sea level is 5 meters farther from the top of the water than –10 meters below. 

Exaggerate the conditions to make it obvious.  What if you said

A city that has an elevation of 5000 meters is closer to sea level than a city that has an elevation of –10 meters. 

This technique is similar to the "reductio ad absurdum" form of argument. 

_.

Well... OK I disagree

oh, no problem! ill just wait and ask other people. thanks you your help though! 

I'm very sorry I haven't learned this...

I asked some people do but they are eating dinner of AFK

I'm dumb I don't understand anything