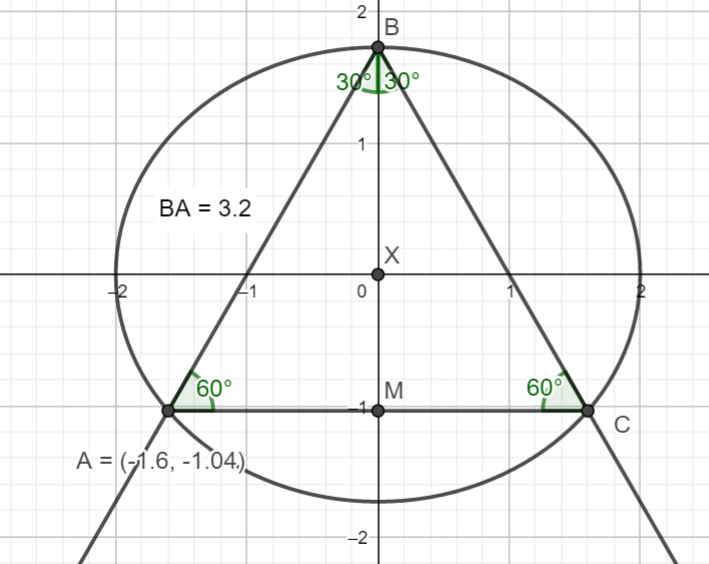
Since it is a ratio question you can use a convenient ellipse.
Let X be the centre and M be the midpoint of AC
triangle BXF2 and triangle BMA are similar tiranges and they are both 30, 60 90 degree triangles.
So their sides are in the ration 1:2:sqrt3
I want the focal length (c) to be 1 and
I want B to be \((0,\sqrt3)\)
\(c^2=a^2-b^2\\ 1=a^2-3\\ 4=a^2\\ a=2\)
So the ellipse that I will use is
\(\frac{x^2}{4}+\frac{y^2}{3}=1\\ \frac{y^2}{3}=1-\frac{x^2}{4}\)
Equation of line AB
\(y=\sqrt3\;x+\sqrt3\\ y=\sqrt3(x+1)\\ y^2=3(x+1)^2\\ \frac{y^2}{3}=(x+1)^2\\ \)
Solve simultaneously
\(1-\frac{x^2}{4}=(x+1)^2\\ -\frac{x^2}{4}=x^2+2x\\ -x^2=4x^2+8x\\ 5x^2+8x=0\\ x(5x+8)=0\\ x=0\quad or \quad x=-\frac{8}{5} \)
So the x value for A is -8/3
\(AC=AB=BC=\frac{16}{5}\\ F_2F_1=2\\ \frac{AB}{F_1F_2}=\frac{16}{10}=\frac{8}{5} \)