All Answers 358108 Answers

I assume a_1, a_2, a_3, ... is an arithmetic sequence, because there are no a_5 in the problem.

For an arithmetic sequence a_n, \(a_{n - k} + a_{n + k} = 2a_n\). So \(a_1 + a_5 = 2a_3\) by plugging in n = 3, k = 2.

Therefore, 

\(3a_3 = -12\\ a_3 = -4\)

Now you just solve \(\begin{cases}a_1 + a_5 = -8\\a_1a_5 = -30\end{cases}\) to find the values of a_1 and a_5. That way, you will know the possible common differences of the arithmetic sequence. Then you can use \(a_{10} = a_1 + 9(\text{common difference})\) to calculate the possible values of a_{10}. 

Neither 2u nor 2u doesn't make much sense to me. Please check if that is a typo.

Anyways, if u is a number such that 2u is not in the interval (-1, 1), that means \(2u \leq -1\text{ or }2u \geq 1\). Solving each inequality gives \(u \leq -\dfrac12 \text{ or }u \geq \dfrac12\). Then the answer is \(\left(-\infty, -\dfrac12\right] \cup \left[\dfrac12, \infty\right)\)

Moving the 6cm edge outwards to align with the 3cm edge and moving the edge marked with b outwards to align with the 7cm edge gives a rectangle with dimensions 10cm x 9cm, and the sides are unchanged, so the perimeter is unchanged.

Now you can calculate the perimeter of the original figure by calculating the perimeter of the rectangle, which is much easier compared to the original problem. 

I hope this helps.

For the first one, you can look at the terms pairwise:

\((1 - 2) + (3 - 4) + (5 - 6) + \cdots + (2019 - 2020) + 2021\)

Each pair results in -1 and there are 1010 pairs of numbers (that is just 2020/2), so the answer is \((-1)(1010) + 2021 = 1011\).

Some numbers are missing from your second question. Please check again.

For the third question, look at the terms pairwise again:

\(\quad(1 + 4) +(2 + 8) + (3 + 12) + (4 + 16) + \cdots + (24 + 96) + (25 + 100) \\ =5 + 10 + 15 + 20 + \cdots + 120 + 125\)

Now that is just the sum of an arithmetic sequence. You can find the first term, common difference, and the number of terms, then plug it into the formula to calculate it.

If you want to walk from Mytown to Capital City, you go like this (assuming there are no shortcuts):

Mytown -> Little Village -> Capital City

or this:

Mytown -> Yourtown -> Capital City

The first path is (8 + 51) miles long and the second path is (6 + 37) miles long. Whichever one is shorter is the distance required.

The axis is just another word for the diameter. Therefore the diameter is 14 units, meaning the radius is 7 units.

Now you can use the formula \(\text{surface area} = 4\pi (\text{radius})^2\) to finish it off.

So, let \(h \times w \times l\) be the dimensions of that prism.

We have \(\begin{cases}2(hw + wl + hl) = 56\\h + w + l = 56\end{cases}\). We are to find \(\sqrt{h^2 + w^2 + l^2}\).

We can use the identity \((h + w + l)^2 = (h^2 + w^2 + l^2) + 2(hw + wl + hl)\) to calculate \(h^2 + w^2 + l^2\), and then take square root. I will leave that as an exercise for you.

If you don't believe the identity is true, try to expand the left hand side and the right hand side. \((h + w + l)^2 = ((h + w) + l)^2 = (h + w)^2 + 2l(h + w) + l^2\) and etc.

Triangle inequality implies \(\begin{cases} 3 + 6 > AC\\ 3 + AC > 6\\ 6 + AC > 3\\ 9 + AC > 12\\ 9 + 12 > AC\\ 12 + AC > 9 \end{cases}\). If you list the integers satisfying all 6 inequalities, the possible values would be 4, 5, 6, 7, 8.

Let w be the length of the top side of the top-left rectangle. Then the left side of the top-left rectangle is \(\dfrac 3w\) and the left side of the bottom-left rectangle is \(\dfrac 7w\). This suggests the heights of the rectangle are in the ratio 3 : 7.

Since the top side of the top-right rectangle and that of the bottom-right rectangle are the same, the area ratio of the top-right rectangle and that of the bottom-right rectangle is also 3 : 7, which means \(x = 12 \times \dfrac 73 = 28\).

We use Euclidean algorithm to simplify \(\gcd(3n + 4, 7n + 15)\).

\(\quad \gcd(3n + 4, 7n + 15)\\ = \gcd(3n+4, n + 7)\\ = \gcd(-17, n + 7)\\ = \gcd(n + 7, 17)\)

If x is an integer, \(\gcd(x, 17)\) can only be either 1 or 17. That means the sum of all possible values required is 1 + 17 = 18.

Let a, b, c, d, e, x be the 6 numbers, with x being the number that is removed.

\(\begin{cases}\dfrac{a + b + c + d + e + x}6 = 14\\\dfrac{a + b +c + d + e}5 = 10\end{cases}\)

That means a + b + c + d + e = 50. Substitute that into the first equation to get \(\dfrac{50 + x}6 = 14\).

Can you work out the value of x from here? That is the number that was removed.

Note that the exterior angles of any convex polygon always add up to 360 degrees.

Since an interior angle and its corresponding exterior angle always add up to 180 degrees, a larger exterior angle means a smaller interior angle. So we are actually looking for the largest exterior angle.

Using the ratio, we calculate that the largest exterior angle is \(360^\circ \times \dfrac{7}{3 + 5 + 7} = 168^\circ\). You can subtract that from 180 degrees to find the smallest interior angle. 

This is one step away from the answer. Please continue on your own, but I hope you have an idea of what I explained, because that would be useful if you are to solve a similar problem entirely on your own.

Let a and b be the two numbers.

\(\begin{cases}a^2 + b^2 = 327\\ab = 85\end{cases}\)

We want to find a + b, but we only have quadratic terms in our equations, so we consider (a + b)^2 instead.

\((a + b)^2 = a^2 +b^2 + 2ab = 327 + 2(85) = 497\)

Suppose x = a + b. Then x^2 = 497. Can you take it from here?

Hint: The value of x is NOT negative since a and b are nonnegative numbers.

Let x be the original number.

Then 5x/(7 + x) = 8. Multiplying by (7 + x) on both sides gives 5x = 8x + 56. You can move the terms around to find the value of x.

This is equivalent to finding the number of solutions to the nine linear Diophantine equations \(a_1 + a_2 + a_3 + \cdots + a_{10} = 10, 20, 30, \cdots, 90\), You can do that using stars-and-bars method, but it will be very tough.

So, this is the diagram of the question: 

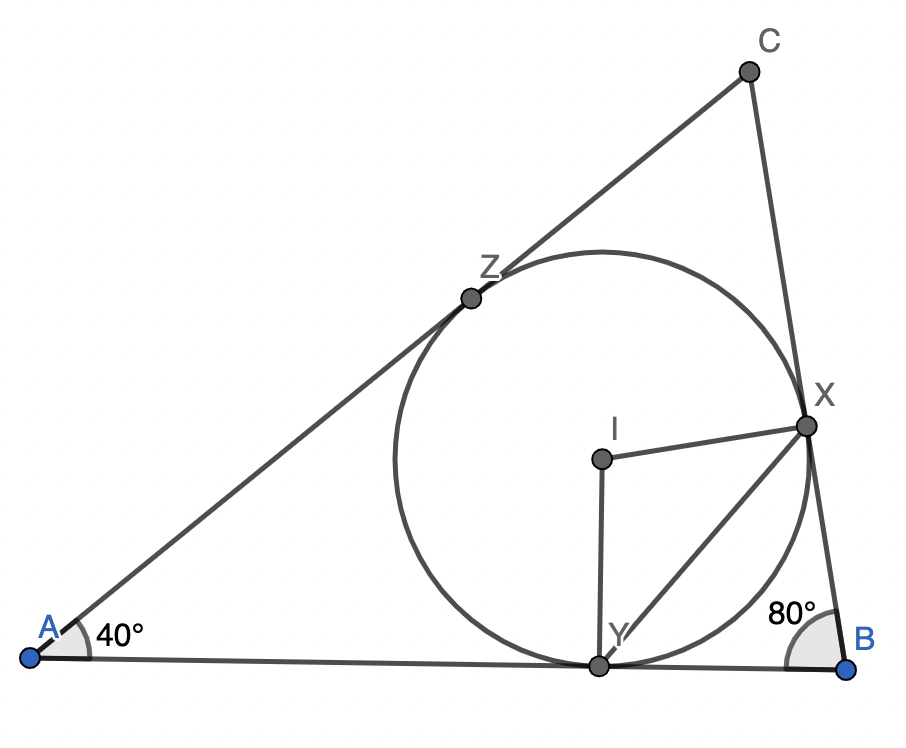
The point I is the center of the incircle, i.e., the incenter of triangle ABC.

By tangent properties, we have \(\angle IYB = \angle IXB = 90^\circ\).

Since \(\angle IYB + \angle IXB = 180^\circ\), the quadrilateral IYBX is a cyclic quadrilateral, so \(\angle XIY = 180^\circ - \angle XBY = 180^\circ - 80^\circ = 100^\circ\).

Now, since \(IX\) and \(IY\) are both radii of a circle, \(\triangle IXY\) is isosceles. Using this information, we can find the size of \(\angle IYX\). Then just note that \(\angle AYI = 90^\circ\), and add that to \(\angle IYX\). You will get \(\angle AYX\) that way, which is the required angle.

Can you take it from here?

\(3x + 7 \equiv 2 \pmod{16}\\ 3x \equiv -5 \pmod{16}\\ 33x \equiv -55 \pmod{16}\\ x \equiv 9 \pmod{16}\)

Now you just take x = 9, then calculate the value of 2x + 11 + 4x. The answer is the remainder when 2x + 11 + 4x is divided by 16.

We can use the trailing zeroes trick. 

We can divide 25! by each power of 5. 

25/5=5. But since we don't include the first multiple of 5, there would be four fives. So this would get 4 zeroes.

Now we can divide by 25, or 5^2. This gets an additional one more zero.

This then gets 5 trailing zeroes.

Consider the area of triangle ABC. It can be calculated two different ways.

\(\text{Area of }\triangle ABC = \dfrac{AD \times BC}2 = \dfrac{AC \times BE}{2}\)

So, by simplifying and substituting the values, we actually have \(5\times 18 = 10 \times BE\). That means BE = 9, not 15/2 which Guest suggested.

We need to list all the inequalities and solve the system of inequalities.

Let $x be the amount of the original pile of money.

Then \(\begin{cases}x \geq 200\\80 + \dfrac{4(x - 80)}5 > \dfrac{4x}5\end{cases}\).

Now it is your turn to solve each inequality and find the range of values of x so that both inequalities are satisfied.

This is asked so many times. Please see this thread for the answer: https://web2.0calc.com/questions/floor-function_20#r1

By similar triangles,

\(\dfrac{AB}{AC} = \dfrac{AS}{AT}\\ \dfrac{AT + BT}{AC} = \dfrac{AS}{AT}\\ AS = \dfrac{AT(AT + BT)}{AC} = \dfrac{11(11 + 9)}{35} = \boxed{\dfrac{44}7}\)

Actually, we can ignore the walking distances of the people living at A and E, because their walking distance, no matter where the point is, must add up to 14. Also, it is not optimal to place the point P between A and B or between D and E, because either the person living at B or the person living at D would have to walk a whole lot. We conclude that the optimal location of the point P must be somewhere between B and D. Using the same logic, the walking distances of the people living at B and D can actually be ignored because in that case, it would always add up to 6. We only need to care about how much the person who lives in C needs to walk. Therefore, the optimal strategy is to place the point P at C (i.e., all the friends meet at C). Then AP is just AC, which is 9.

k=14

Explanation:

First, put the like terms on the same side. 6a+4b=k-4b turns into 6a+8b=k

Then you can multiply the top equation by 2 to get 6a+8b=14

Now, you have the system of linear equations, 

{6a+8b=14,

{6a+8b=k

Therefore, k must be equal to 14.

y varies inversely as sqrt(x) means that y = k / sqrt(x) for some non-zero constant k.

Substitute x = 2 and y = 4 into y = k / sqrt(x),

\(4 = \dfrac k{\sqrt 2}\\ k = 4 \sqrt 2\)

So k is 4 * sqrt(2). When y = 16 and k = 4 * sqrt(2), we have 

\(16 = \dfrac{4\sqrt 2}x\\ \)

Can you take it from here?