All Answers 358108 Answers

Ok, so the function is not in the simplest form yet, let's simplify it.

Note that \(\arctan a + \arctan b = \arctan \left(\dfrac{a + b}{1 - ab}\right)\), so we have:

\(\arctan x + \arctan(1 - x) = \arctan\left(\dfrac1{1 - x(1 - x)}\right) = \arctan\left(\dfrac1{x^2 -x +1}\right)\)

What is the range of \(\dfrac1{x^2 - x + 1}\)? We can find that by completing the squares: 

\(x^2 - x + 1 = \left(x - \dfrac12\right)^2 + \dfrac34\\ \), so the range of x^2 - x + 1 is \(\left[\dfrac34, \infty\right)\).

Therefore, it means that the range of \(\dfrac1{x^2 - x + 1}\) is \(\left(0, \dfrac43\right]\).

(If you don't understand interval notations, that means \(\dfrac34 \leq x^2 - x + 1\) and \(0<\dfrac1{x^2 -x + 1} \leq \dfrac43\).)

Note that arctan is a strictly increasing function. As \(0<\dfrac1{x^2 -x + 1} \leq \dfrac43\), we have \(\arctan 0 < \arctan\left(\dfrac1{x^2 - x + 1}\right) \leq \arctan\left(\dfrac43\right)\), so \(0 < \arctan\left(\dfrac1{x^2 - x + 1}\right) \leq \arctan\left(\dfrac43\right)\)

The range of the function is \(\left(0, \arctan\left(\dfrac43\right)\right]\).

We have the inequality: \({2w \over 12 + w} \le {13 \over 20}\), where \(w\) represents the amount of weeks that have gone by (excluding the original 4)

Cross multiplying, we get: \(40 w \le 156 + 13w\).

Now, we have to solve for \(w\) and add 4 to the remaining result. 

Can you take it from here?

You can repeat my calculations 2 more times on your own, but here's how to do the first replacement of solutions:

After 25 gallons are drained, there are 75 gallons of solution with 50% alcohol. That means half of them is alcohol and half of them is other things. So we have 37.5 gallons of alcohol in the tank if you multiply 50% by 75 gallons. 

Now we pour the 25 gallons of 40% alcohol into the tank. That is actually 25(40%) = 10 gallons of extra alcohol and 25 gallons of extra total solution, so we have 100 gallons of solutions again, but the new concentration of alcohol is \(\dfrac{37.5 + 10}{100} \times 100\% = 47.5\%\) instead.

Can you repeat this process twice on your own? If you didn't understand the method, you can ask under this comment.

Similar problem here: https://web2.0calc.com/questions/modular-number-theory_1#r1

Try to solve this problem using the method explained in that thread.

So, suppose the digits were \(a_1, a_2, \cdots , a_{10}\) and a_1 is the first digit, a_2 is the second digit, etc.

Note that the first digit can't be 0. So the required number is 

\((\#\text{ of cases where }a_1 + a_2+ \cdots + a_{10} = 15) - (\#\text{ of cases where }a_2 + a_3 + \cdots + a_{10} = 15)\)

Suppose you mean the exponents form a geometric sequence.

Just combine the exponents using the formula \(a^m a^n = a^{m+n}\).

\(2^{1/3} \cdot 2^{1/9} \cdot 2^{1/27} \cdots = 2^{1/3 + 1/9 + 1/27 + \cdots}\)

Note that the exponent is now the sum of a geometric sequence. Can you complete it now?

Suppose that m is the smallest positive integer such that m! is a multiple of 4125.

First we need to take a look at what 4125 really is. 

\(4125 = 3 \times 5^3 \times 11\)

So, is 11! a multiple of 4125? No, because if you expand 11! = 11 * 10 * 9 * ... * 1, you will notice only 5 and 10 has a factor of 5, so the exponent of 5 in the prime factorization of 11! is 2, not 3. We need another multiple of 5 in the factorial so to make it 3. Therefore, m = 15.

Can you try to find the value of n on your own?

So we have: \(\large{3 \over {4 + { 1 \over {3 + {2 \over 5}}}}}\)

Working our from the bottom, we have: \({4 + {1 \over {17 \over 5}}}\).

The fraction can be simplified to: \(\large{{5 \over 5} \over {17 \over 5}}\)

Because both have a common denominator of 5, we can cancel them out, and we have: \(\large{5 \over 17}\)

This means that the denominator becomes \(4 + {5 \over 17}\), not \(4 + {17 \over 5 }\).

Let the quadratic be in the form \(ax^2 + bx +c\).

Subsituting in \(x = 0\) gives us: \(0a + 0b + c= 3 \), or effectively, \(c = 3\)

Subsituting in \(x = 1\) and \(c = 3\) gives us: \(a + b + 3 = -5\)

Repeating the same process for \(x = 2\) gives us: \(4a + 2b + 3 = 7\)

Now, we have to solve for a and b, and subsitute these into the original quadratic. 

Can you take it from here?

2 + 3 + 7 + 2 + 3 + 7

7 + 3 + 7 + 7

2 + 3 + 3 + 3 + 2 + 2 + 3 + 3 + 3

3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 

2 + 2 + 7 + 2 + 7 + 2 + 2

2 + 2 + 3 + 2 + 2 + 2 + 2 + 2 + 7

3 + 3 + 2 + 3 + 3 + 3 + 7

3 + 2 + 2 + 2 + 2 + 3 + 2 + 2 + 2 + 2 + 2

8 ways 

\(a+b=7\)

\((a+b)^2=7^2\)

\(a^2+2ab+b^2=49\)

\((a+b)^3=7^3\)

\(a^3 + 3a^2b+3ab^2+b^3=343\)

\(3a^2b+3ab^2=301\)

\(a^2b+ab^2=\frac{301}{3}\)

\(ab(a+b)=\frac{301}{3}\)

\(ab(7)=\frac{301}{3}\)

\(ab = \frac{43}{3}\)

\(a^2 + 2ab + b^2 = 49\)

\(a^2 + \frac{86}{3} + b^2 = 49\)

\(a^2 + b^2 = 49 - \frac{86}{3} \)

\(a^2 + b^2 = \boxed{\frac{61}{3}}\)

nvm solved it by the way the answer is 9

But what's the answer

Here is you diagram, can you work it out now.

\(3^0=1 \;\;(base10)\;\;\equiv 1 \;\;(base16)\;\; \\ 3^1=3 \;\;(base10)\;\;\equiv 3 \;\;(base16)\;\; \\ 3^2= \;\;(base10)\;\;\equiv 9 \;\;(base16)\;\; \\ 3^3=27 \;\;(base10)\;\;\equiv B \;\;(base16)\;\; \\ 3^4=81 \;\;(base10)\;\;\equiv 51 \;\;(base16)\;\; \\ \)

The pattern for the last digit is now set.

\(3^{0+4n} \;\;ends \;\;in\;\; 1 \;\;(base16)\;\; \\ 3^{1+4n} \;\;ends \;\;in\;\; 3 \;\;(base16)\;\; \\ 3^{2+4n}\;\;\;\;ends \;\;in\;\; 9 \;\;(base16)\;\; \\ 3^{3+4n} \;\;\;\;ends \;\;in\;\;B \;\;(base16)\;\; \\ \)

2019 = 4*504+3

So 

\(3^{2019}\quad \text{has a unit digit of WHAT in base 16.}\)

** Please give a response

The set of all real numbers x

so that \((x^2\leq3)\ is\ \color{blue}x\in\mathbb R\ |\ -\sqrt{3}\leq x\leq +\sqrt{3}.\)

  !

 What is the ratio of Emily's money to Cindy's?

Hello Guest!

\(e=\frac{2c}{7}\\ e+\frac{c}{7}=\frac{6c}{7}-30\\ e=\frac{5c}{7}-30\\ \frac{2c}{7}=\frac{5c}{7}-30\\ -\frac{3c}{7}=-30\\ \color{blue}c_{start}=70\)

\(e=\frac{2}{7}c\\ \color{blue}e_{start}=20\)

\(\frac{e+\frac{c}{7}}{\frac{6c}{7}-30}=\frac{20+10}{60-30}=\color{blue}\frac{1}{1}\)

The ratio of Emily's money to Cindy's is 1 : 1.

  !

What is x when r = 25?

Hello Guest!

\(x:r=5:40\\ x=\frac{r}{8}=\frac{25}{8}=\color{blue}3.125\)

   !

Hi Ginger.  What a delight to hear from you again.  And educational too – well, that's what happens on this site – I didn't know that horses' teeth continue growing throughout their lifetimes.  I did know that sharks' teeth replenish themselves ... when one breaks off, a replacement rolls up from underneath, kind of like a box of Kleenex.  I don't describe myself as long in the tooth; I prefer old and in the way.  Ron  

_.

3^2019 mod 10^10==4B5998A3F1C1AAA3 - these are the 10 "digits" in base 16

No. of muffins in the afternoon (sold)

  = 600/2 = 300

  let x = total muffins left in

                the afternoon

   300 = 5/6x  ; x = 300/5/6 = 360

total muffins left in the end

    = 360 - 300 = 60

total muffins = 60/1/8 = 480

Money Jaffar received from the morning sale

= (480 - 60 - 300)/4 * $11 = $330

Let

     No of marbles with Ethan = x

     No of marbles Daniel has = y

If Ethan gives 16 marbles to David 

both of them will have equal numner

          ∴ x - 16 = y + 16

              x = y + 16 + 16

               x = y + 32 ---- (1)

If Daniel gives 9 marbles to Ethan

           x + 9 : y - 9

               6   :   1

 Total marbles = x + y (7 parts / units)

         1 unit/part = (x + y)/7

(x + y)/7 * 6 = x + 9        (x + y)/7 * 1 = y - 9

                          ---- (2)

Sub eqn (1) in (2)

(y + 32 + y)/7 * 6 = y + 32 + 9

(6(2y + 32))/7 = y + 41

12y + 192 = 7(y + 41)

12y + 192 = 7y + 287

  12y - 7y = 287 - 192

5y = 95

  y = 95/5 = 19
Sub y = 19 in eqn (1)

   x = 19 + 32 = 51

Total marbles = x + y

                      = 51 + 19

                      = 70

Simplify the second equation to: \(6a+8 b=k\).

For a system of equations to have infinite solutions, the two equations must be a multiple of each other. 

Note that the second equation is twice the first equation. 

Can you take it from here?

continued here 

Yes it is 13/25     (Max I think you made a small error)

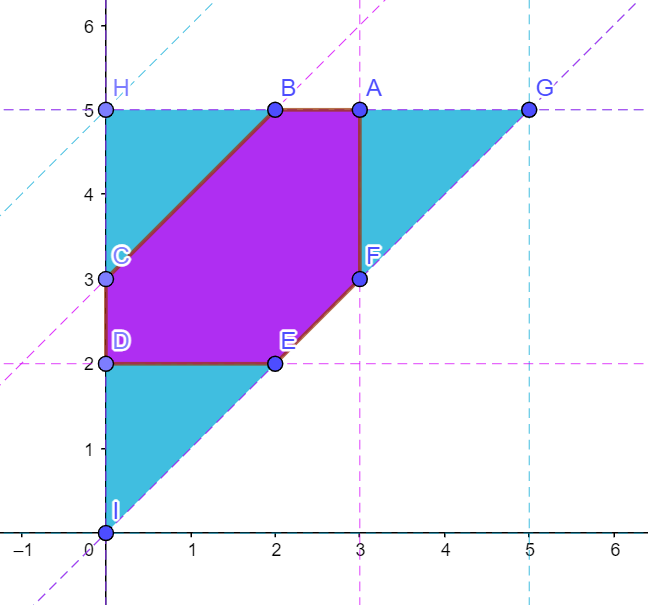
Here is my contour probability  graph