All Answers 358180 Answers

Well, for #2, I calculated in the exact same manner as you did. I multiplied 5 by 2 first. However, order of operations says that you always calculate from left to right. I didn't do that. 

I guess that note causes more confusion that what is intended...

This calculator has a limit of 199! Anything above that, it will say "infinity".

However, yours can be reduced to this:

365! / (335! * 365^30) =365 - 335 =30.

 [365P30] / 365^30=0.29368375728073........etc.

If by "use properties" you mean find a way to do these in your head, here's my take:

93 + 68 + 7                  The 93 and the 7 sum to 100

=  100 + 68

=  168

5 * 23 * 2                      5 and 2 multiply to 10

=  10 * 23                     To multiply by 10, move the decimal point right one position.

=  230

8 * 51

=  8 * (50 + 1)

=  8 * 50 + 8 * 1

=  8 * 5 * 10 + 8 * 1

=  40 * 10 + 8

=  400 + 8

=  408

34 + 0 + 18 + 26           The 34 and 26 sum to 60

=  60 + 18

=  78

6 * 107

=  6 * (100 + 7)

=  6 * 100 + 6 * 7

=  600 + 42

=  642

I only used the calculator to check these! 

Also...here is a question for X² ....why did you say that calculating in this fashion doesn't adhere to the order of operations ?

1. \(93+(68+7)=93+75=168\)

2. \(5*23*2=23*10=230\)

Although calculating in this fashion does not adhere to the order of operations, calculating it this way makes it easier mentally. I can use this method because of the commutative property of multiplication, which states that multiplication can be done in any order

3. \(8*51=408\)

4. \(34+0+18+26=34+18+26=52+26=78\)

5. \(6*107=642\)

Except for #2, I use order of operations to calculate the sum or product. For number 2, I utilized the commutative property of multiplication.

That's OK, X²......your explanation was better than mine....

If the sewing machines are independent of each other, then the number of shirts is proportional to number of sewing machines x  time. So,

5 : 5 x 5, or:

5 shirts/[5 machines x 5 minutes] = 1 shirt per 1 machine in 5 minutes.

5 /[5 x 5] = 100/[100 x M], and 

M = 5 minutes - so takes 5 minutes for 100 sewing machines to make 100 shirts.

This is a linear function.

A linear function is a type of function where its resulting graph is a straight line. Linear functions have a standard form.

\(f(x)=mx+b\)

f(x) is the same thing as y.

m is the slope of the function

b is the y-intercept.

We can rearrange the above equation, \(y=10000+350x\) into that form. Just swap the terms on the right side of the equation

\(y=350x+10000\)

In the above equation, we have defined all the terms; the slope, m, is 350, and the y-intercept is 10000. Therefore, this is a linear function.

Well, I would have supplied the link to a graph, but Cphill beat me to it already...

Definitely, linear....here's the graph :

https://www.desmos.com/calculator/g6zznwsare

Accessing the inverse cosine function is relatively simple.

Step 1: Click the 2nd Button

In the top left corner of the calculator window, click the 2nd button. Clicking this allows a user to access secondary functions.

Step 2: Click the acos Button

The acos and the cos^-1 are the same thing. A parenthesis will show up. Npw, input what number you'd like to apply the inverse cosine function to.

Step 3: Close Parenthesis

For proper syntax, close the parenthesis after inputting what number you'd like to input.

Step 4: Click the "=" Button

Clicking this will make the calculator do the calculation. You're done! YEAH

\(\frac{23}{99}\) is a fraction already in simplest form. 

The question is solved, and you are safe. Do not worry :)

Each minute, 1 shirt is made by 5 machines......so 100 machines must be able to make 20 times as many in one minute = 20 shirts in one minute.....so....it must take 5 minutes for 100 machines to make 100 shirts 

I have 3 pieces of candy to place in 4 lunch boxes. In how many ways can I do this if:

(a) The candies are all different and the lunch boxes are all different?
Say the lunch boxes are red, blue and yellow and the  candies are X,Y,Z

(b) The candies are all the same and the lunch boxes are all the same?
3 in 1 and none in the others

2 in one box and 1 in another

1 in each box

6 ways

(c) The candies are all the same and the lunch boxes are all different?

(d) The candies are all different and the lunch boxes are all the same?

(e) Exactly two of the candies are the same (but the third is different) and all of the lunch boxes are different?

That is what I get :/   My answers should be checked though :)

Thank you Heureka,

Now I am very happy :))

\(\text{The first solution that comes to mind is choosing }n=7\\ \text{and }k=2\text{. This allows the product }mn\text{ to consist of}\\ \text{even powers which results in a natural number when }\\ \text{taking the second power root. Now we need to check if}\\ \text{this solution is indeed the smallest possible value for }n.\\ \text{We know that a smaller solution can be acquired only}\\ \text{if we don't need to add an extra factor 7. This requires}\\ \text{343 being divisible by }k\text{. We know }343=7^3\text{ so }k\text{ must}\\ \text{equal some power of 7 for this to be the case. 1980 and}\\ \text{384 are not divisible by 7, 1694 however is. To correct for}\\ \text{this }n\text{ needs to equal 6 (because 1981 and 385 are divisible}\\ \text{7). As 6 is smaller than 7 are solution becomes: }n=6,\\ k=7;n+k=13.\\ \text{If this explanation is still a bit hazy, allow me to show it in}\\ \text{formula form:}\\ \)

\(n=2^\alpha\cdot3^\beta\cdot5^\gamma\cdot7^\delta\Rightarrow\\ mn=2^{1980+\alpha}\cdot3^{383+\beta}\cdot5^{1694+\gamma}\cdot7^{343+\delta}\Rightarrow\\ 2^{\frac{1980+\alpha}k}\cdot3^{\frac{383+\beta}k}\cdot5^{\frac{1694+\gamma}k}\cdot7^{\frac{343+\delta}k}\in\mathbb{N}\Rightarrow\\ \frac{1980+\alpha}k,\frac{383+\beta}k,\frac{1694+\gamma}k,\frac{343+\delta}k\in\mathbb{N}.\)

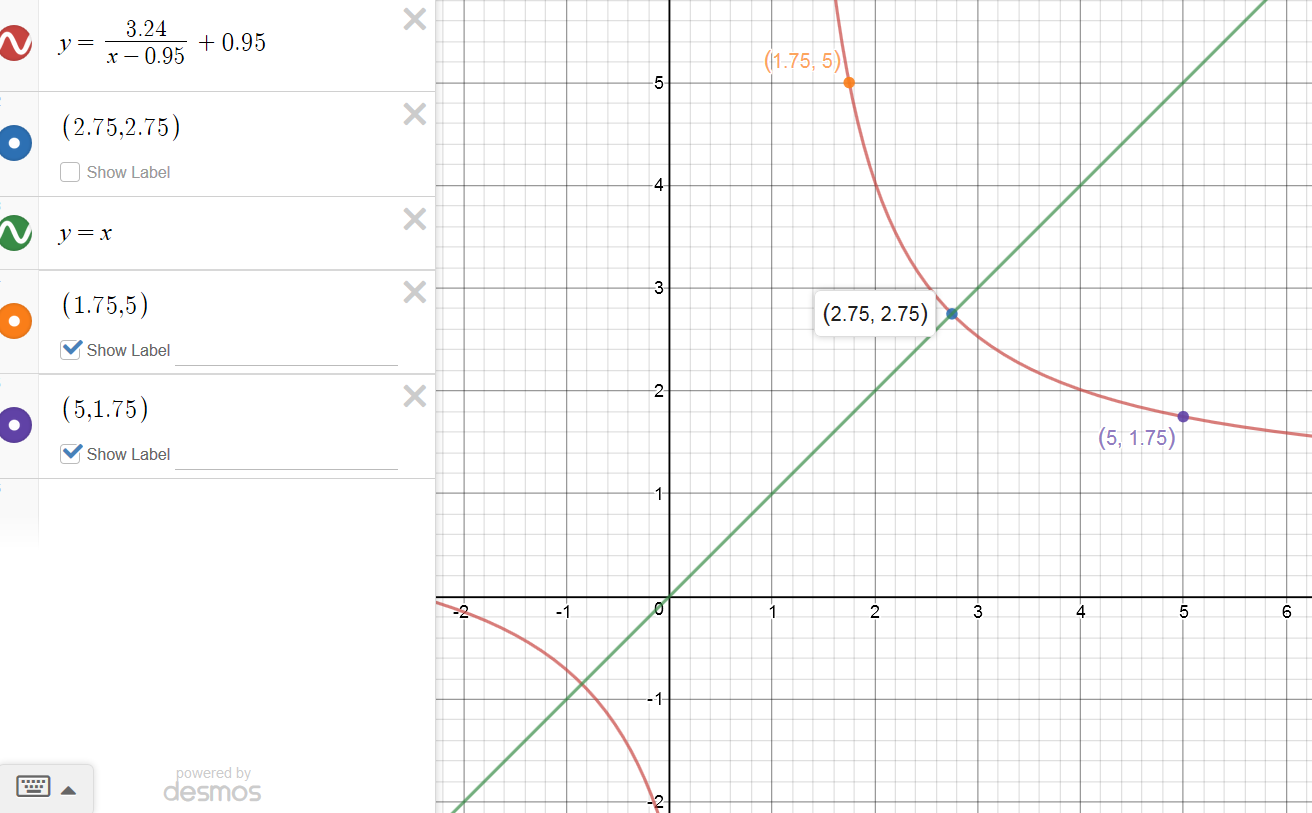
I think it goes through the points (2.75,2.75) (1.75,5) and (5,1.75)

How do I find a graph that will go through these points ?? 

The formula of a hyperbola is given in general form: \(y = \frac{a}{x+c} + d \)

Set \(P_1(x_1,y_1) = (2.75,2.75)\)
Set \(P_2(x_2,y_2) = (1.75,5)\)
Set \(P_3(x_3,y_3) = (5,1.75)\)

\(\begin{array}{|lrcll|} \hline (1) & y_1 &=& \frac{a}{x_1+c} + d \\ & (y_1-d)*(x_1+c) &=& a \\ & y_1x_1+cy_1-dx_1&=& a+cd \\\\ (2) & y_2 &=& \frac{a}{x_2+c} + d \\ & (y_2-d)*(x_2+c) &=& a \\ & y_2x_2+cy_2-dx_2&=& a+cd \\\\ (3) & y_3 &=& \frac{a}{x_3+c} + d \\ & (y_3-d)*(x_3+c) &=& a \\ & y_3x_3+cy_3-dx_3&=& a+cd \\\\ \hline \end{array} \)

\(\begin{array}{|lrcll|} \hline (1) & y_1x_1+cy_1-dx_1&=& a+cd \\ (2) & y_2x_2+cy_2-dx_2&=& a+cd \\ (3) & y_3x_3+cy_3-dx_3&=& a+cd \\ \hline (1)-(2) & y_1x_1+cy_1-dx_1 -(y_2x_2+cy_2-dx_2) &=& 0 \\ & c(y_1-y_2)+d(x_2-x_1) &=& y_2x_2-y_1x_1 \\\\ (1)-(3) & y_1x_1+cy_1-dx_1 -(y_3x_3+cy_3-dx_3) &=& 0 \\ & c(y_1-y_3)+d(x_3-x_1) &=& y_3x_3-y_1x_1 \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline (1) & c(y_1-y_2)+d(x_2-x_1) &=& y_2x_2-y_1x_1 \\ (2) & c(y_1-y_3)+d(x_3-x_1) &=& y_3x_3-y_1x_1 \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline c &=& \frac{ \begin{vmatrix} y_2x_2-y_1x_1 & x_2-x_1 \\ y_3x_3-y_1x_1 & x_3-x_1 \end{vmatrix} } { \begin{vmatrix} y_1-y_2 & x_2-x_1 \\ y_1-y_3 & x_3-x_1 \end{vmatrix} } \\ c &=& \frac{ \begin{vmatrix} 5\cdot1.75-2.75\cdot2.75 & 1.75-2.75 \\ 1.75\cdot5-2.75\cdot2.75 & 5-2.75 \end{vmatrix} } { \begin{vmatrix} 2.75-5 & 1.75-2.75 \\ 2.75-1.75 & 5-2.75 \end{vmatrix} } \\ \mathbf{c} &\mathbf{=}& \mathbf{-0.95} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline d &=& \frac{ \begin{vmatrix} y_1-y_2 & y_2x_2-y_1x_1 \\ y_1-y_3 & y_3x_3-y_1x_1 \end{vmatrix} } { \begin{vmatrix} y_1-y_2 & x_2-x_1 \\ y_1-y_3 & x_3-x_1 \end{vmatrix} } \\ d &=& \frac{ \begin{vmatrix} 2.75-5 & 5\cdot 1.75-2.75\cdot 2.75 \\ 2.75-1.75 & 1.75\cdot 5-2.75\cdot 2.75 \end{vmatrix} } { \begin{vmatrix} 2.75-5 & 1.75-2.75 \\ 2.75-1.75 & 5-2.75 \end{vmatrix} } \\ \mathbf{d} &\mathbf{=}& \mathbf{0.95} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline a &=& y_1x_1+cy_1-dx_1-cd \\ a &=& 2.75\cdot 2.75-0.95\cdot 2.75-0.95\cdot 2.75 - (-0.95)\cdot 0.95 \\ \mathbf{a} &\mathbf{=}& \mathbf{3.24} \\ \hline \end{array}\)

The formula of a hyperbola is given through  \(P_1, P_2, P_3:\ y = \frac{3.24}{x-0.95} + 0.95\)

The graph is:

Nice CPhill  !! This was harder than it first looks, for me at least !  Here is just the factoring part. I did it at first just to see it for myself, and then I figured it couldn't hurt to post it.

cos x  +  6 sin²x  -  2 sin x cos x  -  3 sin x   =   0        Rearrange.

6 sin²x  -  3 sin x  +  cos x  -  2 sin x cos x   =  0         Factor out  3 sin x  from the first two terms and

                                                                                     factor out  -cos x  from the last two terms.

3 sin x (2 sin x - 1)  -  cos x (-1 + 2 sin x)  =  0             Factor out  (2 sin x - 1)  from both terms.

(2 sin x - 1)(3 sin x - cos x)  =  0

Can't understand your question with all those $$ signs !!.

cot x + 6 sin x - 2 cos x =3     we can write

cosx / sinx  +  6sin x - 2 cosx  = 3       multiply through by sin x

cos x  +  6 sin^2x  -  2cosx sin x  =  3sin x

cos x + 6sin^2x  - 2sin cos x  - 3sin x  = 0         we can factor this as

( 3sinx  - cosx) (2sinx  - 1) = 0      set each factor to 0  and solve

3sinx  - cos x  = 0  

3sin x  = cos x

3sinx / cos x  =  1

3 tan x  =  1

tan x  = 1/3 

arctan (1/3)  ≈  18.435°  + 180°n    where  n is an intreger

For the other factor we have that

2sinx - 1  = 0

2sin x  = 1

sin x  =  1/2     

arcsin (1/2)    and this happens at  30° + 360°n    and at  150° + 360°n

And again, n is an integer

Here's ther graph : https://www.desmos.com/calculator/eiai1cs0i1

tan (pi /6)  =  1 / √3   =  √3 / 3

First, let's draw an equilateral triangle where the sides are length  n  and the angles are  pi/3  .

Second, draw a line that bisects the angle. Since the other two sides are the same length, it also bisects the opposite side and forms a right angle. This forms the angles   (pi/3)/2  =  pi/6

Now, let's look at this third triangle. Let's call the length of the remaining side  " a " .

We can find  " a "  using the Pythagorean theorem.

a² + (n/2)²  =  n²

a  = \(\sqrt{n^2-(\frac{n}{2})^2}=\sqrt{\frac{4n^2-n^2}{4}}=\frac{\sqrt3n}{2}\)

tan( pi/6 )  =  opposite / adjacent  =  \(\frac{n}{2}\,/\,\frac{\sqrt3n}{2}=\frac{n}{2}\,*\,\frac2{\sqrt3n}=\frac1{\sqrt3}=\frac{\sqrt3}{3}\)

No calculator needed !  

For more of an explanation to your first and second question. The first question means when you have a function and (x) approaches (a) from the left side (that's why there is a negative sign). You are trying to determine what the function is behaving as (x) approaches (a) from the left. The same applies for positive, however, as you might imagine you'll try to determine from the right as (x) approaches (a). This is important in respects to school knowledge as a function may not behave the same on the negative side of a as (x) approaches (a) and vice versa for the positive side. That's why there is a proof to graph a function where the behavior is different as (x) approaches (a) from the left (negative) and right side (postive) so you'll be able to understand this concept (if you haven't by the time of this post).

I solved my question !!!!!

I thought it over in my head cuz' 3/3/3/3 = 1/9

Then I realized it's either 1/x^(sqrt(y)) or 1/x^(y/2) or 1/x^(y-2)

The 3^rd one is correct. The calculator simplified it to x^(2-y)