I am going to give an alternate answer for Question 2
First I need to examine some properties of rectangles
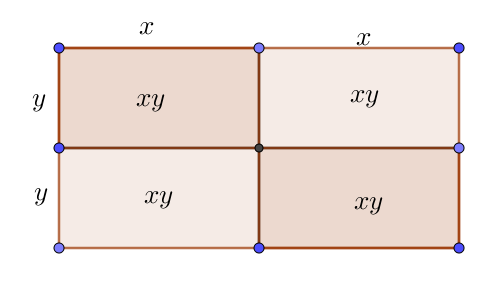
First I will put in the 2 axes of symmetry of a rectangle. The diagram is below;
It can be seen that the area of the whole rectangle is \(2x*2y=4xy\;\;\;units^2\)
The sum of the diagonally opposite rectanges inside it is \(xy+xy=2xy=\dfrac{ \text{total area}}{2}\)
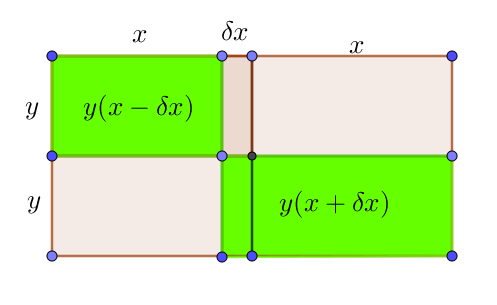
Now what happens if one of the dividing lines is an axis of symmetry but the other is moved over a little bit ? See diagram below
The total area is still \(4xy\;\;\;units^2\)
The sum of the diagonally opposite (green)rectanges inside it is
\(y(x+\delta x)+y(x-\delta x)=2yx=\dfrac{\text{total area}}{2}\\ \text{Which is still the same as before.}\)
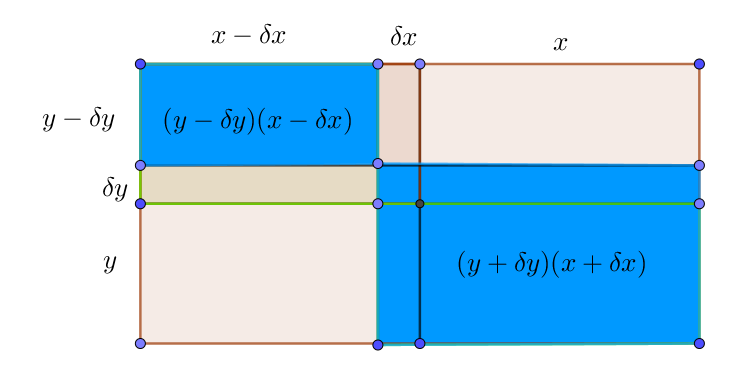
So what happens if BOTH dividers are moved away from the axis of symmetry?
See diagram below:
The total area is still \(4xy\;\;\;units^2\)
The sum of the diagonally opposite (blue) rectanges inside it is
\((y+\delta y)(x+\delta x)+(y-\delta y)(x-\delta x)\\ =yx+y(\delta x)+x(\delta y)+(\delta x)(\delta y)\quad+\quad yx-y(\delta x)-x(\delta y)+(\delta x)(\delta y)\\ =2yx+2(\delta x)(\delta y)\\ \ne \dfrac{\text{total area of rectangle}}{2}\\ \)
So what I have shown here is that if a rectangle is divided into 4 using 2 intervals, one inteval parallel to each of the sides. Then the sum area of the diagonally opposite internal rectangles will be equal to half the area of the whole rectangle IF AND ONLY IF on of the intervals is an axis of symmetry of the original rectangle.
[maybe this could be worded better  ]
]
----------------------------------------------------------------------
So lets look at the actual question 2 now!
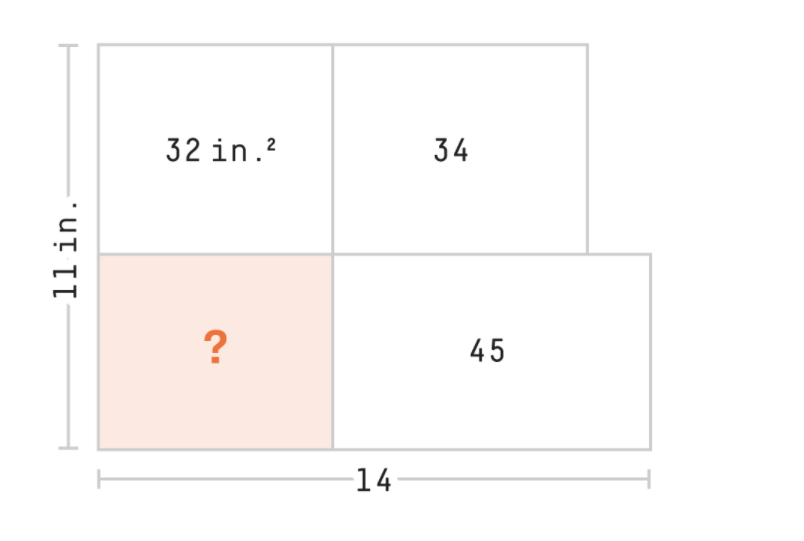
Total area = 11*14 = 154 inches squared
1/2 of totall area = 77 inches squared
45+32=77 inches squared
SO one of those dividing lines MUST be an axis of symmetry of the whole rectangle.
So the question mark must equal either 45 or 32
Area of the known peices is 32+34+45 = 111 Area unaccounted for = 154-111= 43
So the question mark area must be smaller than 43.
Hence the question mark area is 32 inches squared.
