Before starting any problems listed above, you should understand what a similar polygon means. In general, it means that all corresponding angles in two figures are congruent and that all corresponding sides are proportional. Proving corresponding sides proportional requires that you find the ratio of corresponding sides and check for equality.
11)
In this example, both figures are rectangles, so every angle is a right angle. All right angles are congruent. The next step requires us to compare the ratio of the sides.
\(\frac{20}{40}\stackrel{?}=\frac{24}{48}\)
Notice what has happened here. For the smaller rectangle, the leftward fraction represents the ratio of the shorter side of the smaller rectangle to the longer side. The ratio is the same for the larger rectangle. Both fractions can be simplified.
\(2=2\)
The ratios are the same, so both rectangles are similar polygons.
12)
For this problem, simply employ the same strategy as before. The figures are rectangles, so it is already established that the angles are congruent. Now, let's compare the ratios of corresponding sides.
\(\frac{8}{16}\stackrel{?}= \frac{12}{30}\\ \frac{1}{2}\neq \frac{2}{5}\)
After simplifying both fractions to simplest terms, it becomes clear that the ratio of corresponding side lengths is not proportional. By definition, corresponding side lengths must be proportional in order for two figures to be considered similar. Since this is not the case, these rectangles are not similar.
13)
The diagram is not the prettiest work because I cannot figure out how to show congruent angles on this program. I used slipshod cut-off semicircles.
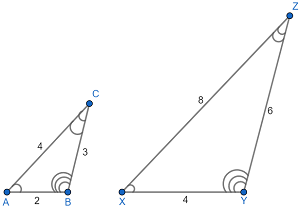
In the diagram above, \(\angle A\cong \angle X\text{ and }\angle B\cong \angle Y\text{ and }\angle C\cong\angle Z\). Also, \(\frac{2}{4}=\frac{3}{6}=\frac{4}{8}\), so \(\triangle ABC\sim\triangle XYZ\).
14) The beauty of a similarity (or congruence) statement is that it reveals more information than it may first appear. We should not forget what similarity means! Let's look at the individual choices.
\(m\angle C=m\angle Z\) is true because both letters appear in the same position in the similarity statement \(\triangle AB\textcolor{red}{C}\sim\triangle XY\textcolor{red}{Z}\). Corresponding angles are always congruent in similar triangles.
\(\frac{\textcolor{red}{AB}}{\textcolor{red}{XY}}=\frac{\textcolor{blue}{YZ}}{\textcolor{blue}{BC}}\) is not true! Notice that \(\triangle \textcolor{red}{AB}C \sim \triangle \textcolor{red}{XY}Z\text{ and }\triangle A\textcolor{blue}{BC}\sim\triangle X\textcolor{blue}{YZ}\). Remember that both ratios must compare a pair of corresponding sides. In the leftward statement, it compares a side of the smaller triangle to a corresponding side of the larger triangle. In the rightward statement, the ratio compares the length of the larger triangle to the shorter one. Notice how the similarity statement shows this discrepancy; notice that the letters are not in the same order.
\(AB\cong XY\) is not true. Yes, it lines up with the similarity statement \(\triangle \textcolor{red}{AB}C \sim \triangle \textcolor{red}{XY}Z\), but corresponding sides are proportional--not congruent.
\(\frac{\textcolor{red}{BC}}{\textcolor{red}{YZ}}=\frac{\textcolor{blue}{AC}}{\textcolor{blue}{XZ}}\) is true because it matches perfectly with the similarity statement. Notice that \(\triangle A\textcolor{red}{BC}\sim\triangle X\textcolor{red}{YZ}\) and \(\triangle \textcolor{blue}{A}B\textcolor{blue}{C}\sim\triangle \textcolor{blue}{X}Y\textcolor{blue}{Z}\).
15)
6-8-10 and 9-12-15 are a special set of numbers known as Pythagorean triples, which are positive-integer side lengths of a right triangle. Since both side lengths have this property, we can conclude that \(m\angle B=m\angle F= 90^\circ\). An accepted method of proving triangles similar is called Side-Angle-Side Similarity Theorem, which states that the one pair of sides is proportional, and the included angle is congruent.
\(\frac{6}{8}\stackrel{?}=\frac{9}{12}\\ \frac{3}{4}=\frac{3}{4}\)
The side lengths are proportional, so we can conclude, by the Side-Angle-Side Triangle Similarity Theorem, that \(\triangle ABC\sim\triangle DFE\).