All Answers 356765 Answers

I'll show you how to find the after-image point for one point, Kyinx.....you can figure the other three from this....

After-image point =   [ old point - center of dilation ] *scale factor + dilation center

So.....to find the new after-image point for the point (-1, 1)  we have

[ (-1, 1) - (-7, -2) ] * 2   + (-7, - 2)     =

[ 6, 3] *2   + (-7, -2)   =

(12, 6) + (-7, -2)  =

(5, 4)

Use the same proceedure for each of the other three points on the graph above

5.  An isosceles trapezoid has side lengths 13,3,13 and 14. What is the perimeter of its Varignon parallelogram?

I didn't actually know what a Varignon parallelogram was.....the parallelogram is formed by joining the midpoints of the sides of the trapezoid...

See the image below :

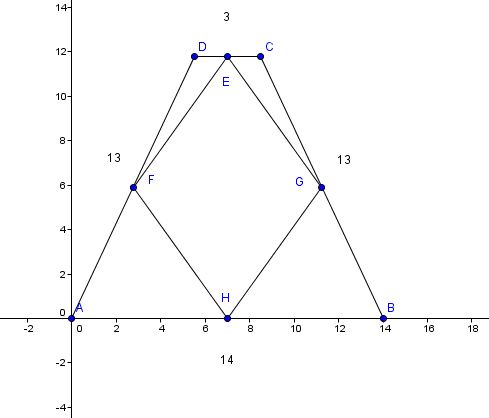
EFGH is the Varignon parallelogram

A = (0,0)

B = (14,0)

The height of the trapezoid is  sqrt (13^2 - 5.5^2] = sqrt (138.5)

C = (8.5, sqrt (138.75) )

D = (5.5, sqrt (138.75) )

In this case, the sides of the parallelogram are congruent....so....we only need to multiply the distance from F to H  by 4 to find ts perimeter

F =  (5.5/2 , sqrt (138)/2 ) =  (2.75, sqrt (138)/ 2 )

H = (7, 0)

So  FH  =    sqrt [  (7 - 2.75)^2 + 138/4 ]   =  sqrt ( 4.25^2 + 34.5) =

sqrt ( 18.0625 + 34.5)  =  sqrt ( 56.5625)  =  7.25

And the perimeter is 4 times this =  4 * 7.25 = 29 units

P.S. - Just wonder if it's a coincidence that the sum of the lengths of the three shortest sides of the trapezoid = the perimeter of the parallelogram????

Are they already answered?

I can answer this when I can access the links in an hour and a half or you can upload images now.

A reflection across y = -x is basically across both axis. So, just change the sign for all of the points.

This site really helped me do this:

https://www.desmos.com/calculator

1.) 1/8pi

1.) The angles are 56, 90 and 34.

\(\text{If there are 8 T's there are 8 C's, so we are left with 14 slots}\\ \text{This means that A=G=7}\\ P[\text{8 T's}] = \dbinom{30}{8}\dbinom{22}{8}\dbinom{14}{7}(0.29)^7(0.23)^8(0.27)^7(0.21)^8\)

Now the problem might actually mean there are at least 8 T's.  In which case we'd modify above to be

\(\large \sum \limits_{t=8}^{15}~\dbinom{30}{t}\dbinom{30-t}{t}\dbinom{30-2t}{15-t}(0.29)^{15-t}(0.23)^t(0.27)^{15-t}(0.21)^t\)

Can see well enough to type in the question!  THAT takes more effort than entering it in the calculator.....

\(24000=(1-0.04)O_{lastyr}\\ O_{lastyr} = \dfrac{24000}{0.96} = 25000\)

Factor 109! =

2^104×3^53×5^25×7^17×11^9×13^8×17^6×19^5×23^4×29^3×31^3×37^2×41^2×43^2×47^2×53^2×59×61×67×71×73×79×83×89×97×101×103×107×109 (260 prime factors, 29 distinct).

= 3^53

got glasses broken yesterday cant see

what is 6-300(82-9)56

6 - (300)(73)56 = - 1226394    Just use a calculator....

1023444444 divided by 23867644

You get  "Silly Question of the Day" award....there is a calculator on this website.....

1023444444 / 23867644 = 42.8799945231293043

Correct....!!!

Not quite, NSS

The legs are YZ and ZX   ⇒  "C"

3)

\(P[A] = \left(1-\dfrac 1 2\right)\left(\dfrac 1 4\right) = \dfrac 1 8\\ P[B]= \text{.... are you supposed to be able to do this w/o software?}\\ \text{It's next to impossible by hand}\\ \text{unless I'm missing some major trick which is certainly possible}\)

Sorry......missed that...

Those questions weren't answered

See this:

https://web2.0calc.com/questions/plz-help-with-math-and-please-explain-asap

2)

\(P[1]=\dfrac 3 5=p,~P[0]=\dfrac 2 5\)

\(P[A]=\dfrac 3 5 \dfrac 2 5 = \dfrac{6}{25}\\ P[B] = \dbinom{8}{4}\left(\dfrac 3 5\right)^4\left(\dfrac 2 5\right)^4 = \dfrac{18144}{78125}\\ P[A \cap B] = \dfrac{6}{25} \dbinom{6}{3}\left(\dfrac 3 5\right)^3\left(\dfrac 2 5\right)^3 = \dfrac{5184}{78125}\)

\(P[A \cup B] = \dfrac{6}{25} + \dfrac{18144}{78125}-\dfrac{5184}{78125}=\dfrac{6342}{15625}\)

\(\text{Let }A=\{\text{string starts with 10}\}\\ B=\{\text{string contains exactly 4 0s}\}\)

1)

\(P[0]=P[1]=\dfrac 1 2\\ \text{P[A] is the probability of selecting 10 out of the 4 possible 2 bit combos}\\ P[A] = \dfrac 1 4\\ P[B] = \dfrac{\binom{8}{4}}{2^8} = \dfrac{35}{128}\\ P[A \cap B] = P[\text{bits 1-2 are 10 and bits 3-8 have 3 0's}] = \\ \dfrac 1 4 \dfrac{\binom{6}{3}}{2^6}=\dfrac{5}{64}\)

\(P[A \cup B] = P[A]+P[B]-P[A \cap B]\\ P[A \cup B] = \dfrac 1 4 + \dfrac{35}{128}-\dfrac{5}{64} = \dfrac{57}{128}\)

More like they are labelled backwards!                 Wanted to be sure Q was posted correctly....

1. Consecutive angles in a parallelogram are supplemental (sum to 180 degrees)

x - y = 40      implies that   x = 40 + y

Thus

 x + y = 180

(40 + y) + y = 180

2y + 40  = 180        subtract 40 from both sides

2y = 140      divide both sides by 2

y = 70°

2.  Area of rhombus =

2 * (1/2) * 6^2 * sin (120)   =   36 sqrt (3)/2 = 18 sqrt(3) units^2

3.       (A) A quadrilateral is a parallelogram if it is a rhombus.