All Answers 357330 Answers

it is not to scale

Sum of interior angles of pentagon = 540 degrees

   540/(2+3+4+4+5) = 30          5 x 30 = 150 degrees largest angle

thank you!

12 x 12 x 12 cm     (1728 cm^3)

1.   Cannot see the graph

2 For every value of  'x' ,  transformed  f(x) will be shifted DOWN two units....so the entire graph will be shifted down two units from the parent graph.

P ( i) t        

  P = principal (or amount of deposit)    i = annual  interest in decimal (ex: 2%  would be i = .02)   t = time in years

1 .    y is much larger than x in the diagram.....how can x-y be positive 40?

2

b^3 - 4b^2 - 21b = 0       Factor out 'b'

b (b^2-4b-21) = 0          factor

b (b-7)(b+3)   = 0   

         for this to = 0     either ( b = 0)      or b-7 = 0    (b=7)     or b+3 = 0   (b=-3)

Pool area is  30 x 12 = 360 ft^2

will be bounded by walkway which is    ( 30 +2w) feet long x two   and  12 feet long x two

The width will be  'w'

(30+2w)(2) + 12(2) ) (w)  =( 1288-360)

(60 + 4w +24)w  = 928 ft^2

60w + 4w^2 + 24w

4w^2 + 84w -928 = 0      Divide by 4

w^2 + 21w - 232 = 0

 Use quadratic formula to find   w = -52/8 (extraneous)   or   8 ft wide

2 (x-3)^2 + 1 = 9    Subtract 1 from both sides of the equation

2(x-3)^2 = 8          Divide both sides by 2

(x-3)^2 = 4             SQRT both sides

x-3 = +-2           Add 3 to both sides

x = 5 or 1 

I forgot to log in before saying that! That was me.

I am having a good day. Yay!

G is the centroid of equilateral Triangle ABC. D, E, and F are midpoints of the sides as shown.
P, Q, and R are the midpoints of Line AG, Line BG, and Line CG, respectively.
If AB=sqrt(3) what is the perimeter of hexagon DREPFQ?

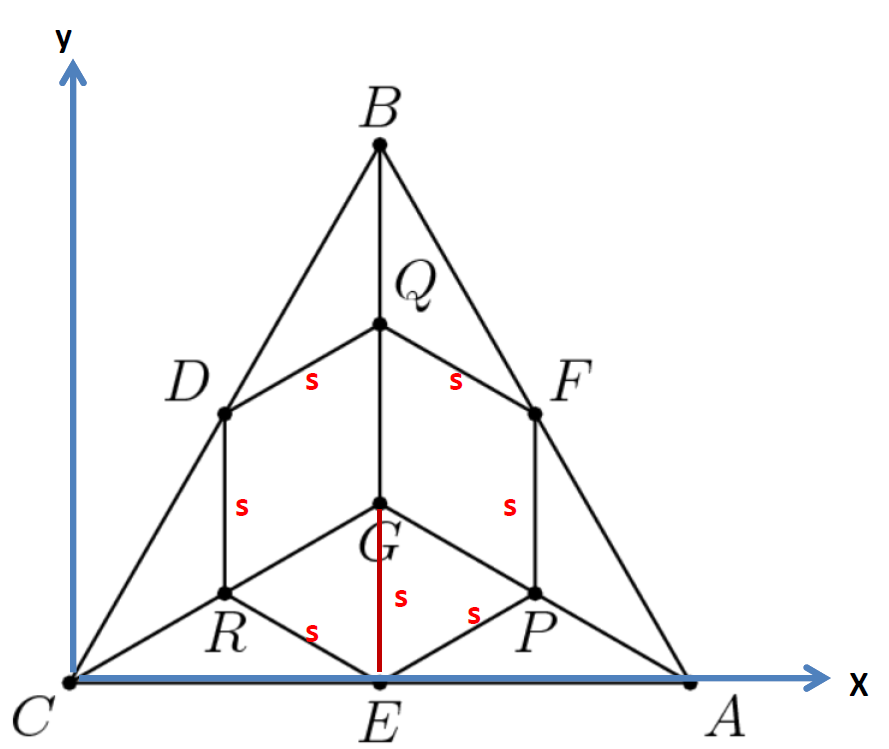
$\text{Let $AB=\sqrt{3}$} \\ \text{Let $CE=\frac12\sqrt{3}$} \\ \text{Let Point $C=(0,0)$} \\ \text{Let Point $A=(\sqrt{3},0)$} \\ \text{Let Point $B=(\frac12\sqrt{3},\frac32)$} \\$

$\begin{array}{|rcll|} \hline BE^2 + \left(\frac12 \sqrt{3} \right)^2 &=& (\sqrt{3})^2 \\ BE^2 &=& 3 - \frac34 \\ BE^2 &=& \frac94 \\ \mathbf{BE} & \mathbf{=} & \mathbf{\frac32} \\ \hline \end{array}$

$\text{Let Point $B=(\frac12\sqrt{3},\frac32)$}$

$\begin{array}{|rcll|} \hline G &=& \left( \frac{0+\sqrt{3}+\frac12\sqrt{3}}{3}, \frac{0+\sqrt{0}+\frac32}{3} \right) \\ G &=& \left( \frac12\sqrt{3}, \frac12\right) \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline s &=& \frac12 \\ \text{perimeter}_{\text{of hexagon }DREPFQ} &=& 6s \\ &=& 6\cdot \frac12 \\ &\mathbf{=}& \mathbf{3} \\ \hline \end{array}$

Good morning!

What is the residue modulo 13 of the sum of the modulo 13 inverses of the first 12 positive integers?
Express your answer as an integer from 0 to 12 , inclusive.

$\begin{array}{|rcll|} \hline 1\cdot { \color{red}1} &\equiv& 1 \pmod{13} \\ 2\cdot 2^{-1} \equiv \pmod{13} \equiv 2\cdot { \color{red}2^{11}} \pmod{13} &\equiv& 1 \pmod{13} \\ 3\cdot 3^{-1} \equiv \pmod{13} \equiv 3\cdot { \color{red}3^{11}} \pmod{13} &\equiv& 1 \pmod{13} \\ 4\cdot 4^{-1} \equiv \pmod{13} \equiv 4\cdot { \color{red}4^{11}} \pmod{13} &\equiv& 1 \pmod{13} \\ 5\cdot 5^{-1} \equiv \pmod{13} \equiv 5\cdot { \color{red}5^{11}} \pmod{13} &\equiv& 1 \pmod{13} \\ 6\cdot 6^{-1} \equiv \pmod{13} \equiv 6\cdot { \color{red}6^{11}} \pmod{13} &\equiv& 1 \pmod{13} \\ 7\cdot 7^{-1} \equiv \pmod{13} \equiv 7\cdot { \color{red}7^{11}} \pmod{13} &\equiv& 1 \pmod{13} \\ 8\cdot 8^{-1} \equiv \pmod{13} \equiv 8\cdot { \color{red}8^{11}} \pmod{13} &\equiv& 1 \pmod{13} \\ 9\cdot 9^{-1} \equiv \pmod{13} \equiv 9\cdot { \color{red}9^{11}} \pmod{13} &\equiv& 1 \pmod{13} \\ 10\cdot 10^{-1} \equiv \pmod{13} \equiv 10\cdot { \color{red}10^{11}} \pmod{13} &\equiv& 1 \pmod{13} \\ 11\cdot 11^{-1} \equiv \pmod{13} \equiv 11\cdot { \color{red}11^{11}} \pmod{13} &\equiv& 1 \pmod{13} \\ 12\cdot 12^{-1} \equiv \pmod{13} \equiv 12\cdot { \color{red}12^{11}} \pmod{13} &\equiv& 1 \pmod{13} \\ \hline \end{array}$

$\begin{array}{|ll|} \hline & \text{sum}_{\text{of the modulo 13 inverses of the first 12 positive integers}} \\ =& 1^{11}+2^{11}+3^{11}+4^{11}+5^{11}+6^{11}+7^{11}+8^{11}+9^{11}+10^{11}+11^{11}+12^{11} \pmod{13} \\ =& 1+7+9+10+8+11+2+5+3+4+6+12 \pmod{13} \\ =& 1+2+3+4+5+6+7+8+9+10+11+12 \pmod{13} \\ =& \dfrac{1+12}{2}\cdot 12 \pmod{13} \\ =& 13 \cdot 6 \pmod{13} \\ \mathbf{=}& \mathbf{0 \pmod{13}} \\ \hline \end{array}$

Let $\large{p(x) = 2x^2 + 7x + c}$,
where $c$ is not equal to $0$.
If $\large{r_1}$ and $\large{r_2}$ are the roots of $\large{p(x)}$,

then find the value of $\large{\dfrac{1}{r_1}} + \large{\dfrac{1}{r_2}}$in terms of $\large{c}$.

$\begin{array}{|rcll|} \hline p\left(\dfrac{1}{x}\right) = 2\left(\dfrac{1}{x}\right)^2 + 7\dfrac{1}{x} + c &=& 0\\\\ \dfrac{2}{x^2} + \dfrac{7}{x} + c &=& 0 \quad | \quad \cdot x^2 \\ 2 + 7x + cx^2 &=& 0 \\ cx^2+7x+2 &=& 0 \\\\ x &=& \dfrac{-7\pm\sqrt{7^2-4\cdot c\cdot 2}}{2c} \\ x &=& \dfrac{-7\pm\sqrt{49-4c}}{2c} \\ \dfrac{1}{r_1} + \dfrac{1}{r_2} &=& \dfrac{-7+\sqrt{49-4c}}{2c} + \dfrac{-7-\sqrt{49-4c}}{2c} \\\\ &=& \dfrac{-7+\sqrt{49-4c}-7-\sqrt{49-4c}}{2c} \\\\ &=& \dfrac{-14}{2c} \\\\ \mathbf{\dfrac{1}{r_1} + \dfrac{1}{r_2} } &\mathbf{=}& \mathbf{ -\dfrac{7}{c} } \\ \hline \end{array}$

If

$\large{f(x)=\dfrac{a}{x+2}}$,

solve for the value of a so that

$\large{f(0)=f^{-1}(3a)}$.

$\begin{array}{|rcll|} \hline f\left(~ f^{-1}(x) ~\right) &=& x \quad & | \quad x = 3a \\ f\left(~ f^{-1}(3a) ~\right) &=& 3a \quad & | \quad f^{-1}(3a) = f(0) \\ f\left(~ f(0) ~\right) &=& 3a \quad & | \quad f(0) = \dfrac{a}{0+2}=\dfrac{a}{2} \\ f\left(~ \dfrac{a}{2} ~\right) &=& 3a \quad & | \quad f\left(\dfrac{a}{2} \right) = \dfrac{a}{\dfrac{a}{2}+2}=\dfrac{2a}{a+4} \\ \dfrac{2a}{a+4} &=& 3a \\ \dfrac{2 }{a+4} &=& 3 \\ 2 &=& 3 (a+4) \\ 2 &=& 3a+12 \\ 3a &=& -10 \\ \mathbf{a} &\mathbf{=}& \mathbf{-\dfrac{10}{3}} \\ \hline \end{array}$

Perhaps these graphs will help (note, I've rearranged your equality to create a function f that is zero when the equality is true):

3. 

As shown in the diagram Line AD, Line BE  and Line CF are concurrent. We know that CD=CE=BF=4 and BD=AF=6. What is AE?

As shown in the diagram Line AD, Line BE  and Line CF are concurrent.

We know that CD=CE=BF=4 and BD=AF=6. 

What is AE?

Ceva's Theorem:

$\begin{array}{|rcll|} \hline \dfrac{AF}{BF}\cdot\dfrac{BD}{CD}\cdot\dfrac{CE}{AE} &=& 1 \\ \\ \dfrac{6}{4}\cdot\dfrac{6}{4}\cdot\dfrac{4}{AE} &=& 1 \\ \\ \dfrac{36}{4AE} &=& 1 \\ \\ AE&=& \dfrac{36}{4} \\ \\ \mathbf{AE}&\mathbf{=}& \mathbf{9} \\ \hline \end{array}$

There seems to be 2 different questions here.

I will answer the first one.

Let  a  and  b  be real numbers. The complex number    4 - 5i     is a root of the quadratic

$z^2 + (a + 8i) z + (-39 + bi) = 0$.

I am told that one solution is z=4-5i

so

$(4-5i)^2 + (a + 8i) (4-5i) + (-39 + bi) = 0\\ \text{expand and simplify and we get}\\ (4a-8)+(b-5a-8)i=0\\ so\\ 4a-8=0\\ a=2\\ b-5a-8=0\\ b=18\\ \text{so the equation becomes}\\ z^2 + (2 + 8i) z+ (-39 + 18i) = 0\\ $

Now I will use the quadratic formula to solve this.

$z^2 + (2 + 8i) z+ (-39 + 18i) = 0\\ z = {-(2 + 8i) \pm \sqrt{\triangle} \over 2}\\ (-1-4i)\pm\frac{\sqrt{\triangle}}{2}=4-5i \qquad \text{I'm not sure if it is + or - so i will keep it together}\\ \pm\frac{\sqrt{\triangle}}{2}=5-i\\ \text{So the solutions are}\\ z=-1-4i\pm (5-i)\\ z=-1-4i+ (5-i) \qquad z=-1-4i- (5-i)\\ z=4-5i \qquad \qquad \quad \qquad z=-6-3i\\~\\ \text{So the other root is } -6-3i$