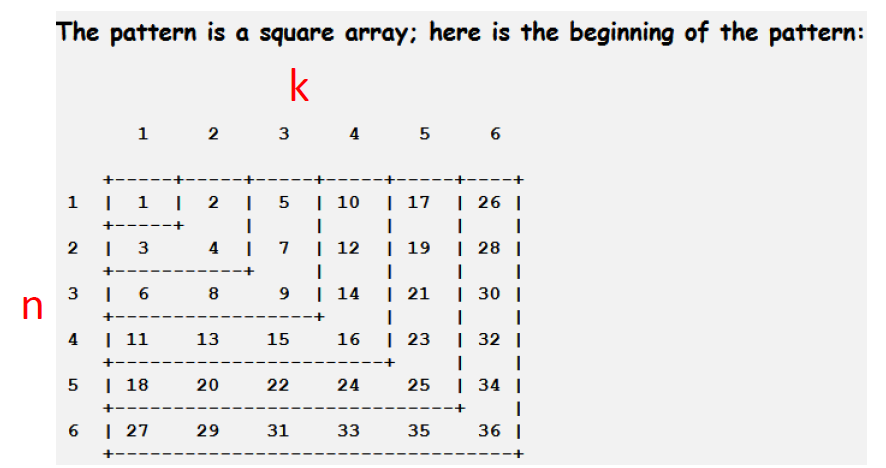
the positive integers are arranged in the pattern illustrated below if this pattern continues indefinitely, what is the number immediately above 39863?
1 2 5 10 17 26
3 4 7 12 19 28
6 8 9 14 21 30
11 13 15 16 23 32
18 20 22 24 25 34
27 29 31 33 35 36
Let row = n
Let column = k
Formula:
\(\begin{array}{|rcll|} \hline T(n,k) &=& (k-1)^2+2n-1 \qquad & n\le k \\ T(n,k)&=&(n-1)^2+2k \qquad & n>k \\ \hline \end{array}\)
Source: http://oeis.org/search?q=a185725&sort=&language=english
1. \(\begin{array}{|rcll|} \hline \sqrt{39863} &=& 199.657\ldots \\ n_{min} &=& 199 \\ n_{max} &=& 200 \\ \hline \end{array}\)
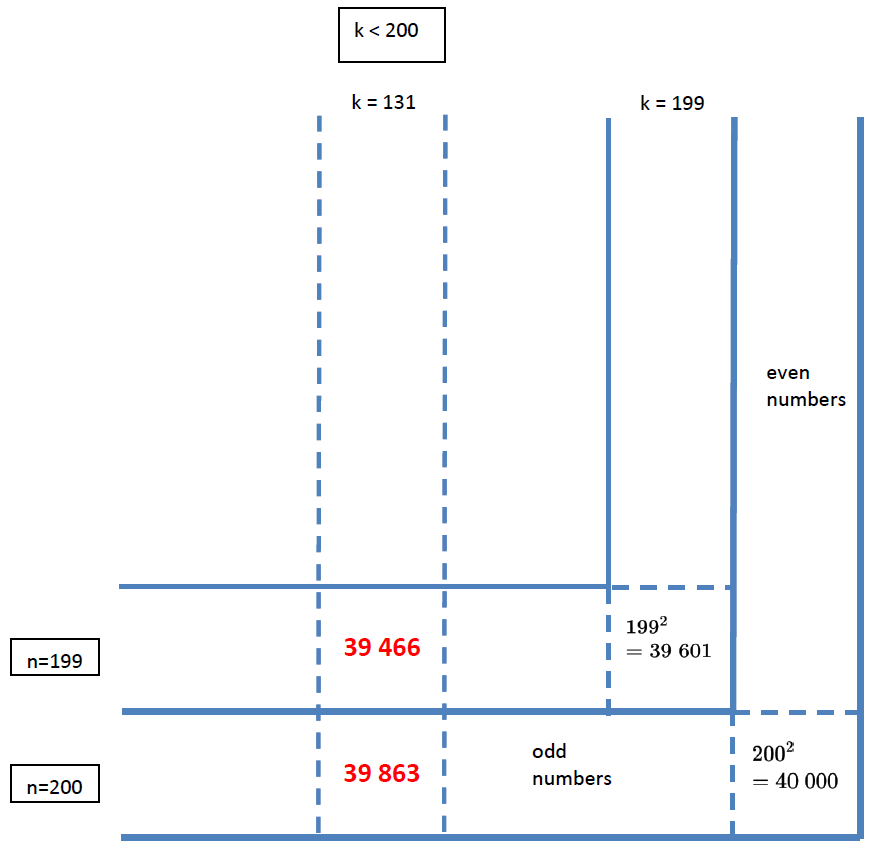
\(\begin{array}{|rcll|} \hline T(200,k) &=& (200-1)^2+2k \qquad & n>k \\ 39863 &=& 199^2+2k \\ 2k &=& 39863 - 199^2 \\ 2k &=& 262 \\ \mathbf{k}& \mathbf{=}& \mathbf{131} \\ \hline \end{array} \)
The number immediately above:
\(\begin{array}{|rcll|} \hline T(199,131) &=& (199-1)^2+2\cdot 131 \qquad & n>k \\ T(199,131) &=& 198^2+2\cdot 131 \\ \mathbf{T(199,131)} & \mathbf{=}& \mathbf{39466} \\ \hline \end{array}\)
![]()