All Answers 356736 Answers

We have these two equations

1 ≤ 4 - 3y                   and     4 - 3y < 10                   rearrange both as

3y ≤ 4 - 1                              -6 < 3y

3y ≤ 3                                                                         divide both sides by 3

y ≤ 1                                    -2 < y

So....the interval that solves this is (-2, 1 ]

So...the y's that DON'T solve this are

(-inf, -2] and (1, infinity )

If we connect the centers of the circles, this will form an equilateral triangle

The two sides of this triangle meeting at any vertex will pass through the points of tangency where one circle meets the other two......these two tangent points form the endpoints of one side of the shaded region

Since the vertex angle of the triangle = 60°.....then the arc formed by one side of the shaded region = 1/6 the circumference of the circle = 6 units

So....the perimeter of the shaded region is 3 times this = 18  units

This is a binomial probability

P(2 tails)  = C(7,2) * (1/2)^2 * (1/2)^5  =  C(7, 2) (1/2)^7  =  21 / 128

Thanks, asdf...!!!!

Here's a more general solution :

Angle EBP = Angle FDP

And angle BPE = angle DPF

So...by AA congruency.....triangle EBP is similar to triangle FDP

Note that EB is   2/3  of AB  = 2/3 of CD

And FD  is 1/2 of CD

So....   EB /FD =  (2/3)CD / (1/2)CD  =  4/3

So....EB is (4/3) FD

So....the height of EBP must be (4/3) the height of FDP

So.....there are 7 equal  parts of AD.....and the height of EBP  must be 4 of these

So.....height of EBP = (4/7)AD

So.....the area of EBP  =  (1/2)*(2/3)AB * (4/7)AD  = (1/3)(4/7)(AB)(AD)  = (4/21)(AB)(AD)  = 

(4/21) area of ABCD

she plays in 5+5-1 games, or 9 games.

there are 10c2 games played total or 45

so the answer is 9/45 or 1/5.

HOPE THIS HELPED!

There are 10 players in all.....Anita is ONE of them..... she must play 9 other players

  We have already shown there are a total of 45 games          Anita plays  9/45 games = 1/5 of the games

good job cphill!

i suppose you could try plugging in 1, 2, 3, 4 and seeing if there is a pattern

EDIT: nevermind i read want you wanted

Let's suppose that a line goes through the points  (2, 3)  and (4 , 6)

We can find the slope of the line as   [ 6 - 3 ] / [ 4 - 2]  = 3 / 2

Using this  and the either of the points....we have

y = (slope) ( x - x coordinate of point) + y coordinate of point

y = (3/2) ( x - 2) + 3            distribute the 3/2 over the terms in parentheses

y = (3/2)x - 3  + 3

y = (3/2)x 

And that's the equation of the line

Not a particularly "geometric" solution....but see the following image

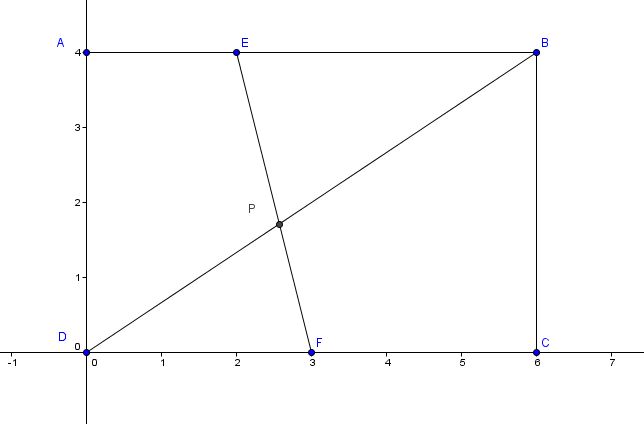
Let A  = (0,4)  B = (6, 4)   C = (6,0)   D = ( 0, 0) E = (2, 4) F = (3,0)

The segment connecting  BD has the slope 2/3

And its equation is y = 2/3x

The segment connecting EF has a slope of  [ 4 - 0 ] / [ 2 - 3 ] =  -4

So....its equation is  y = -4(x - 3)  ⇒  y = -4x + 12

The x coordinate for P is

(2/3)x = -4x + 12

(2/3)x + 4x  = 12

(14/3)x = 12

x = 36/14 = 18/7

And its y coordinate is   y = (2/3)(18 7)  =  36/21  =  12/7   

So.....the base of EBP = 4

And its height is  4 - 12/7 =  16/7

So...its area =  (1/2)(4)(16/7) = 32/7

And the area of the rectangle = 6 * 4 = 24

So....the fractional area of   EBP to the area of the rectangle is

(32/7) /  24  =    32 / 168   =   4 / 21

Usually you'll try to pick two points off of the graph of the line that are clearly defined.

Having done that it's simple to compute the slope and then use point slope form to find the equation of the line.

16 - 4 * x  >10   Subtract 16 from both sides of the equation

-4 x > -6            Multiply both sides by -1    NOTE:     >   reverses when you do this !

4x < 6              Divide by 4

x  <  6/4 

x < 1  1/2        Only ONE positive integer will satisfy this   x = 1

i have posted the question cphill you can solve it if you want :P

OK......post away, asdf......!!!!!

that was what the answer was though... 420

i am going to post my own question; i can probably solve it on my own but i will post it anyway

LOLOLOLOLOLOLOLOL

LOL!!!!!

yep!!

OK...by unanimous consensus.....2 / 9   it is.....!!!!!

As in your other question....the girls play 10 games against each other

And the boys play the same number

Each boy (or girl)  plays the opposite counterpart  5 * 5  = 25 times

So......the number of total games =  10 + 10 + 25  =  45

So....the fractional number of boy-boy games is   10 / 45   =  2 / 9

We found from Chris' previous answer that girl vs girl  (or boy vs boy) is 10 games

Total games would be   10C2 = 45

10/45 = 2/9