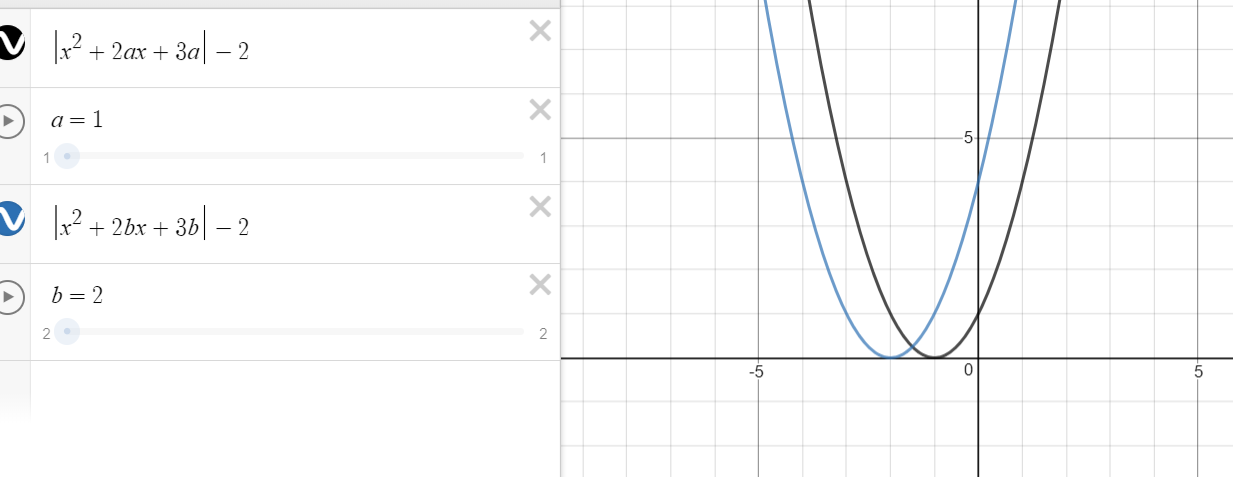
+118703 Determine all real numbers a such that the inequality |x2+2ax+3a|≤2 has exactly one solution in x.
From the graph I have draw in Desmos I can see that this has exaclty 2 solutions. a=2 and a=1
https://www.desmos.com/calculator/fewruikgqj
|x2+2ax+3a|≤2|x2+2ax+3a|−2≤0
Take a look at the graph and see if you can work out what it is showing you.
Now I will talk it through algebraically:
Now y=x2+2ax+3a is a concave up parabola. When it is put in absolute signs the bit in the middle, that was under the x axis is reflected in the x axis. So effectively this means that the bit between the roots becomes a concave down parabola.
When this is dropped by 2 units there will be either 2 or 4 roots. So x2+2ax+3a must be positive (because there can only be one root.)
|x2+2ax+3a|=2x2+2ax+3a>0sox2+2ax+3a=2x2+2ax+3a−2=0x2+2ax+(3a−2)=0I only want one solution so the discriminant must be 0(2a)2−4∗1∗(3a−2)=04a2−12a+8=0a=12±√144−1288a=12±√168a=12±48a=168or88a=2or1
Hence
Whena=1|x2+2x+3|≤2is the same as x2+2x+3≤2And it has only one solution x=−1
and
Whena=2|x2+4x+6|≤2is the same as x2+4x+6≤2And it has only one solution x=−2
