All Answers 357330 Answers

Awesome thank you !

I see that now it would be A ! Thank you so much

sinx      multiply by 2  = 2 sinx

2 sinx      add   3    =   2 sin x   + 3       the amplitude changes from 1 to 2  and it is shifted up 3 units  Answer   A

sin x        stetch it vertically by 2    =    2 sin x     then add 3      2 sin x   + 3       (both questions same function)

 fill 5 cup......fill 3 cup from 5 cup leaves 2 cups in the larger ....pour out 3 cup and put the 2 cup in it

                fill 5 cup again and pour 1 cup in to 3 cup (thus filling the 3 cup container).....now there is 4 cups in 5 cup container.

Looks OK !

https://web2.0calc.com/questions/select-all-that-are-true

Fill the 5 cup container full, (5,0)

Fill the 3 cup container full using the 5 cup container, which afterward contains 2 cups, (2,3)

Pour out the 3 cup container and fill it with the 2 cups remaining in the 5 cup container, (0,2)

Fill the 5 cup container, (5,2)

Top off the 3 cup container using the 5 cup container.  This takes 1 cup from the 5 into the 3, (4,3)

You now have 4 cups in the 5 cup container.

Yah, flipping back and forth betwen the screenshot and the Forum, I sometimes get the numbers incorrect..... 

Here is pic:

i got it thanks 

it should end up looking like this http://prntscr.com/mbnq1b   ?

with the editing

Sin wave     sin (x) is parent wave

Period = 24 hours     2pi/24 = pi/12        now sin (pi/12 *x)

Amplitude = (8.3-0.4) / 2 = 3.95          now   3.95 sin ( pi/12 *x)

Midline shifted UP 4.35                  now     3.95 sin (pi/12 *x) + 4.35

thank you very much 

Correct.

f₁(x)=cos(x)

f₂(x)= - cos(x) - 2

solve for x 4/(x-1)-1/(4+x)+x/3=4

Reflect by making  cosx       - cos x       shift down by subtracting 2       so  :     - cos x    -  2

No....sorry.     3 is the amplitude of the modulated wave.    Normal midline for a cos wave is y = 0  .  This wave is SHIFTED DOWNWARD by 2.5 so the midline woudl be at  y = -2.5 .

1  false    look at the lowest point   7.5 s    4 ft    it does not get back to lowest point until 17.5 s     so one rev = 10 seconds

2 true      Highest point  64 ft    lowest point 4 ft   means DIAMETER is 60 ft     radius is 30 ft

3 true

4 false     Lowest point is 4 ft.....at t= 0 s  the ferris wheel is at 34 ft high.

1,376.06 K - 273.15 = 1102,91°C

Of all numbers between 1 and 15! (factorial),

how many of them are BOTH perfect squares and perfect cubes for the same number(such as 64)?

lcm(2,3) = 6  (least common multiple)

So the numbers that are going to be perfect squares and perfect cubes are precisely the 6th powers of the integers:
$\begin{array}{rcll} 1^6 &=& 1 \\ 2^6 &=& 64 \\ 3^6 &=& 729 \\ 4^6 &=& 4096 \\ 5^6 &=& 15625 \\ ... \\ n^6 &<& 15! \\ \end{array}$

So n are the numbers between 1 and 15! (factorial)

$\begin{array}{|rcll|} \hline n^6 &<& 15! \\ n &<& \sqrt[6]{15!} \\ n &<& \sqrt[6]{1~307~674~368~000} \\ n &<& 104.57228596314317\ldots \\ \mathbf{n} & \mathbf{=} & \mathbf{104}\\ \hline \end{array}$

104 of them are BOTH perfect  squares and perfect cubes.

In rhombus ABCD, points E,F,G, and H are the midpoints of lines AB,BC,CD, and DA respectively.
Quadrilateral EFGH has area 14 and perimeter 16.
Find the side length for rhombus ABCD.

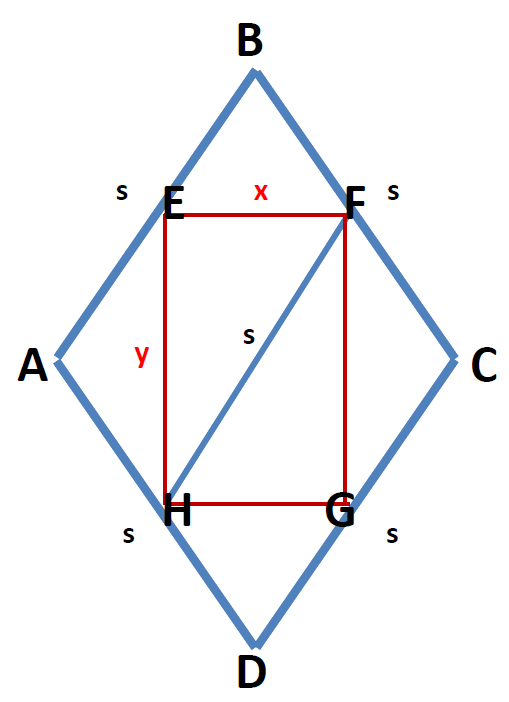
$\text{Let $EF$ = x } \\ \text{Let $EH$ = y } \\ \text{The side length for rhombus $=AB=BC=CD=DA=HF$ = s }$

$\begin{array}{|lrcll|} \hline 1. & xy&=&14 \\ & y&=& \dfrac{14}{x} \\\\ 2. & 2(x+y)&=& 16 \\ & \mathbf{x+y} & \mathbf{=} & \mathbf{8} \quad & | \quad y= \dfrac{14}{x}\\ & x+\dfrac{14}{x} &=& 8 \quad & | \quad \cdot x \\ & x^2+ 14 &=& 8x \\ & x^2-8x+ 14 &=& 0 \\ & x &=& \dfrac{8\pm \sqrt{64-4\cdot 14} }{2} \\ & x &=& \dfrac{8\pm \sqrt{4(16-14)} }{2} \\ & x &=& \dfrac{8\pm 2\sqrt{ 16-14 } }{2} \\ & x &=& \dfrac{8\pm 2\sqrt{ 2 } }{2} \\ & x & = & 4\pm \sqrt{ 2 } \\ & \mathbf{x} & \mathbf{=} & \mathbf{4- \sqrt{ 2 }} \\\\ & \mathbf{x+y} & \mathbf{=} & \mathbf{8} \quad & | \quad x=4-\sqrt{ 2 } \\ & 4-\sqrt{ 2 }+y &=& 8 \\ & y &=& 8-(4-\sqrt{ 2 }) \\ & y &=& 8-4+\sqrt{ 2 }) \\ & \mathbf{y} & \mathbf{=} & \mathbf{4+ \sqrt{ 2 }} \\ \hline \end{array}$

$\mathbf{s =\ ?}$

$\begin{array}{|rcll|} \hline s^2 &=& x^2+y^2 \quad & | \quad \mathbf{x= 4- \sqrt{ 2 }},~ \mathbf{y= 4+ \sqrt{ 2 }} \\ s^2 &=& (4-\sqrt{2})^2+(4+\sqrt{2})^2 \\ s^2 &=& 16-8\sqrt{2} + 2 + 16 +8\sqrt{2} + 2 \\ s^2 &=& 16 + 2 + 16 + 2 \\ s^2 &=& 36 \\ \mathbf{s} & \mathbf{=} & \mathbf{6} \\ \hline \end{array}$

The side length for rhombus ABCD is 6

Hello CDorrell,

I can see you have already edited this question twice (after it is anwered) and and each time you have changed it to completely different question.

This is extremely rude. 

Questions should nrarely be editied and they NEVER should be entirley changed. The facility is intended only for when people make minor posting errors and even then they shoud make it clear what changes they have made.

Please do not edit your questions, or answers, in any way that can be considered rude or inconsiderate, in the future.

At 5:00 P.M. on a Friday, Hal got locked in the vault. he was there for 5040 minutes before it opened. Om what day did it open?

5040/60 = 84 hours

84/24 = 3.5 days

5pm Frid+half a day =  5am Saturday

5am sat + 3 days = 5am Tuesday

Open on Tuesday   (5am)