All Answers 356369 Answers

the numbers I lised are the number of white flower seeds in each group

My answer is correct now.   :)

Thanks guest for the little line of code to work it out.

What language is it coding for?

I must learn some coding one day, it is on my 'to do' list LOL

Also thanks guest for recognising that all these numbers are multiples of 1125

I can see it is logical that this would happen.      :)

Yes sorry.

It has just been pointed out to me that I mad a careless error that trivialized the answer. (My wrong answer I mean.)

It should not have been 8, it should have been 8d in the working.

I'll fix that and then I will think about it    

please help me

thank you

i'm assuming you mean -7x

add the equations

-3x = 21

x = -7

plug in x

-28-8y=20

8y = -48

y = -6

I will take a crack at this one!

I think what they want you to do is to solve the following equations:

11n  +  8m = 96...............(1)

11n  +  8m = 97...............(2)

11n  +  8m = 69...............(3)

Each of the above equations has an infinite number of solutions. Example: The first equation can be solved using n = 8 and m = 1 and thereafter, any multiple of n such as n = 16 and m = -10 (in the sense that you will pay: 16 x 11 confusions=176 - 96 = 80 / 8 confusions =10 that you will get back, and so on....).

The above method applies to all 3 equations above. 

I'm assuming that the 4th one is  y  = (1/4)x - 2

If the first one is  y = 3x^3......then this is non-linear

All the rest ARE linear

[ The third one is a horizontal line at y = 15.3  ]

First one....see the image below :

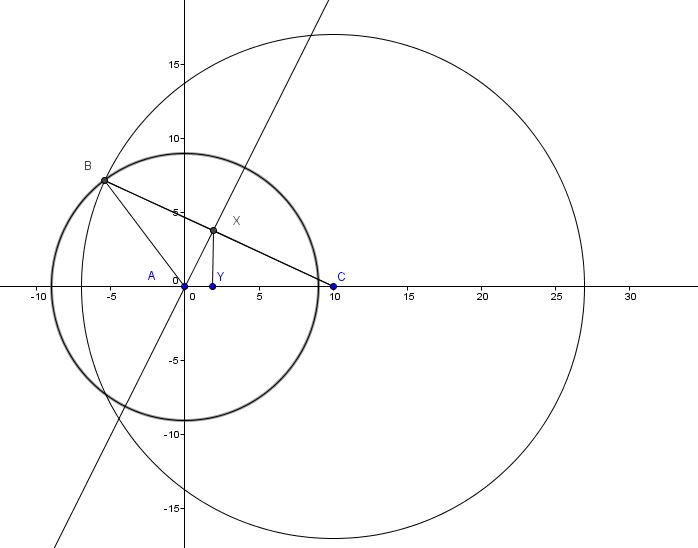
Let A = (0,0)    

Let C = (10,0)

And we can find B, thusly

Construct a circle with radius 9 centered at the origin

The equation of this circle will be  x^2 + y^2 = 81      (1)

And construct a circle wilth radius 17 centered at (10, 0)

The equation of this circle will be  (x - 10)^2 + y^2 = 289  (2)

We can find the coordinates for point B, thusly :

Subtract  (1) from (2)  and we have that

(x-10)^2 - x^2  = 208    simplify

x^2 - 20x + 100 - x^2  = 208

-20x = 108

x = -108/20  = -5.4 =   x coordinate of B

And taking the positive value for y, we have that

(-5.4)^2 + y^2 = 81

y^2 = 81 - 29.16

y = 7.2  =  y coordinate of B

So....B =  (-5.4, 7.2)

And  AX is the bisector of angle A

So....we have the following relationship

AC/AB  = XC /XB

10/9  = XC / XB

Then BC has 19 equal parts and XC is 10 of them.....so  XC = (10/19)*17 = 170/19

So....using a similar triangle idea.....

Distance from B to the x axis / BC  =  XY / XC

7.2 / 17  = XY / (170/19)

(170/19) * 7.2 /17  = XY  =  (170/17)(7.2 / 19) = 10 * 7.2 / 19    =   72 / 19

I'm pretty sure it's the fourth one because it's none of the first three, but you need to use parentheses to identify what goes with what. Is it one-fourth x or is it 1 over 4x, and so on.  You could verify which one it is by actually plotting a few points on a graph.   

.

However, it was indeed correct! Thank you for your help

What is the value of x in the diagram above?

Hello?

3.) What is the least positive integer with exactly 10 factors?

This is given by  :

(2)^4 * 3^1  =   48

2.) How many positive three-digit integers are there in which the sum of its three digits is odd?

We have the following possibilities :

2 integers are even and 1 is odd  or    all three  are odd

First case

(odd)(even)(even)  = (5)(5)(5)  = 125

(even)(odd)(even)  = (4)(5)(5) = 100

(even)(even)(odd) = (4)(5)(5) = 100  

Total  = 325

Second case

(odd)(odd)(odd) = (5) (5) (5)  = 125

So...the total is  325 + 125  =  450

(Which is what we might expect...since there are 900 3-digit numbers....and half of them should have odd sums of their integers)

I've actually never seen a problem like this !!!

I just  used some reasoning   (and hope that we're correct).....LOL!!!!

1.) In the land of Noom, all nouns are 4-letter words with consonants at the beginning and end and a repeated vowel (a, e, i, o, or u) in the middle. How many such words are possible?

We have  21 ways of choosing the first consonant....5 ways of choosing a repeated vowel and (assuming that consonants can also be repeated), 21 ways of choosing the last consonant

So   21 * 5 * 21  =  2205 "nouns"

Thank you for your explanation Cphill you always explain everything so well! To where I can understand it .Thank you for your help! Is this usually how you would always solve problems like this?

19862    28864    96403    88695    87816  

Note in the first group.....the digits 1 and 2  must be the   white flowers planted in this group  = 2

In the second group.....the digits  2 and 4  must be the  white flowers planted in this group = 2

In the next group....the digits 3 and 4  must be the  white flowers planted = 2

In the 4th group....none were planted since the digits 1,2,3,4 don't appear

In the last group....the digit 1 appears...so....1 white flower was planted in  this group

So

2 + 2 + 2 + 0 + 1  =  7

You'll need the input resistance of the TV

\(\text{The center of the original circle is }(0,0)\\ \text{The center of the reflected circle is }(8,2) \text{ (can you see why?)}\\ \text{The radius is unchanged. The equation of the new circle is }\\ (x-8)^2 + (y-2)^2 = 25\\ x^2 - 16x + 64 + y^2 - 4y + 4 = 25\\ x^2 +y^2 -16x-4y+43=0\\ a=1,~b=-16,~c=-4,~d=43\)

May I ask why you only took the values of the first numbers?

A = 2in x 3in = 6 in²