Second one.....see the following image....
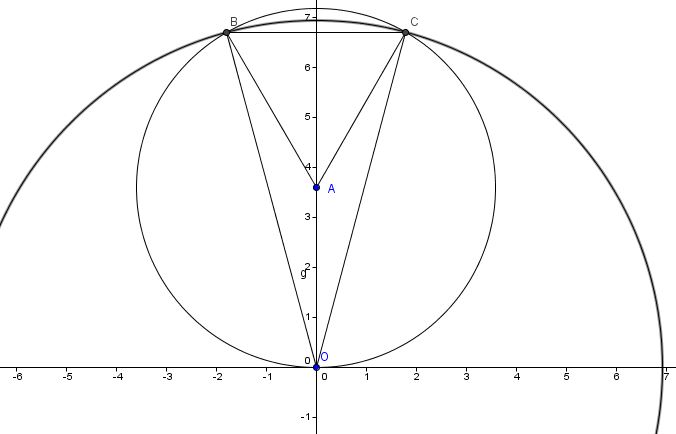
Let O = (0,0)
Since the area of circle O = 48pi....then the radius = √48 units
So...the equation of the circle is x^2 + y^2 = 48
Since ABC is equilateral....then angle BAC = 60°
Then the excluded angle to BAC = 300°
So, by symmetry, angle AOC = 150°
And since A is the circumcenter of triangle BOC, then AO = AC = the side of equilateral triangle ABC = s
And we can find s^2 using the Law of Cosines, thusly :
OC^2 = 2s^2 - 2s^2 * ( cos 150)
48 = 2s^2 + 2s^2* (√3/2)
48 = 2s^2 + s^2√3
48 = (2 + √3)s^2
48 / [ 2 + √3 ) = s^2 = 48 [ 2 - √3] = 96 - 48√3
So....the area of equilateral triangle ABC =
(1/2) s^2 sin (BAC) =
(1/2)s^2 sin(60°) =
(√3) [ 96 - 48√3 ] / 4 =
(√3) [ 24 - 12√3] =
24√3 - 36 units^2


