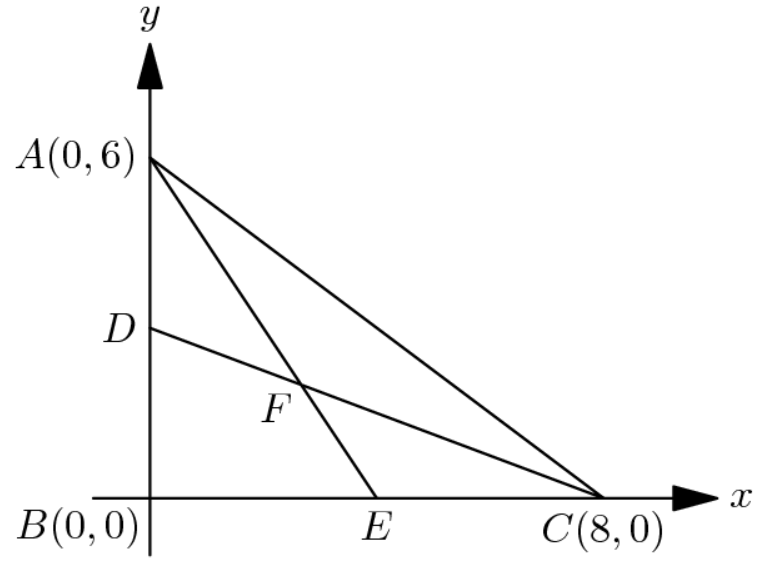
In the diagram, D and E are the midpoints AB of and BC respectively.
Determine the area of quadrilateral DBEF
Centroid of a Triangle: The point where the three medians of the triangle intersect.
So F is the centroid of the triangle ABC.
\(\begin{array}{|rcll|} \hline \vec{F} &=& \frac13 (\vec{A}+\vec{B}+\vec{C}) \\ \vec{F} &=& \frac13 \Big( \binom {0}{6}+\binom {0}{0}+\binom {8}{0} \Big) \\ \vec{F} &=& \frac13 \dbinom {8}{6} \\ \vec{F} &=& \dbinom {\frac{8}{3}}{2} \\ \hline \end{array} \)
\(\begin{array}{lcll} \text{Let } \vec{D} = \dbinom {0}{3} \\ \text{Let } \vec{E} = \dbinom {4}{0} \\ \text{Let } \vec{F} = \dbinom {\frac{8}{3}}{2} \\ \end{array}\)
\(\begin{array}{|r|r|r|r|r|} \hline \text{Point} & x & y & \\ \hline B & 0 & 0 &\\ & & & 0\cdot 0 - 4\cdot 0 & = 0 \\ E & 4 & 0 & \\ & & & 4\cdot 2 - \frac{8}{3}\cdot 0 & = 8 \\ F & \frac{8}{3} & 2 &\\ & & & \frac{8}{3}\cdot 3 - 0 \cdot 2 & = 8 \\ D & 0 & 3 &\\ & & & 0\cdot 0 - 0\cdot 3 & = 0 \\ B & 0 & 0 &\\ \hline & & & & \text{sum} = 16 \\ & & & & \text{area of quadrilateral DBEF } = \dfrac{\text{sum}}{2} = \dfrac{\text{16}}{2} = \mathbf{8} \\ \hline \end{array}\)
