All Answers 357330 Answers

Thanks, Melody!!!!

We still arrived at the same station.....that's encouraging  !!!!

Thanks CPhill!

A LOT more legible than my answer !  LOL.....

If you are asked to factorize it, that is a good start....

((1/2x)^3 - 2^3 )        can you do it now?    

                        x^4  + 2x^3  + 5x^2   + 12x  + 29

x^2 - 2x - 1   [   x^6  +  0x^5  + 0x^4 + 0x^3 + 0x^2 + ax + b ]

                        x^6   -  2x^5   - x^4               

                      ________________________

                                 2x^5    + x^4  + 0x^3

                                 2x^5   -  4x^4 -  2x^3

                               _______________________

                                            5x^4 + 2x^3  + 0x^2

                                            5x^4 -10x^3  - 5x^2

                                           ___________________

                                                     12x^3 + 5x^2 + ax

                                                      12x^3 -24x^2 -12x

                                                    __________________________

                                                                 29x^2 + ( a + 12)x + b

                                                                 29x^2  -    58x      -29

                                                               ____________________________

                                                                              (a + 12 + 58)x + (b + 29)

(a + 70)x  + (b + 29)  =  0

ax + 70x + b + 29  =  0

ax + b   =   -70x - 29

So

a + b     =  -70 + (-29)     =  -99

Here is my scrawled answer..... basically I did the long division and found what values of A and B produce a zero remainder....

a+b = -99

Ohh!! so in any difference of cubes, it must be solved in that form first?

Here is something that may clue you in......

Factoring a Difference of Cubes:

a3 – b3 = (a – b)(a2 + ab + b2)

Melody: These are the numbers I found:
n=1;a= 7*sqrt(-n^2 + 22*n -21); b=n+39;printa,  b,n;n++;if(n<30, goto1,0) 

n = 1 , 2, 3, 17, 18, 19, 20, 21.

Find the number of integers n that satisfy    $7 \sqrt{-n^2 + 22n - 21} \le n + 39.$

Mmm

firstly:

$-n^2+22n-21\ge0\\ n^2-22n+21\le0\\ (n-21)(n-1)\le0\\ 1\le n\le 21$

now

$7 \sqrt{-n^2 + 22n - 21} \le n + 39\\ 49(-n^2 + 22n - 21) \le n^2+78n + 1521\\ -50n^2 +49*22n-78n - 49*21-1521 \le 0\\ -50n^2 +1000n - 2550 \le 0\\ 50n^2 -1000n + 2550 \ge 0\\ n^2 -20n + 51 \ge 0\\ (n-17)(n-3) \ge 0\\ 0\le n \le 3 \qquad or \qquad n\ge17$

Take the intersection of these restrictions and I get

n can equal    1, 2, 3, 17, 18, 19, 20 or  21

You need ot check this. 

Thank you, Melody !

THANK YOU!!!!!!

Thanks Heureka,

Another great answer from you.    

Thanks guest,

I should have remembered to use that identity. 

Tiggsy used it recnently and I spent a lot of time making full sense of his answer. 

Thanks for reminding me of it again!

ITs basically 1000! divide by (500!)^2

How many times can that expression be divide by seven?

_{"It was actually before you postead I relized it was the first one look t te times on the post "}

I do not understand what you just wrote Nickolas. 

Solve for

$0 \text{ to } 2\pi$

$\sin(3x)+\sin(4x)=0$

$\begin{array}{|lrcll|} \hline & \sin(3x)+\sin(4x) &=& 0 \quad | \quad -\sin(3x) \\ & \sin(4x) &=& -\sin(3x) \quad | \quad -\sin(3x) = \sin(-3x) \\ & \sin(4x) &=& \sin(-3x) \quad | \quad \arcsin() \\\\ (1) & 4x + 2\pi n &=& -3x + 2\pi m \quad | \quad +3x \\ & 7x &=& 2\pi z \\ & \mathbf{x} &\mathbf{=}& \mathbf{\dfrac{2\pi}{7} z } \qquad z \in \mathbb{Z} \\\\ (2) & \sin(4x) &=& \sin(-3x) \quad | \quad \sin(-3x) = \sin(\pi -(-3x) ) \\ & \sin(4x ) &=& \sin(\pi + 3x ) \quad | \quad \arcsin() \\ & 4x +2\pi n &=& \pi+3x + 2\pi m \quad | \quad -3x \\ & x &=& \pi + 2\pi z \\ & \mathbf{x} &\mathbf{=}& \mathbf{ \pi + 2\pi z } \qquad z \in \mathbb{Z} \\ \hline \end{array}$

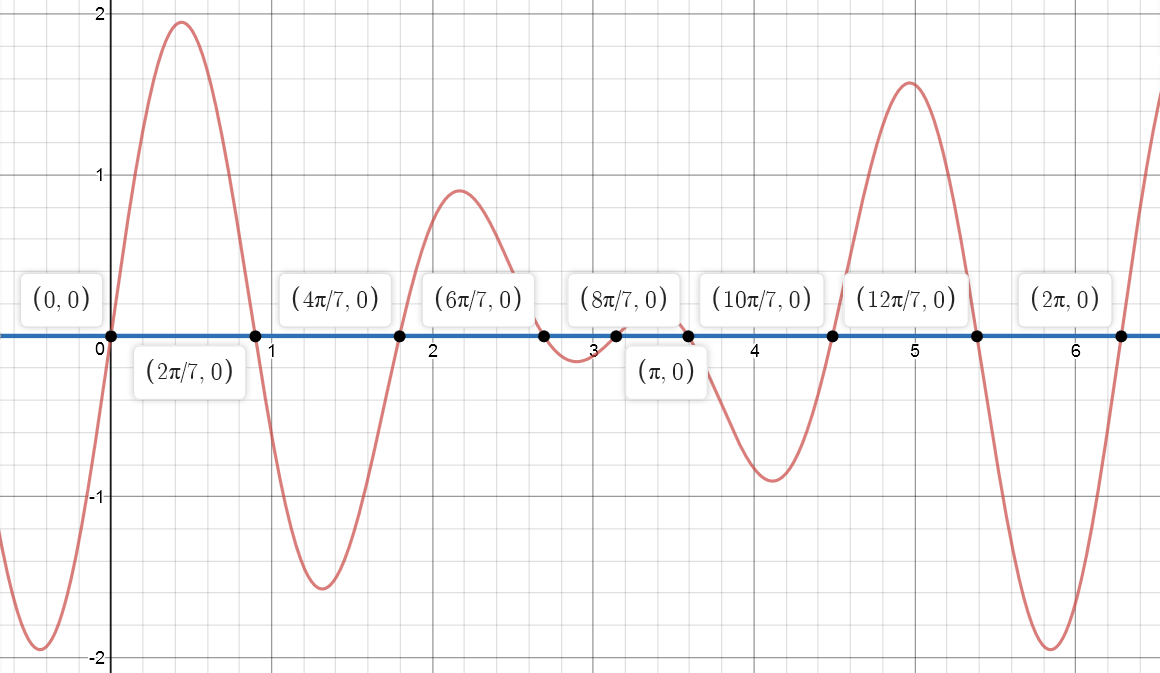
$\begin{array}{|r|r|r|} \hline & 0\le x\le2\pi & 0\le x\le2\pi \\ z & x=\dfrac{2\pi}{7} z & x = \pi + 2\pi z \\ \hline 0 & 0 & \pi \\ 1 & \dfrac{2\pi}{7} & \\ 2 & \dfrac{4\pi}{7} & \\ 3 & \dfrac{6\pi}{7} & \\ 4 & \dfrac{8\pi}{7} & \\ 5 & \dfrac{10\pi}{7} & \\ 6 & \dfrac{12\pi}{7} & \\ 7 & \dfrac{14\pi}{7}=2\pi & \\ \hline \end{array}$

$x = \left\{ 0,\ \dfrac{2\pi}{7},\ \dfrac{4\pi}{7},\ \dfrac{6\pi}{7},\ \pi ,\ \dfrac{8\pi}{7},\ \dfrac{10\pi}{7},\ \dfrac{12\pi}{7},\ 2\pi \right\}$

Trig identity

 $\displaystyle \sin(A)+\sin(B)=2\sin(\frac{A+B}{2})\cos(\frac{A-B}{2})$.

So,

$\displaystyle \sin(3x)+\sin(4x)=2\sin(\frac{7x}{2})\cos(\frac{x}{2})$,

so

$\displaystyle \sin(\frac{7x}{2})=0,\text{ or }\cos(\frac{x}{2})=0$

etc..

Show me how you think the forth one works

left hand side is       (3*4a) - 2       What two things are multipled here.   

One thing is (3*4a)  the other thing is (2)   there is a minus sign between them.    NOT a times sign!

The first one has 12a-6  on the right side.   This is not (one thing) X (another thing.)    So it is not right

the third one is not correct either.  Why??     

Which one is    first thing x second thing =  second thing x first thing              ??

Not so easy.

Here is the graph of y=sin(3x)+sin(4x)

The solutions are the intersections of this graph with y=0    (the x axis)

You can see that there are 9 solutions.    (including x=0 and x=2pi)