All Answers 358181 Answers

Given that  a  and  b  are positive integers where  a > b , I do think it is always true that

a mod (a - b)   =   b mod (a - b)

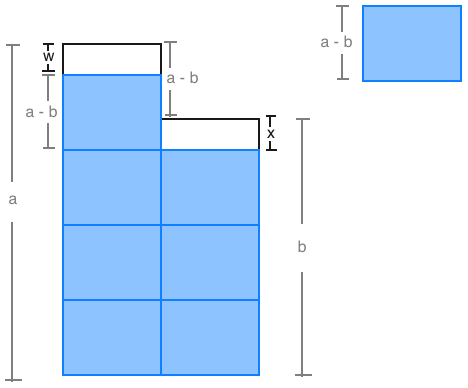
I don't know the best way to explain it, but here is how I convinced myself. In the diagram,

w  is the remainder when  a  is "filled up" with as many blocks of width  a-b  as possible.

x  is the remainder when  b  is "filled up" with as many blocks of width  a-b  as possible.
 

In other words,

w  =  a mod (a - b)

x  =  b mod (a - b)

And we can see that...

w + (a - b)  =  x + (a - b)

w  =  x

Therefore,

a mod (a - b)  =  b mod (a - b)

But I do not think it is always true that if     a mod  x  =  b mod x     then     x  =  a - b

For example,     10 mod 3  =  4 mod 3     but     3  ≠  10 - 4

4cos (50) cos(40) - 4sin(27.5)sin(17.5)

2 [2cos(50) cos(40)  - 2sin (27.5)sin(17.5) ] =

2 [ cos (50 - 40) + cos (50 + 40)  -   [ cos (27.5 - 17.5)  - cos(27.5 + 17.5) ]  ]   =

2 [ cos(10) + cos(90)  - cos(10) +cos(45) ]  =

2cos(90)  +  2cos(45)  =

   0   +  2√2 / 2  =

√2

\($\frac{3}{2\sqrt[3]{5}}$ \)   =     

        3                  [ 5^(2/3) ]

_________         ________   =

2 * (5)^(1/3)         [5^(2/3) ]

3 [ 5^(2/3) ]                  3 *(5^2)^(1/3)              3 ∛25

___________   =        ____________  =       ______

    2 * 5                               10                            10

A = 3   B  = 25    C = 10

And their sum  =   38

18x^2 + 21x - 400

Let r and s be the roots

The sum of the roots , r + s , =  -21/ 8

The product of the roots, rs  =  -400/18  =  -200/9

So

(r + s)^2  = (-21/8)^2

r^2 + 2rs + s^2  =  (441/64)

r^2 + 2(-200/9) + s^2  = 441/64

r^2 + s^2 - 400/9  = 441/64

r^2 + s^2  =  441/64 + 400/9

r^2 + s^2 =  29569 / 576

y^2 - 19y + 7                      (r - 2) (s - 2)  =  rs - 2s - 2r + 4  =  rs -2(r + s) + 4

Using Vieta's Theorem

The sum of the roots , (r + s)  = 19

The product of the roots, rs  = 7

So  

(r - 2) (s - 2)  =  rs - 2(r + s) + 4  =    7 - 2(19) + 4   =    -27

THX, Guest.....careless error  !!

CPhill: Your final answer should read:
[7 + 2sqrt(10)] / 3

x^2 + 6x + 9  = 20                              x^2 + 6x + 9  = 40                              

(x + 3)^2  = 20                                   (x + 3)^2  = 40

x + 3  = √20                                        x + 3 = √40

x = √20 - 3                                          x  = √40 - 3

x = ceiling [ √20 - 3 ]  = 2                    x = floor [ √40 - 3 ]  = 3

As hectictar found....2 and 3 fit the bill....!!!!!

√5 + √2      [ √5 + √2 ]            5 + 2√10 + 2                  7 + 2√10

______      _________ =      _____________ =         _________

√5 - √2       [ √5 +  √2 ]                5    -   2                            3

A + B  + C  +  D  =

7 + 2 + 10 + 3  =

22

CORRECTED

Given that 3x + y = 10 and x + 3y = 14, find 10x^2 + 12xy + 10y^2.

3x + y  = 10      (1)

x + 3y = 14   ⇒  -3x - 9y = -42    (2)     add (1) and (2)

-8y  =  -32    divide through by -8

y = 4

So  using (1)     3(x) + 4  = 10

                         3(x)  = 6

                            x = 2

So     

10x^2 + 12xy + 10y^2    = 

10 (2)^2 + 12 (2)(4) + 10(4)^2  =  

40 + 96 + 160  =

296

I’m confused. Don’t you have to find A+B+C+D?

If (x + y)^2 = 105 and x^2 + y^2 = 65, what is the value of xy?

(x + y)^2  = 105

x^2 + 2xy + y^2  = 105  

(x^2 + y^2)   + 2xy  = 105

(65) + 2xy  = 105    subtract 65 from both sides

2xy =  40              divide both sides by 2

xy =  20

I think: 14 / 17

\(\frac{\sqrt5+\sqrt2}{\sqrt5-\sqrt2}\)

the bottom is sqrt5 - sqrt 2

You just have to multiply both the top and the bottom by sqrt5 + sqrt2    

That fact that the top is the same is just a coincidence. 

Just wrong with the final term, which should be +2cos(45).

That is brilliant Hectictar!   Thanks!  

It is going int the sticky topics. Later I might combine it in one of the other threads but for now it can stand alone and people can be referred to it :)

If 3/20 trees are infested and there are 1200 trees total, then 3/20*1200=180 so there should be around 180 infested trees.

You are very welcome!

:P

Here is my "guess":

9/11  x  (4 1/9 / 4) =37 / 44

Thank you so much!

"For alcohol the formula is 2,4 J/g·°C and for olive oil it is 1,65 J/g·°C. John heats up both substances using a calorimeter, first an unknown amount of alcohol and then, when the calorimeter has cooled completely, the same amount of olive oil. He heats up both liquids from 20 °C to 50 °C. How long does it take to heat up the alcohol when the heating up of the olive oil took 2,5 minutes?"

As follows:

Can you make your LaTeX code display properly?

Here's how:

1) Select the code between the dollar signs

2) On the keyboard, press CTRL+C to copy the text

3) Click the LaTeX button in the editor

4) Delete the the example code

5) On the keyboard, press CTRL+V to paste the text

6) Press the green OK button

Like this:

*edit*

If you do not see the dollar signs in your question, that may be due to the browser you are using.