All Answers 358468 Answers

I would like to see this one answered too.    

That is good.  

It is a good way to do these but a lot of teachers teach what I think is a more complicated method.

Thank you Melody, I think i understand it better now

(you might have just taught me something i would have never thought about using or doing)

8x^2 - 10x - 25

8*-25=-200

So I want 2 numbers that add to -10 and multiply to -200

The bigger one will be negative and the smaller one will be positive (absolute values I mean)

The fairly obvious combination is   -20 and 10

-10x is replaced with -20x+10x

= 8x^2 -20x+10x - 25

Now factorise in pairs

= 4x(2x-5) + 5(2x-5)

= (4x+5)(2x-5)

1st question, 

The point "Q" is 0 horizontally, (x-axis) 

and 3 up vertically (y-axis) so it is (0,3) 

Hence, we write points like: (x,y) 

2nd question,

The slope formula is 

\(y_2-y_1/x_2-x_1\) ( / is divided) so pick any 2 points on the slope and use this formula. 

Let's pick: 

(1,2) , (-1,-2) 

-2-2/-1-1 = -4/-2 = 4/2=2  (slope) 

also it is rise/run look at the change in x and y, x goes 1 to the right, y goes 2 up 

so slope is =2

First question, 

The point-slope form is: 

\(y-y_1=m(x-x_1)\)

Where \(x_1\) and \(y_1\) are the points (In your question the given point passing through the point (7,1)) x_1 is 7, y_1 is 1

m is the slope

so y-1=-4(x-7)

1st choice

Second question: 

Similar answer,

write it in point-slope form,

y-(-1.4) =1.9(x-4.5)

so,

y+1.4=1.9(x-4.5)

Second choice. 

​ Please help

\(\dfrac{\sec^2 \left(\dfrac{4}{x} \right)-1}{\cos \left(\dfrac{6}{x} \right)-\cos \left(\dfrac{2}{x} \right)} \)

\(\begin{array}{|rcll|} \hline && \mathbf{\dfrac{\sec^2 \left(\dfrac{4}{x} \right)-1}{\cos \left(\dfrac{6}{x} \right)-\cos \left(\dfrac{2}{x} \right)}} \\\\ &&\qquad \boxed{\sec^2 \left(\dfrac{4}{x} \right)-1 = \dfrac{\sin^2 \left(\dfrac{4}{x} \right)}{\cos^2 \left(\dfrac{4}{x} \right)} \\~\\= \sin^2 \left(\dfrac{4}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } \\\\ &=& \dfrac{\sin^2 \left(\dfrac{4}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } {\cos \left(\dfrac{6}{x} \right)-\cos \left(\dfrac{2}{x} \right)} \\\\ &&\qquad \boxed{ \cos \left(\dfrac{6}{x} \right)-\cos \left(\dfrac{2}{x} \right) = -2\sin \left( \dfrac{6+2}{x} \above 1pt 2 \right) \sin \left( \dfrac{6-2}{x}\above 1pt 2 \right) \\~\\= -2\sin \left(\dfrac{4}{x} \right) \sin \left(\dfrac{2}{x} \right) } \\\\ &=& \dfrac{\sin^2 \left(\dfrac{4}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } {-2\sin \left(\dfrac{4}{x} \right) \sin \left(\dfrac{2}{x} \right)} \\\\ &=& -\dfrac{\sin \left(\dfrac{4}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } {2 \sin \left(\dfrac{2}{x} \right)} \\\\ &=& -\dfrac{\sin \left(2\cdot \dfrac{2}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } {2 \sin \left(\dfrac{2}{x} \right)} \\\\ &&\qquad \boxed{ \sin \left(2\cdot \dfrac{2}{x} \right) = 2 \sin \left(\dfrac{2}{x} \right)\cos \left(\dfrac{2}{x} \right) } \\\\ &=& -\dfrac{ 2 \sin \left(\dfrac{2}{x} \right)\cos \left(\dfrac{2}{x} \right)\sec^2 \left(\dfrac{4}{x} \right) } {2 \sin \left(\dfrac{2}{x} \right)} \\\\ &=& \mathbf{-\cos \left(\dfrac{2}{x} \right)\sec^2 \left(\dfrac{4}{x} \right)} \\ \hline \end{array}\)

The guest above is me - JoshuaGreen.  Forgot log in.

 Thank you again. Your responses are really great. Every time you give me such useful information. Where do you get these hints? I need to know them all!

If it is wrong maybe the question asks the money that is earned by the end of 5th year Not the sum of all the money earned from 1st year till 5th year.

so it is: 

f(5)=30000*(1.05)^4

=36,465.1875

Try non-compound raise of 5% and see if that agrees with their answer! You never know what they had in mind !!

$30,000 + [$30,000 x 1.05 x (5 - 1) ] =$30,000 + $126,000 = $156,000.

It is NOT really 5% annual raise after the first year but more like 4.66% annual raise!.

If a*b=2a+3b for all a and b, then what is the value of 4*3

\(\begin{array}{|rcll|} \hline 4*3 &=& 2\cdot 4 + 3\cdot 3 \\ &=& 8+9 \\ &=& \mathbf{17} \\ \hline \end{array}\)

It should work like this:
\(f(5, 3) = 555 \\ f(12,3)=121212 \\ \\ 555=5\cdot10^2+5\cdot10^1+5\cdot10^0 \\ 121212=12\cdot10^4+12\cdot10^2+12\cdot10^0 \)

We see that the power of ten dependence on the length of the number that we're repeating.

Knowing this we can bring out the formula.

\(rep\left(x,n\right)=\sum_{c=0}^{n-1}x\cdot10^{c\lfloor\log_{10}x\rfloor}\)

Where  (x is the repeating number)

Where  (n is the number of repetitions)

\(\lfloor log_{10}x\rfloor\) - length of x

Sorry there is a mistake:

The length of \(x\) is \(\mathbf{\lfloor log_{10}x\rfloor +\color{red} 1 }\)

\(\large{rep\left(x,n\right)=\sum \limits_{c=0}^{n-1}x\cdot10^{c \left( \lfloor\log_{10}x\rfloor+1 \right) }}\)

see Desmos:

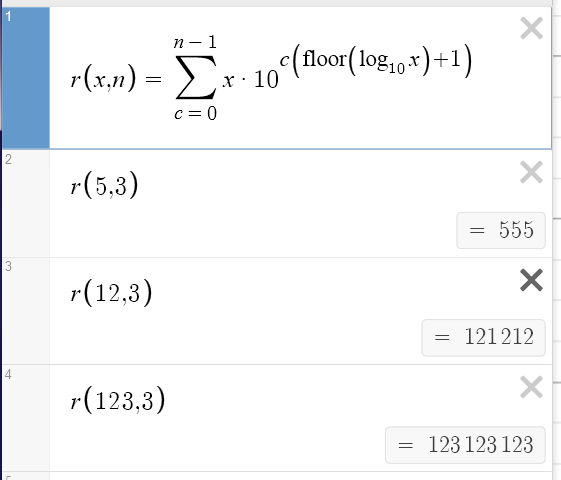
hint:

\(\begin{array}{|rcll|} \hline &&\mathbf{ \lfloor\log_{10}x\rfloor+1 } \\ &=& \lfloor\log_{10}x+1 \rfloor \\ &=& \lfloor\log_{10}x+\log_{10}(10) \rfloor \\ &=&\mathbf{ \lfloor\log_{10}(10x) \rfloor } \\ \hline \end{array}\)

see Desmos:

It will be 0 

Using directed subs, x=900,1000,1100 you will approach 0. 

Same here....that is the answer i got.

That's what I get.

What's the answer they give?

\(4x^2+ 3y^2 - 16x + 9y + 16 = 0\\ 4(x^2 - 4x) + 3(y^2 + 3y) + 16 = 0\\ 4(x^2 - 4x + 4 - 4) + 3\left(y^2 + 3y+\dfrac 9 4 - \dfrac 9 4\right) + 16 = 0\\ 4(x-2)^2 - 16 + 3\left(y+\dfrac 3 2\right)^2- \dfrac{27}{4}+16 = 0\\ \left(\dfrac{x-2}{\frac 1 2}\right)^2 + \left(\dfrac{y+\frac 3 2}{\frac{1}{\sqrt{3}}}\right)^2 = \left(\dfrac{3\sqrt{3}}{2}\right)^2 \)

You are welcome!   ~EP

\(\text{$x$ is the number of lawns mowed, and $y$ is the number of dogs walked}\\ 25x+15y \geq 1975\\ y \leq 4 x\\ y \geq 50\)

I see... the * isn't multiplication....

It would have been far clearer if you had either stated that up front or used a different symbol.

i absolutely agree with rom!