All Answers 356005 Answers

Let \(A\) be a matrix, and let \(x\) and \(y\) be vectors such that neither is a scalar multiple of the other and such that

\(\mathbf{A} \mathbf{x} = \mathbf{y},\ \mathbf{A} \mathbf{y} = \mathbf{x} + 2\mathbf{y}\).
Then we have that \(\mathbf{A}^5 \mathbf{x} = a \mathbf{x} + b\mathbf{y}\) for some scalars \(a\) and \(b\).
Find \(a\) and \(b\).

\(\begin{array}{|rcll|} \hline \mathbf{A} \mathbf{x} &=& \mathbf{y} \quad &| \quad \times \mathbf{A} \\ \mathbf{A}^2\mathbf{x} &=& \mathbf{A} \mathbf{y} \quad &| \quad \mathbf{A} \mathbf{y} = \mathbf{x} + 2\mathbf{y} \\ \mathbf{A}^2\mathbf{x} &=& \mathbf{x} + 2\mathbf{y} \\\\ \hline \mathbf{A}^2\mathbf{x} &=& \mathbf{x} + 2\mathbf{y} \quad &| \quad \times \mathbf{A} \\ \mathbf{A}^3\mathbf{x} &=& \mathbf{A}\mathbf{x} + 2\mathbf{A} \mathbf{y} \quad &| \quad \mathbf{A} \mathbf{x}=\mathbf{y},\ \mathbf{A} \mathbf{y} = \mathbf{x} + 2\mathbf{y} \\ \mathbf{A}^3\mathbf{x} &=& \mathbf{y} + 2( \mathbf{x} + 2\mathbf{y} ) \\ \mathbf{A}^3\mathbf{x} &=& \mathbf{y} + 2\mathbf{x} + 4\mathbf{y} \\ \mathbf{A}^3\mathbf{x} &=& 2\mathbf{x} + 5\mathbf{y} \\\\ \hline \mathbf{A}^3\mathbf{x} &=& 2\mathbf{x} + 5\mathbf{y} \quad &| \quad \times \mathbf{A} \\ \mathbf{A}^4\mathbf{x} &=& 2\mathbf{A}\mathbf{x} + 5\mathbf{A}\mathbf{y} \quad &| \quad \mathbf{A} \mathbf{x}=\mathbf{y},\ \mathbf{A} \mathbf{y} = \mathbf{x} + 2\mathbf{y} \\ \mathbf{A}^4\mathbf{x} &=& 2\mathbf{y} + 5( \mathbf{x} + 2\mathbf{y} ) \\ \mathbf{A}^4\mathbf{x} &=& 2\mathbf{y} + 5\mathbf{x} + 10\mathbf{y} \\ \mathbf{A}^4\mathbf{x} &=& 5\mathbf{x} + 12\mathbf{y} \\\\ \hline \mathbf{A}^4\mathbf{x} &=& 5\mathbf{x} + 12\mathbf{y} \quad &| \quad \times \mathbf{A} \\ \mathbf{A}^5\mathbf{x} &=& 5\mathbf{A}\mathbf{x} + 12\mathbf{A}\mathbf{y} \quad &| \quad \mathbf{A} \mathbf{x}=\mathbf{y},\ \mathbf{A} \mathbf{y} = \mathbf{x} + 2\mathbf{y} \\ \mathbf{A}^5\mathbf{x} &=& 5\mathbf{y} + 12( \mathbf{x} + 2\mathbf{y} ) \\ \mathbf{A}^5\mathbf{x} &=& 5\mathbf{y} + 12\mathbf{x} + 24\mathbf{y} \\ \mathbf{A}^5\mathbf{x} &=& 12\mathbf{x} + 29\mathbf{y} \\ \hline \end{array} \)

\(\mathbf{a=12,\ b=29}\)

Use the following transformations:

\(x=\rho .\sin \theta. \cos \phi\\y=\rho .\sin \theta.\sin \phi\\z=\rho .\cos \theta\)

it 11 and 36

The graph of a cosine function shows a reflection over the x-axis, an amplitude of 5, a period of 6, and a phase shift of 0.25 to the right.

Which is the equation of the function described?

Find the sum of the infinite series

\(1+2\left(\dfrac{1}{1998}\right)+3\left(\dfrac{1}{1998}\right)^2+4\left(\dfrac{1}{1998}\right)^3+\cdots\)

\(\small{ \begin{array}{rclllllllllc} & & \mathbf{1}&\mathbf{+} & \mathbf{2\left(\dfrac{1}{1998}\right)} &\mathbf{+} & \mathbf{3\left(\dfrac{1}{1998}\right)^2} &\mathbf{+} &\mathbf{ 4\left(\dfrac{1}{1998}\right)^3} & \mathbf{+}&\mathbf{\cdots} \\\\ & & & & & & & & & & &\mathbf{\text{sum }=\dfrac{a}{1-r}} \\ &=& 1&+ & 1\left(\dfrac{1}{1998}\right)^1 &+ & 1\left(\dfrac{1}{1998}\right)^2 &+ & 1\left(\dfrac{1}{1998}\right)^3 &+&\cdots & \dfrac{1}{1-\dfrac{1}{1998}} \\\\ & & &+ & 1\left(\dfrac{1}{1998}\right)^1 &+ & 1\left(\dfrac{1}{1998}\right)^2 &+ & 1\left(\dfrac{1}{1998}\right)^3 &+&\cdots & \dfrac{\left(\dfrac{1}{1998}\right)^1}{1-\dfrac{1}{1998}} \\\\ & & & & &+ & 1\left(\dfrac{1}{1998}\right)^2 &+ & 1\left(\dfrac{1}{1998}\right)^3 &+&\cdots & \dfrac{\left(\dfrac{1}{1998}\right)^2}{1-\dfrac{1}{1998}} \\\\ & & & & & & & + & 1\left(\dfrac{1}{1998}\right)^3 &+&\cdots & \dfrac{\left(\dfrac{1}{1998}\right)^3}{1-\dfrac{1}{1998}} \\\\ & & & & & & & & & +&\ldots \\ \end{array} }\)

\(\begin{array}{|rcll|} \hline &&\mathbf{ 1+2\left(\dfrac{1}{1998}\right)+3\left(\dfrac{1}{1998}\right)^2+4\left(\dfrac{1}{1998}\right)^3+\cdots } \\\\ &=& \dfrac{1}{1-\dfrac{1}{1998}} + \dfrac{\left(\dfrac{1}{1998}\right)^1}{1-\dfrac{1}{1998}} + \dfrac{\left(\dfrac{1}{1998}\right)^2}{1-\dfrac{1}{1998}} + \dfrac{\left(\dfrac{1}{1998}\right)^3}{1-\dfrac{1}{1998}} +\cdots \\\\ &=& \dfrac{1}{1-\dfrac{1}{1998}} \left( 1+ \left(\dfrac{1}{1998}\right)^1+\left(\dfrac{1}{1998}\right)^2+\left(\dfrac{1}{1998}\right)^3 +\cdots \right) \\\\ &=& \dfrac{1}{\dfrac{1998-1}{1998}} \left( 1+ \left(\dfrac{1}{1998}\right)^1+\left(\dfrac{1}{1998}\right)^2+\left(\dfrac{1}{1998}\right)^3 +\cdots \right) \\\\ &=& \dfrac{1998}{1997} \left( 1+ \left(\dfrac{1}{1998}\right)^1+\left(\dfrac{1}{1998}\right)^2+\left(\dfrac{1}{1998}\right)^3 +\cdots \right) \\\\ &=& \dfrac{1998}{1997} \left( \dfrac{1}{1-\dfrac{1}{1998}} \right) \\\\ &=& \dfrac{1998}{1997} \left( \dfrac{1}{\dfrac{1998-1}{1998}} \right) \\\\ &=& \dfrac{1998}{1997}\times \dfrac{1998}{1997} \\\\ &=& \dfrac{1998^2}{1997^2} \\\\ &=&\mathbf{ \dfrac{3992004}{3988009}} \\ \hline \end{array}\)

I figured out the answer already, thank you tho!

Let \(a_0=6\) and \(a_n = \dfrac{a_{n - 1}}{1 + a_{n - 1}}\) for all \(n \ge 1\).
Find \(a_{100}\)

\(\begin{array}{|rcll|} \hline a_n &=& \dfrac{a_{n - 1}}{1 + a_{n - 1}} \\\\ \dfrac{1}{a_n} &=& \dfrac{1 + a_{n - 1}} {a_{n - 1}} \\\\ \dfrac{1}{a_n} &=& \dfrac{1} {a_{n - 1}} +\dfrac{a_{n - 1}} {a_{n - 1}} \\\\ \mathbf{\dfrac{1}{a_n}} &=& \mathbf{\dfrac{1} {a_{n - 1}} + 1} \\ \hline \end{array}\)

\(\begin{array}{|lrcll|} \hline \mathbf{\dfrac{1}{a_n}} = \mathbf{\dfrac{1} {a_{n - 1}} + 1} \\ \hline n=1: & \dfrac{1}{a_1} &=& \dfrac{1} {a_{1 - 1}} + 1 \\\\ & \mathbf{\dfrac{1}{a_1}} &=& \mathbf{ \dfrac{1} {a_{0}} + 1} \\ \hline n=2: & \dfrac{1}{a_2} &=& \dfrac{1} {a_{2-1}} + 1 \\\\ & \dfrac{1}{a_2} &=& \dfrac{1} {a_{1}} + 1 \\\\ & \dfrac{1}{a_2} &=& \dfrac{1} {a_{0}} + 1 + 1 \\\\ & \mathbf{\dfrac{1}{a_2}} &=& \mathbf{\dfrac{1} {a_{0}} + 2} \\ \hline n=3: & \dfrac{1}{a_3} &=& \dfrac{1} {a_{3-1}} + 1 \\\\ & \dfrac{1}{a_3} &=& \dfrac{1} {a_{2}} + 1 \\\\ & \dfrac{1}{a_3} &=& \dfrac{1} {a_{0}} + 2 + 1 \\\\ & \mathbf{\dfrac{1}{a_3}} &=& \mathbf{\dfrac{1} {a_{0}} + 3} \\ \hline \ldots \\ \hline & \mathbf{\dfrac{1}{a_n}} &=& \mathbf{\dfrac{1} {a_{0}} + n} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\dfrac{1}{a_n}} &=& \mathbf{\dfrac{1} {a_{0}} + n} \quad | \quad a_0 = 6 \\\\ \dfrac{1}{a_n} &=& \dfrac{1} {6} + n \quad | \quad n = 100 \\\\ \dfrac{1}{a_{100}} &=& \dfrac{1} {6} + 100 \\\\ \dfrac{1}{a_{100}} &=& \dfrac{1} {6} + \dfrac{600}{6} \\\\ \dfrac{1}{a_{100}} &=& \dfrac{1+600} {6} \\\\ \dfrac{1}{a_{100}} &=& \dfrac{601} {6} \\\\ \mathbf{ a_{100} } &=& \mathbf{\dfrac{6}{601} } \\ \hline \end{array}\)

m^2 = sqrt(3)/2.

\(\mathbf{A} \begin{pmatrix} 1 \\ -1 \\ -1 \end{pmatrix} = \mathbf{A} \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} - \mathbf{A} \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} -3 \\ 4 \\ 0 \end{pmatrix} - \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} -4 \\ 2 \\ -3 \end{pmatrix}\)

By power of a point, the smallest possible value of CQ is 8.

Angle C = 180 - 23 = 157 degrees.

The intersections are (12/13*(3*sqrt(3) - 1),6/13*(3 + 4*sqrt(3)) and (-12/13*(1 + 3sqrt(3)), -6/13*(4*sqrt(3) - 3), so the length of the chord is sqrt((12/13*(3*sqrt(3) - 1 + 12/13*(1 + 3*sqrt(3))^2 + (6/13*(3 + 4*sqrt(3)) + 6/13*(4*sqrt(3) - 3))^2) = 24*sqrt(39)/13.

1)    Figure 0  should have  6 tiles

2)    6 + 12 = 18         12 + 18 = 30        18 + 30 = 48   ....and so on  

3)   Figure  -1  should have 6 tiles also     6 + 6 = 12

      Figure  -2   should have  0  tiles  because   0 + 6 = 6   

A circle with radius 6 has a sector with a central angle of 48º.  What is the area of the sector?

Area of the sector:   A = [ (r² * pi) / 360 ] * 48  

2)    Angle  EDC = 15º  

The following post is extremely incorrect. If you can identify what is wrong, then great job then help me take down the mathcounts organization.

The formula for infinite series stuff (Mathcounts and AMC 8 has done horrible things to my mind, teaching me to memeroize formulas instead of proving and figuring out myself).

\(\frac{a(1)}{1-r}\)

a(1) = first term

What do you think the first term is? (this one is a brain breaker!)

r = common ratio

Find the common ratio by dividing the second term by the first term.

Plug n' solve! 

If you open the bag and look inside, and if you have intentions of picking first a green jelly bean then a red one, the probability surely will be 100% (Am I right or am I right?)

In fraction form:

What are the odds of the first jelly bean being green?

What are the odds of the seconds jelly being red? (The total number of jelly beans should be one less than when you picked a green one)

You then multiply the fractions together... am I right or am I wrong?

oh yey geometry where I can use my faulty intuition

AB//CD

ED//BC

AE//BD

Theorem (in my own words): Two triangles have the same area if they share a base and their height is presumably equal.

Count all the triangles that have base AB that has the other two sides joining on a point lying on line DC

Count all the triangles that have base DB that has the other two sides joining on a point lying on the line EA

Count all the triangles that have the base AD that has the other two sides joining on a point lying on.... oh wait! AD is NOT parrelel to BD. So there is only one triangle for this case.

thanks man

Strong work CU !!         (at least we BOTH got the same answer !)

Oh dang I got it correct now my self-esteem inflated

Apologies, I am jumping at this problem with only knowledge up to High School Geometry Right Triangle Trigonometry Unit (yes, I am an uneducated idot, deal with it.)

According to my inaccurate intuition, if he swam at an angle, his path will be circular (or elliptical?). I am to proceed with this inaccurate intuition.

I drew the following image on Scratch. (Yes, my hobby is making video games then getting addicted to my own video games)

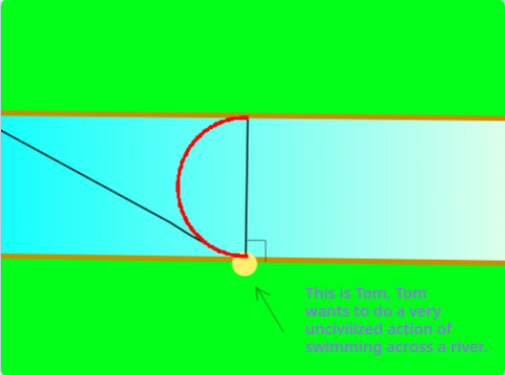
So the angle he swims at shall be tangent to that semi-circular path? I think my intuition serves me incorrectly.

At this point, I realize my intuition was unreliable and I decided to look up the answer on Chegg. Unfortunately, I do not own a Chegg account, so I refused the $20 monthly fee as confronting my parents to give me 20 bucks a month to help someone online with a math problem wouldn't be a wise decision.

Again using my amazing intuition, I imagine Tom swimming straight forward at 2km/h with the river pushing him at 1km/h. 

According to my intuition, he will have moved down the river 250 meters when he crossed the 500 meter wide river.

Alright, then using my intuition once again, the angle in which he must swim at to offset that 250 meters is basically the angle formed by a triangle whose legs are in a 1:2 ratio.

So by finally using something else then my intuition, I used a calculator (hence my name) and calculated for this:

\(tan^{-1}(\frac{1}{2})\)

asin(1/2) = 26.565051177078

So I got 90 - 26.565051177078 = WHATEVER THIS IS

In other words, I probably learn from someone else's answer if I am incorrect.

His resultant speed is    sqrt ( 1^2 + 2^2) = sqrt 5

he needs to swim at an angle....the distance he swims is the hypotenuse of a right triangle  and =   sqrt 5 t  

    where t is the time it takes him to cross....meanwhile the current moves him  1 km/hr * t

sin  = opp/hyp  =    1 t / (sqrt 5 * t) = 1/5

arcsin 1/5 = 26.56 degrees angled upstream       an angle of   90 - 26.56 =  63.43 degrees with the bank