All Answers 357312 Answers

Angela's Investment:  FV =$8,000 x 1.06^20 =$25,657.08 - principal + interest over 20 years.

Bob's Investment: $10,000 x 0.07 =$700 - simple interest earned in 1 year.

$700 x 20 years =$14,000 - Total simple interest earned over 20 years.

$10,000 + $14,000 =$24,000 - Bob's total principal + interest over 20 years

$25,657.08 -  $24,000 =$1,657.08 - difference in interest earned over 20 years.

n%5==4 and n%6==5 and n%7==6 and n%8==7 and n%9==8

The LCM(5,6,7,8,9) =2520

2520 - 1 = 2519

The smallest n = 2519

if you just type it in then it would only be ^\circ but if you click on the latex button then you type ^\circ then it will be $^\circ$

I think you should use the latex ^\circ to do the degree sign in latex $^\circ$

Not sure exactly what you are asking....

  I use the superscript  o         like   225^o

FG is similar to TS   as    GH is to SR

104/39 = GH/30

GH = 30 * 104/39 = .......

Get the area of the   6 x 6  square.... then subtract the two unshaded triangles     area of a triangle = 1/2 b h      

Instead of solving that (which I don't think anyone has the time for), we could just find the units digits of all those numbers and add and subtract them. 

How to we do that? Well, we know that 19^1 has a unit digit 9, and 19^2 has a unit digit 1, 19^3 has unit digit 9, 19^4 has unit digit 1... you see the patern? Every odd power has unit digit of 9, and even power gives unit digit of 1. Do the same thing with 11: 11^1 : 1, 11^2 : 1, 11^3 : 1... we see that every unit digit of a power of 11 gives 1. Now for 6: 6^1 : 6, 6^2 : 6, 6^3 : 6... same thing here, we see that the unit digit is 6 for every power of 6. 

So, now we do 1+1, which is 2. Borrow a 10 from the tenths place, 12-6 is 6. Therefore, the unit's digit is $\boxed{6}$

This involves casework. So, let's first see how many options there are for 5 digits:

This is basically 10 to the power of 5 (ten numbers from 0-9, and you can repeat, so 10(10)(10)(10)(10), which is 10^5), which is 100,000

The line through (7,8) and (9,0) can be written as y = mx + c, where m and c are constants found from the following:

8 = 7m + c

0 = 9m + c

Hence 2m = -8 or m = -4, so c = 8 + 7*4 = 36

Therefore the line is described by  y = -4x + 36

Now equate this and y = 2x - 10 to find the values of x (=a) and y (=b) that satisfy both equations.

A - B = 4, 

B + A^2=86, solve for A, B

A =9   and   B =5

xxxxxxx

Here is one sequence that satisfies all the coditions in your question. And here is the "closed form"  formula that generates each term:
a(n) = 1/2 (4 n + (-1)^n + 5) 
Sum=(4, 7, 8, 11, 12, 15, 16, 19, 20, 23, 24, 27, 28, 31, 32, 35, 36, 39, 40, 43) = 470
The odd-numbered terms sum up to 220, while the even-numbered terms sum up to 250 and the total sum of the sequence is 470.
The two "middle terms" are: 23 and 24
Note: This may not be the sequence that you have, but it is just as valid as any other sequence.

What do you think?

Here is a simple site that I would probably use for this.

$\lambda$ is the Greek letter lambda.

Angle  GPF = 90 degrees

Angle  E = 20.5 degrees

Here is a picture of Alan's answer:  Sorry, it is a bit small ....

Using the Euclidian Algorithm, calculate $\gcd(2^{60}-1, 2^{80}-1)$

Formula: $\boxed{ \gcd(a,b) = \gcd(b,a) \\~\\ \gcd(a,b) = \gcd(a-n*b,b) \\~\\ \gcd(a,a) = a }$

$\begin{array}{|rcll|} \hline && \mathbf{\gcd\left( 2^{60}-1,~ 2^{80}-1 \right)} \\ &=& \gcd\left( 2^{80}-1,~ 2^{60}-1 \right) \\ && \begin{array}{|rcll|} \hline 2^{80}-1 &=& 1+2+2^2+2^3+\ldots+2^{79} \\ 2^{60}-1 &=& 1+2+2^2+2^3+\ldots+2^{59} \\ \hline 2^{20}*(2^{60}-1) &=& 2^{20}+2^{21}+\ldots+2^{79} \\ \hline \mathbf{ (2^{80}-1)-2^{20}*(2^{60}-1)} &=& \mathbf{1+2+2^2+2^3+\ldots+2^{19}} \\ \mathbf{ (2^{80}-1)-2^{20}*(2^{60}-1)} &=& \mathbf{2^{20}-1} \\ \hline \end{array} \\ &=& \gcd\left( (2^{80}-1)-2^{20}*(2^{60}-1),~ 2^{60}-1 \right) \\ &=& \mathbf{ \gcd\left( 2^{20}-1,~ 2^{60}-1 \right) } \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline && \mathbf{ \gcd\left( 2^{20}-1,~ 2^{60}-1 \right) } \\ &=& \mathbf{ \gcd\left( 2^{60}-1,~ 2^{20}-1 \right) } \\ && \begin{array}{|rcll|} \hline 2^{60}-1 &=& 1+2+2^2+2^3+\ldots+2^{59} \\ 2^{20}-1 &=& 1+2+2^2+2^3+\ldots+2^{19} \\ \hline 2^{40}*(2^{20}-1) &=& 2^{40}+2^{41}+\ldots+2^{59} \\ \hline \mathbf{ (2^{60}-1)-2^{40}*(2^{20}-1)} &=& \mathbf{1+2+2^2+2^3+\ldots+2^{39}} \\ \mathbf{ (2^{60}-1)-2^{40}*(2^{20}-1)} &=& \mathbf{2^{40}-1} \\ \hline \end{array} \\ &=& \gcd\left( (2^{60}-1)-2^{40}*(2^{20}-1),~ 2^{20}-1 \right) \\ &=& \mathbf{ \gcd\left( 2^{40}-1,~ 2^{20}-1 \right) } \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline && \mathbf{ \gcd\left( 2^{40}-1,~ 2^{20}-1 \right) } \\ && \begin{array}{|rcll|} \hline 2^{40}-1 &=& 1+2+2^2+2^3+\ldots+2^{39} \\ 2^{20}-1 &=& 1+2+2^2+2^3+\ldots+2^{19} \\ \hline 2^{20}*(2^{20}-1) &=& 2^{20}+2^{21}+\ldots+2^{39} \\ \hline \mathbf{ (2^{40}-1)-2^{20}*(2^{20}-1)} &=& \mathbf{1+2+2^2+2^3+\ldots+2^{19}} \\ \mathbf{ (2^{40}-1)-2^{20}*(2^{20}-1)} &=& \mathbf{2^{20}-1} \\ \hline \end{array} \\ &=& \gcd\left( (2^{40}-1)-2^{20}*(2^{20}-1),~ 2^{20}-1 \right) \\ &=& \mathbf{ \gcd\left( 2^{20}-1,~ 2^{20}-1 \right) } \\ &=& 2^{20}-1 \\ &=& \mathbf{1048575} \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline && \mathbf{\gcd\left( 2^{60}-1,~ 2^{80}-1 \right)} \\ &=& \mathbf{ \gcd\left( 2^{60}-1,~ 2^{20}-1 \right) } \\ &=& \mathbf{ \gcd\left( 2^{40}-1,~ 2^{20}-1 \right) } \\ &=& \mathbf{ \gcd\left( 2^{20}-1,~ 2^{20}-1 \right) } \\ &=& \mathbf{2^{20}-1} \\ &=& \mathbf{1048575} \\ \hline \end{array}$

$y=\frac{1}{\sqrt2}-(x^2-3)\\ y=-x^2+3+\frac{1}{\sqrt2}\\ y=-x^2+\frac{6+\sqrt2}{2}\\ $

This is a concave down parabola with y intercept     $\frac{6+\sqrt2}{2}\approx 3.707$

And the y axis is the axis of symmetry.

A general point on this parabola is    $(x,\left[-x^2+\frac{6+\sqrt2}{2}\right])\\$

The distance square from (0,0) to the parabola for any given x value will be

$d^2=D=(x-0)^2+(-x^2+\frac{6+\sqrt2}{2}-0)^2\\ D=x^2+(-x^2+\frac{6+\sqrt2}{2})^2\\ D=x^2+x^4+(-2*\frac{6+\sqrt2}{2})x^2+(\frac{6+\sqrt2}{2})^2\\ D=x^2+x^4+(-6-\sqrt2)x^2+(\frac{36+2+12\sqrt2}{4})\\ D=x^4+(1-6-\sqrt2)x^2+(\frac{19}{2}+3\sqrt2)\\ D=x^4+(-5-\sqrt2)x^2+(\frac{19}{2}+3\sqrt2)\\~\\ D'=4x^3+2(-5-\sqrt2)x\\ \text{D will be minimum when }D'=0\\ 0=4x^3+2(-5-\sqrt2)x\\ \text{I know just from thinking about the graph that }\;x\ne0\\ 0=4x^2+2(-5-\sqrt2)\\ 0=4x^2-10-2\sqrt2\\ 4x^2=10+2\sqrt2\\ 2x^2=5+\sqrt2\\ x^2=\frac{5+\sqrt2}{2}\\ x=\pm\sqrt{\frac{5+\sqrt2}{2}}\\$

So the distance will be minimum when     $x=\pm\sqrt{\frac{5+\sqrt2}{2}}\\$

Sub to get y

$y=-\left[\pm\sqrt{\frac{5+\sqrt2}{2}}\right]^2+\frac{6+\sqrt2}{2}\\ y=-\left[\frac{5+\sqrt2}{2}\right]+\frac{6+\sqrt2}{2}\\ y=\frac{-5-\sqrt2}{2}+\frac{6+\sqrt2}{2}\\ y=\frac{1}{2}$

So the closest points on the parabola to (0,0)     are      $\left(\sqrt{\frac{5+\sqrt2}{2}},\frac{1}{2}\right)\quad and \quad \left(-\sqrt{\frac{5+\sqrt2}{2}},\frac{1}{2}\right)$

So the distance from either both these points to the origin will be    

$d=\sqrt{          \left(\frac{5+\sqrt2}{2}\right)   + \frac{1}{4}       }\\ d=\sqrt{          \left(\frac{10+2\sqrt2+1}{4}\right) }\\ d=\sqrt{          \left(\frac{11+2\sqrt2}{4}\right) }\\ smallest\;\; distance=\frac{\sqrt{  11+2\sqrt2  }}{2}\\ smallest\;\; distance\approx 1.86\;units$

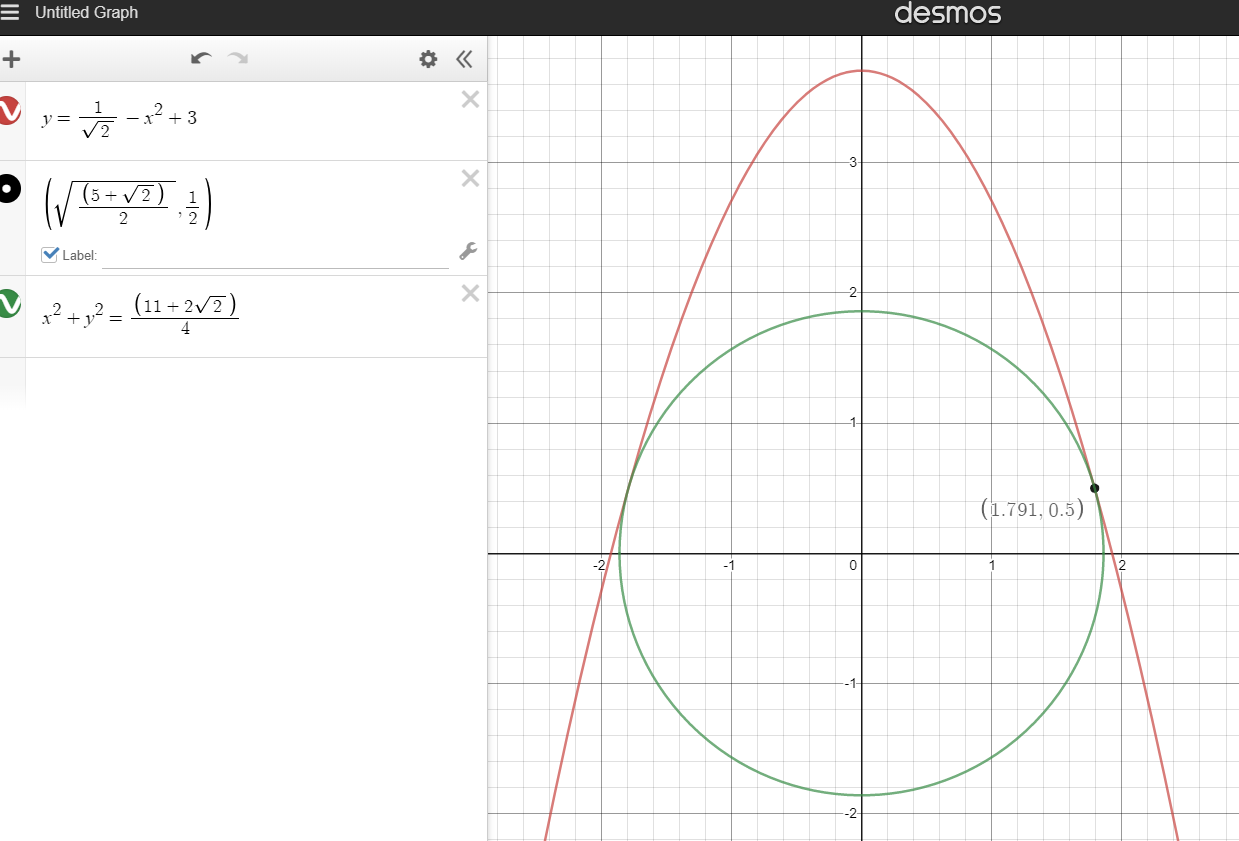
Here is the related graph:

LaTex:

y=\frac{1}{\sqrt2}-(x^2-3)\\
y=-x^2+3+\frac{1}{\sqrt2}\\
y=-x^2+\frac{6+\sqrt2}{2}\\

d^2=D=(x-0)^2+(-x^2+\frac{6+\sqrt2}{2}-0)^2\\
D=x^2+(-x^2+\frac{6+\sqrt2}{2})^2\\
D=x^2+x^4+(-2*\frac{6+\sqrt2}{2})x^2+(\frac{6+\sqrt2}{2})^2\\
D=x^2+x^4+(-6-\sqrt2)x^2+(\frac{36+2+12\sqrt2}{4})\\
D=x^4+(1-6-\sqrt2)x^2+(\frac{19}{2}+3\sqrt2)\\
D=x^4+(-5-\sqrt2)x^2+(\frac{19}{2}+3\sqrt2)\\~\\
D'=4x^3+2(-5-\sqrt2)x\\
\text{D will be minimum when }D'=0\\
0=4x^3+2(-5-\sqrt2)x\\
\text{I know just from thinking about the graph that  }\;x\ne0\\
0=4x^2+2(-5-\sqrt2)\\
0=4x^2-10-2\sqrt2\\
4x^2=10+2\sqrt2\\
2x^2=5+\sqrt2\\
x^2=\frac{5+\sqrt2}{2}\\
x=\pm\sqrt{\frac{5+\sqrt2}{2}}\\

y=-\left[\pm\sqrt{\frac{5+\sqrt2}{2}}\right]^2+\frac{6+\sqrt2}{2}\\
y=-\left[\frac{5+\sqrt2}{2}\right]+\frac{6+\sqrt2}{2}\\
y=\frac{-5-\sqrt2}{2}+\frac{6+\sqrt2}{2}\\
y=\frac{1}{2}

\left(\sqrt{\frac{5+\sqrt2}{2}},\frac{1}{2}\right)\quad and \quad \left(-\sqrt{\frac{5+\sqrt2}{2}},\frac{1}{2}\right)

d=\sqrt{          \left(\frac{5+\sqrt2}{2}\right)   + \frac{1}{4}       }\\
d=\sqrt{          \left(\frac{10+2\sqrt2+1}{4}\right) }\\
d=\sqrt{          \left(\frac{11+2\sqrt2}{4}\right) }\\
smallest\;\; distance=\frac{\sqrt{  11+2\sqrt2  }}{2}\\
smallest\;\; distance\approx 1.86\;units