All Answers 358144 Answers

From the product formula, the product works out to n^((n + 3)/2), so a + b + c = 1 + 3 + 2 = 6.

Yes, I am sorry I had it wrong and I think I wasted everyone's time. I was struggling with it and thought I was missing something, and now I know what it was the "-" sign.

There are 28 possible combinations.

https://web2.0calc.com/questions/please-help-asap-and-explain

9C2 committies

WXYZ is a parallelogram where angle W is half of a right angle WX = 10, and XY = 144, What is the area of the parallelogram.

[WXYZ] = XY * √50

sumfor(n, 1, 100, floor(2#(n))==625

How do you know that AE = 4???

Triangle sides are      a = 4,   b = 5,  and   c = 6

Semiparameter    s = 7.5

Triangle area    A = 9.922

Inradius        r = A / s = 1.323

Circumradius     R = (abc) / (4rs) = 3.024

R / r = 16 / 7

I believe you mean y = -x + 6, since this is worded exactly like an alcumus problem I saw a few days ago.

Anyway, the solution I did was:

The slope of the line from the origin to the point Q must be perpendicular to the slope of the line from (10, -10) to the point Q.

The equation for that is: \(\frac{x}{y} = - \frac{-10-y}{10-x}\)

Replace y with -x + 6 to solve for x:

\(\frac{x}{-x+6} = -\frac{-10-(-x+6)}{10-x}\\\frac{x}{-x+6} = \frac{16-x}{10-x} \\ 10x-x^2=x^2-22x+96\\ 2x^2-32x+96=0\\x^2-16x+48=0\\(x-4)(x-12)=0\\x=4, x=12\)

The y values corresponding to these x values are \(y = 2, y = -6\), respectively.

Therefore, the answer to this question is \(4+12+2-6=\boxed{12}\)

https://www.desmos.com/calculator/efz9crqvir (this will help you visualize it)

E = hf         E = energy    h = planck constant (use the value in your question)     f = frequency = 77x 10⁶

There are 14 different amounts.

AM = 1/2 (BC)        ∠ABM ≅ ∠BAM         ΔABC ~ ΔAMF

[AFDE] = 15.625 square units

I don't believe this is  possible, geoNewbie

The  hypotenuse  will  be  the  fixed distance   from O to  A =   sqrt (10^2 + 10^2)  = sqrt (200)  =OA

Call the point  that we seek  ( x, x+ 6)

The distance  from    O to Q =    sqrt  [ ( x^2  + ( x + 6)^2  ]  =  OQ

And the distance  from   A to Q  = sqrt  [ ( x - 10) +  ( x + 6  - - 10)^2 ]  =

sqrt  [ (x - 10)^2  + (x + 16)^2 ]  =   AQ

Using the Law of Cosines   we  have that

OA^2   =  OQ^2  + AQ^2  - 2( OQ  * AQ)  cos (90)

The  cos 90   =  0     so  this boils down to

OA^2 =  OQ^2  + AQ^2

200   = ( x^2  + (x + 6)^2  +  ( x - 10)^2  + ( x + 16)^2

Using WolframAlpha to solve this, we get  no real solutions  for  x

Also.....playing around with this triangle in Geogebra, I  couldn't find any  angles   of OQA even approaching 90°

In fact  about   the  largest angle I could find is  ≈  38.xxx °

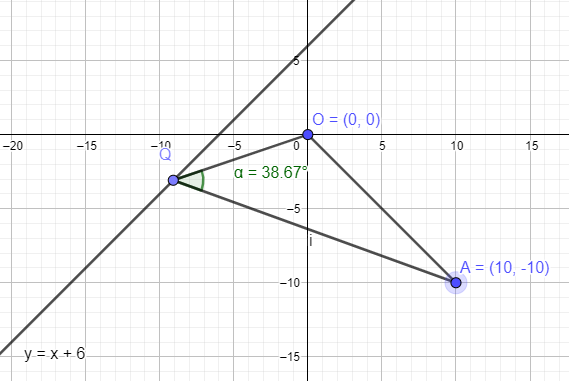
I wonder if  you might not mean  angle  QOA   is the right angle   ????

your welcome :)

Thank you bro!!!

You are welcome !

z = (obs - emit )/emit

  =  (141-126)/126 = .119    (positive =   red shift)

if v is much less than c then   z~~ v/c

.119 = v/3x10^8

v = 3.57 x 10⁷ m/s = 3.57 x10⁴ km/s       (ignoring the Lorentz factor)

Thank you!!!

1903 cal * 4184 j/cal = 7962152 j      per day

1 watt = 1 j / sec

7962152 j / (3600*24 sec)= 92.15 watts         (3600 * 24 is the number of seconds in a day)

Thank you :D

Thank you sm!!!