All Answers 356779 Answers

See the following  image  :

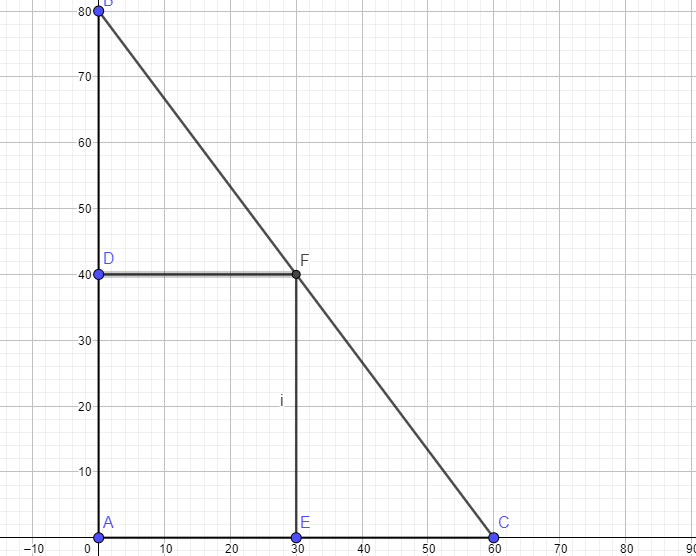
Let  x be the width of such a  building

The segment  BC  has  a  slope  of   (-80) / (60)  =  -8/6  = -4/3

And the  equation  of  a line theorugh this segmnt has the  equation  y = (-4/3) ( x - 60)

Note  that at any point x,  the length  of the  building will  be  equal   to this "y"

So.....the  area of such a  building  is  x * y  =    x [ ( -4/3) (x -60) ]

So

Area   =    (-4/3) (x) ( x -60)  =    (-4/3)x^2  + 80x

This is a parabola that  turns  downward

The  "x"   that will maximize  the   area =  the x coordinate  of the  vertex  =     -80  / (2 *-4/3)   =  80 / (8/3)  = 240 / 8 =  30 m

And  the  max area is     (-4/3)(30)^2  + 80 (30)  =  -1200  +  2400  =   1200 m^2

{The building is denoted  by ADFE}

What is the ratio of the area of triangle $BXY$ to the area of triangle ABC?

Hello Guest!

\(sin(45°)=\frac{1}{2}\cdot \sqrt{2}=\frac{\overline{XY}}{12}\)

\(\overline{XY}=6\cdot \sqrt{2}\)

\(\overline{BC}=18\)

\(A_{BXY}:A_{ABC}=\frac{1}{2}\cdot \overline{XY}^2:\frac{1}{2}\cdot \overline{BC}^2\)

\(A_{BXY}:A_{ABC}=\frac{1}{2}\cdot 72:\frac{1}{2}\cdot 324\)

\(A_{BXY}:A_{ABC}=2:9\)

  !

Have you done calculus yet?

Nice try guest answerer but you have not taken into account that the population reduces each year, so the actual decrease in numbers is not going to be exactly the same every year.  It will steadily get less.  So your answer will be too low.

459 * (1-0.035)^15

= 459 * 0.965^15

= 269 bears

Use the fact that tan = opposite/adjacent, so here:

tan(37º) = 72/X  

Rearrange to find X.

Some of my LaTex, (therefore some of my answer) has disappeared     

Let f(x)= 2 / sqrt(x). What is the domain of f? Express your answer with interval notation.

Hello mintjellyxd!

\(the\ domain\ of\ (f(x)=\frac{1}{\sqrt{x}})\subset \mathbb R | 0 < x < ∞\)

  !

\(\)

Hi Kitt,

What you have described in words is a combination

For example, 3 people are chosen from 10.  How many COMBINATIONS are possible   10C3=120   would be the answer?

For permutations, order matters.

For example.  10 people run in a race, how many PERMUTATIONS are possible for 1st, 2nd and 3rd places.

This is the same as:  choose 3 from 10 when order matters.     10P3=720 ways.

We know $CE \times DB = CB \times DC$ because area of triangles

DB is 6 cuz DBC is 30 60 90

$6 \times CE = 3\sqrt{3}$

$CE = \sqrt{3}/2$

It was a hard question so I wanted to make sure it wasn't a trick question

ok, that is a bit weird but at least I understand what you did now.  Thanks :)

I just set $h(x)$ as a function that fits the question

The link doesn't work, you need to be able to sign in.

They probably do not want you to get outside help anyway.

I got 32 as well but I do not understand your logic.

I just said that for the g function

\(-8\le\frac{x}{2}\le8\\ so\\ -16\le x\le16\\\)

width =32

I assume it is 2

6 and 7 are both in the vertical middle so they don't count.

1+3=2+2

I think 218.025 becasue 3.5% of 459 is 16.065. 16.065x15 is 240.975. 459-240.975 = 218.025.

There are 84 possible paths.

Answer:

\( \begin{array}{cc} 2 & 3 \\ 3 & 1 \end{array} \)

a = 340.

This is easy using coordinates.

This is easy.  I solved it using coordinates.

The axis of symmetry is x = -6.

hoo boy. please don't tell me this is a joke

1) 6^2=36 and 3^3=27 so 36-27=9

2) the first two positive even numbers are 2+4=6 (note: 0 is a neutral number) 

Try letting x = a and y = 1/b.  Then you should get the result that xyz can be -2, -1, 1 or 2.

n = 670.