From wikipedia:
In order to preserve the original rule:
for negative values of 
we must use the recursive relation:
Thus:
However smaller negative values cannot be well defined in this way because
which is not well defined.
Note further that for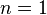 
any definition of 
is consistent with the rule because
for any 
. 
+130511 Another way to do this (more difficult) is to use the Secant-Tangent Theorem
Note, flflvm97, the line y = x + 3 doesn't actually intersect this circle, but the line y = x + √2 does.....
Call the y coordinate of R, "y".....using symmetry the distance between the two points where the line x = .75 intersects the circle = 2y
And using y = x+ √2, the x coordinate of the intercept of the line and the circle =
x^2 + (x + √2)^2 = 1
x^2 + x^2 + 2√2x + 2 = 1
2x^2 + 2√2x + 1 = 0
2x^2 + √8x + 1 = 0 and using the quad formula x = - √8/4 = -1/√2
And using y = x + √2, (-1/ √2)^2 + y^2 = 1 so y^2 = 1/2 and y = the positive root= 1/ √2
So the intersection of the line and the circle is ( -1/√2, 1/√2)
And when x = .75, the y coordinate of this point on the line is (.75 + √2)
And using the Secant-Tangent Theorem ,we have
( .75 + √2 + y)*(.75 + √2 - y) = (.75 + 1/ √2)^2 + (.75 + √2 - 1/ √2)^2
( .75 + √2 + y)*(.75 + √2 - y) = (.75 + 1/ √2)^2 + (.75 + 1/ √2)^2
(.75 + √2)^2 - y^2 = 2 (.75 + 1/ √2)^2
So
y^2 = (.75 + √2)^2 - 2 (.75 + 1/ √2)^2
And y = ±√((.75 + √2)^2 - 2 (.75 + 1/ √2)^2) = ±.661438 = ±√(7)/4
And choose the positive root.....and this is the y coordinate of "R".....so R = (3/4, √(7)/4)
(I told you it was more difficult !!!)
