There is a theorem that would be very helpful to know here. It is called the triangle exterior angle theorem. It states that the exterior angle is equal to the measure of the two remote (angle opposite the exterior) angles. This definition may be hard to understand, but a diagram would probably be useful. It may not be the neatest drawing, but you should understand the concept.
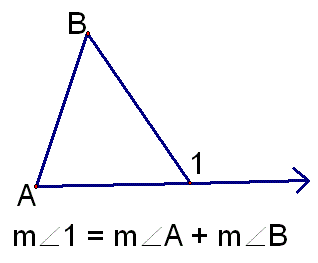
Now, let's use this to our advantage. Because of the triangle exterior angle theorem, we know that \(m\angle PAB=m\angle B+m\angle C\). Now that we have an equation that relates all the angles together, we can do the process of solving!
| \(m\angle PAB=m\angle B+m\angle C\) | We have already derived this equation. Now, substitute the values given for each angle. |
| \(x=90+mx+n\) | Now, substitute 1 for m, as given in the original description of the equation. |
| \(x=90+x+n\) | Subtract x from both sides. |
| \(0=90+n\) | Subtract 90 from both sides. |
| \(n=-90\) | |
Now, of course, we know that m=1 and n=-90. If you add those 2 values together, you get that \(m+n=1+(-90)=-89\)
.This diagram has a lot of information, and it can be somewhat difficult to decipher. With 2 radii, it should be possible to figure out the central angle. Before we start, we must understand arc length and its formula. The formula is below
\(\text{Arclength}=\frac{m^{\circ}}{360^{\circ}}*2\pi r\)
m = measure of the central angle, in degrees
r = radius of the circle
First, let's create 2 equations that demonstrate the relationship of r1 in this diagram:
| \(l=\frac{m^{\circ}}{360^{\circ}}*2\pi r\) | I am using "l" as my chosen variable for arc length. Of course, we already know the arc length; it is A, or 32. And we know that arc length corresponds with r1. |
| \(32=\frac{m^{\circ}}{360^{\circ}}*2\pi r_1\) | Great! Now, I will solve for r1 now. First, let's simplify the right hand side of the equation. |
| \(\frac{m^{\circ}}{360^{\circ}}*\frac{2\pi r_1}{1}\) | Multiply the fractions together. |
| \(\frac{2\pi r_1 m^{\circ}}{360^{\circ}}\) | The numerator and denominator have a GCF of 2, so factor that out. |
| \(\frac{\pi r_1 m^{\circ}}{180^{\circ}}\) | Reinsert this into the orginal equation. |
| \(32=\frac{\pi r_1 m^{\circ}}{180^{\circ}}\) | Multiply by 180 on both sides of the equation. |
| \(5760^{\circ}=\pi r_1 m^{\circ}\) | Divide by \(\pi m^{\circ}\) to isolate r1 |
| \(r_1=\frac{5760^{\circ}}{\pi m^{\circ}}\) | |
Let's do the exact same process for r2.
| \(34=\frac{m^{\circ}}{360^{\circ}}*2\pi r_2\) | We already from before what the right hand side simplifies to, so let's do that. |
| \(34=\frac{\pi r_2 m^{\circ}}{180^{\circ}}\) | Do the same process to solve for r2. Multiply both sides by 180. |
| \(6120^{\circ}=\pi r_2 m^{\circ}\) | Divide both sides by \(\pi m^{\circ}\). |
| \(r_2=\frac{6120^{\circ}}{\pi m^{\circ}}\) | |
We have two equations, and they are the following:
{
\(r_2=\frac{6120^{\circ}}{\pi m^{\circ}}\)
\(r_1=\frac{5760^{\circ}}{\pi m^{\circ}}\)
{
Now, let's subtract the 2 equations from each other. Let's see what happens. Unfortuntaely, I am no genius with LaTeX, so I could not line up the equal signs. Hopefully, you get the point...
\(\begin{eqnarray*} r_2=\frac{6120^{\circ}}{\pi m^{\circ}}\\ -\left(r_1=\frac{5760^{\circ}}{\pi m^{\circ}}\right)\\ \end{eqnarray*}\)
Let's subtract the two equations together. Let's start with the left hand side subtraction. \(r_2-r_1=1.5\), according to the given info. \(\frac{6120^{\circ}}{\pi m^{\circ}}-\frac{5760}{\pi m^{\circ}}=\frac{360}{\pi m^{\circ}}\). Knowing this, we can now solve for the central angle.
| \(1.5=\frac{360}{\pi m^{\circ}}\) | Multiply by \(\pi m^{\circ}\) on both sides. |
| \(1.5\pi m^{\circ}={360}\) | Divide by \(1.5\pi\) |
| \(m^{\circ}=\frac{360}{1.5\pi}\) | We can simplify the right hand side further, actually. First, let's convert 1.5 into a fraction. |
| \(\frac{360}{1.5\pi}=\frac{360}{\frac{3\pi}{2}}\) | In a fraction, \(\frac{a}{\frac{b}{c}}=\frac{a*c}{b}\). Let's apply it. |
| \(\frac{360}{\frac{3\pi}{2}}=\frac{360*2}{3\pi}\) | In the numerator and denominator, 3 can be factored out. |
| \(m^{\circ}=\frac{120*2}{\pi}=\frac{240}{\pi}\) | |
Now that I know the central angle in its exact form, I can now substitute it back into the arc length formula to ge the measure of the radii. Let's do that! FIrst, I'll solve for r1 first.
| \(l=\frac{m^{\circ}}{360^{\circ}}*2\pi r\) | As a reminder, this is the formula for arc length. Substitute the values we already know. |
| \(32=\frac{m^{\circ}}{360}*2\pi r_1\) | I have decided to leave out the measure of the angle for now, so the equation does not look like a monstrosity. Multiply both sides by 360. |
| \(11520=2\pi r_1m^{\circ}\) | Divide by 2 on both sides. |
| \(5760=\pi r_1m^{\circ}\) | Now, let's plug in m. |
| \(5760=\pi r_1\left(\frac{240}{\pi}\right)\) | Eliminate the pi's as they cancel out. |
| \(5760=240r_1\) | Divide by 240 on both sides. |
| \(r_1=\frac{5760}{240}=24units\) | I happen to know that 24^2=576, so this division was relatively easy for me. I will not forget the units, either! |
We don't have to do this same process for r2 luckily as \(r_1+1.5=r_2\). Therefore, \(r_2=24+1.5=25.5units\)
.