I've been thinking more about this question.
When the graph of a certain function f(x) is
shifted 2 units to the right
and stretched vertically by a factor of 2 (meaning that all y-coordinates are doubled), the resulting figure is identical to the original graph. Given that f(0)=0.1, what is f(10)?
From my previous answer I have:
| x | 0 | 2 | 4 | 6 | 8 | 10 |
| f(x) | 0.1 | 0.2 | 0.4 | 0.8 | 1.6 | 3.2 |
These points satisfy the equation
\(f(x)=0.1*2^{(n/2)}\)
I graphed this to check it worked properly. It did :)
https://www.desmos.com/calculator/ugcl3yupfo
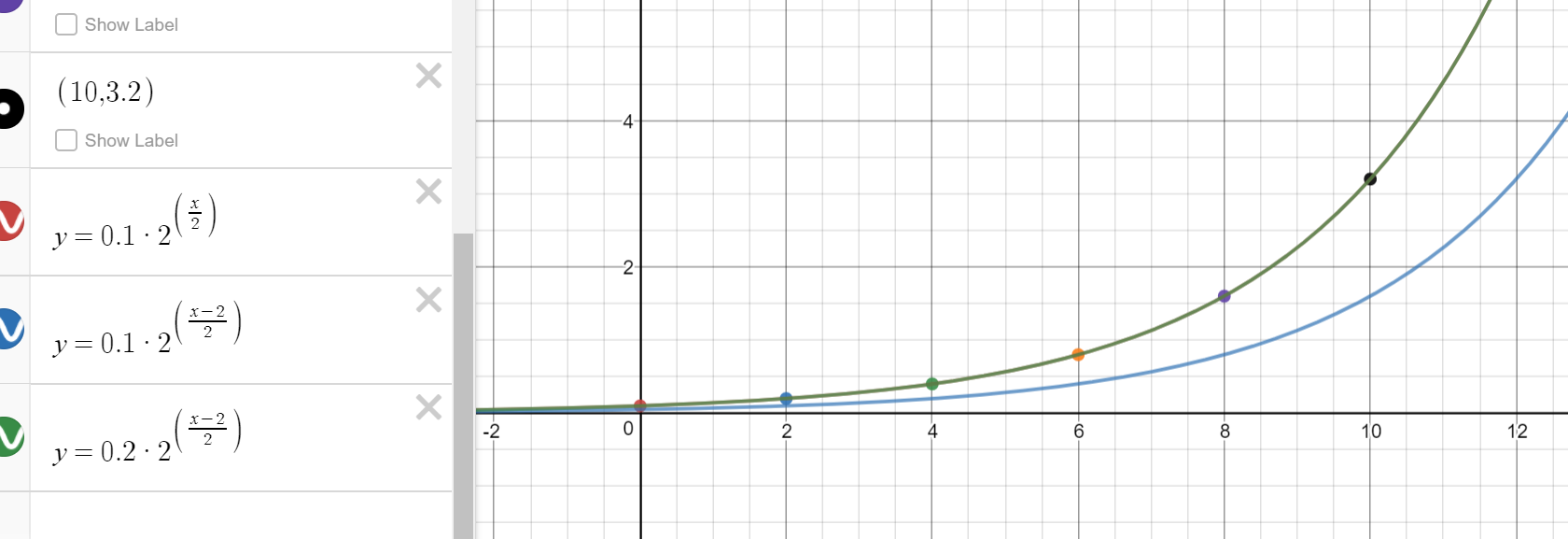
I am almost sure that if I think about it hard enough I could learn something more about transformations from this question ......
Is the equation \(\sqrt{\sqrt{34}}=\sqrt{c^2}\) in which you want solved? This is what I intepret it as. I will solve it:
| \(\sqrt{\sqrt{34}}=\sqrt{c^2}\) | Square both sides of the equation to get rid of one set of square roots. |
| \(\sqrt{34}=c^2\) | Take the square root of both sides. Of course, taking the square root results in a positive and negative answer. |
| \(c=\pm\sqrt{\sqrt{34}}\) | Now, let's simplify. \(\sqrt{\sqrt{34}}\)Note that \(\sqrt[n]{a}=a^{\frac{1}{n}}\). |
| \(\sqrt{\sqrt{34}}=(\sqrt{34})^{\frac{1}{2}}\) | Let's use the same principle as above. |
| \((\sqrt{34})^{\frac{1}{2}}=\left(34^{\frac{1}{2}}\right)^{\frac{1}{2}}\) | In the current situation we are in, we will use the rule that \(\left(a^b\right)^c=a^{b*c}\). |
| \(\left(34^{\frac{1}{2}}\right)^{\frac{1}{2}}=34^{\frac{1}{2}*\frac{1}{2}}=34^{\frac{1}{4}}\) | Yet again, we will use the inverse of \(\sqrt[n]{a}=a^{\frac{1}{n}}\) to simplify. |
| \(c=\pm\sqrt[4]{34}\approx\pm2.4147\) | |
Now, we must check that \(\pm\sqrt[4]{34}\) are valid solutions to this equation. I'll check them separately.
| \(\sqrt{\sqrt{34}}=\sqrt{c^2}\) | Plug in the value of \(\sqrt[4]{34}\) and check its validity. |
| \(\sqrt{\sqrt{34}}=\sqrt{\left(\sqrt[4]{34}\right)^2}\) | This may look complicated, but it can be simplified by realizing that\(\sqrt{a^2}=a\), assuming \(a\geq0\) |
| \(\sqrt{\sqrt{34}}=\sqrt[4]{34}\) | We already calculated earlier than the square root of the square root of a number has a square root index of 4. |
| \(\sqrt[4]{34}=\sqrt[4]{34}\) | |
Now, let's check the other answer.
| \(\sqrt{\sqrt{34}}=\sqrt{\left(-\sqrt[4]{34}\right)^2}\) | This time, we cannot use the rule we used before because \(-\sqrt[4]{34}<0\). Let's rewrite this as an exponent. |
| \(\sqrt{\sqrt{34}}=\sqrt{\left(-34^{\frac{1}{4}}\right)^2}\) | Let's use the exponent rule we have used before that states that \(\left(a^b\right)^c=a^{b*c}\). Note that squaring a number automatically makes a number positive, so that is why the negative sign disappears in the next step. |
| \(\left(-34^{\frac{1}{4}}\right)^2=34^{\frac{1}{4}*\frac{2}{1}}=34^{\frac{2}{4}}=34^{\frac{1}{2}}=\sqrt{34}\) | Reinsert this into the equation and compare. |
| \(\sqrt{\sqrt{34}}=\sqrt{\sqrt{34}}\) | This statement is true, as both sides are the same, so both values for c are solutions. |
Therefore, \(c=\pm\sqrt[4]{34}\)
.