All Answers 357307 Answers

Thanks Guest, if this is CPhill's answer it would have been nice if you had included the address of the original question/answer.

It is really nice that you have given CPhill the credit though :)

Thank you all, sir.

Why is that

Thanks SOOO much!!!

Be warned that the answer is  - $0.50 I tried 0.50 on accident. 

Looks like someone is a fan of Nauseated!

The balls are all the same so the only differenciating thing is how many balls are in each individual box.

The boxes can have

0,0,4       3 possibilities

0,1,3       6 possibilities

0,2,2       3 possibilities

1,1,2       3 possibilities

So that are 15 unique outcomes

If the boxes were distinguishable then your solution would be correct. In effect, this is distributing indistinguishable balls (k) into distinguishable boxes (N), forming a combination of size k, taken from a set of size n.

 $$\displaystyle \left( {\begin{array}{*{20}c} 4 \\3 \\ \end{array}} \right)\; = \; \dfrac{(4)!}{3!(4-3)!} \; = \;\hspace{5pt} \Text {4 \ ways} \\\$$

When both b***s and boxes are indistinguishable, empty boxes are forbidden, if they were allowed then they are distinguishable, and the above formula would apply.

The reason for this is the mathsgod said so. Mathsgod, please come and verify the veracity of this statement.

These types of questions are not intuitive. Consider your statement: “All the balls and all the boxes are identical . . .” Though it would seem so, this is not the same as indistinguishable in a mathematical sense.

If identical boxes are present at the same time then they are identifiable via their positions in space. Like many hypothetical math questions, it becomes difficult -- sometimes impossible-- to create a real situation where these concepts can be examined. Many math realities exist only in the mathematics and cannot exist in our normal space-time. Torricelli's trumpet is a classic example of this.

This question can exist in normal space but probably not with boxes. An approximation might be to place the boxes behind a frosted glass that distorts their size, shape and position in space. This approximation still falls short. To be true to the question, the boxes cannot exist until the b***s are placed in them. This is why it is a partition question. There are no empty partitions because the balls themselves make the partitions.

As complex as this may seem, it becomes more so when the balls are distinguishable. These are royal ball-busters. Sterling numbers of the second kind are used for these partitions. 

Expected value =

Amt spent * (probability of losing)  +  Jackpot * (probability of winning)  =

-3 * (99,999/100000) +   250,000* (1/100000)  ≈  -$0.50

CPhill Sep 1, 2017

This is easy! Just deflate the balls if they don't fit in the box when inflated!

Thank you so much!!!

3(4*1+5*7)  do multiplications inside the bracket first

3(4 + 35) =

3*(39) =117

thank you so much you explaned it well

2x^(5/3) + 64 = 0

2x^(5/3) = -64    divide both sides by 2

x^(5/3) =-32        Take (5/3)th root of both sides

Simplify the following:
(-32)^(1/(5/3))

Multiply the numerator of 1/(5/3) by the reciprocal of the denominator. 1/(5/3) = (1×3)/5:
(-32)^(3/5)

(-32)^(3/5) = ((-32)^3)^(1/5) = ((-1)^3×32^3)^(1/5) = ((-1)^3×2^15)^(1/5):
((-1)^3 2^15)^(1/5)

((-1)^3 2^15)^(1/5) = ((-1)^3)^(1/5) (2^15)^(1/5) = (-1)^(3/5)×2^(15/5) = (-1)^(3/5)×8:

x = 8×(-1)^(3/5)

Proof: 2 * [ 8*(-1)^(3/5)]^(5/3) =-64 + 64 =0

thank you so much

Here is a graphical approximation of the solutions (There are 2 solutions)

 x is approximately   0.63 or   20.06

Simplify.

x^2/ x-1/ 3x^2/ x+4.

There is no brackets so your meaning if not clear but this is the question that you have asked.

$Simplify\\ x^2/ x-1/ 3x^2/ x+4\\ =(x^2/ x)\quad- ((1/ 3)x^2)/ x)\quad+4\\ =x \quad - \quad \frac{1x^2}{3}\div x\quad +4\\ =x \quad - \quad \frac{1x^2}{3x}\quad +4\\ =x \quad - \quad \frac{x}{3}\quad +4\\ =\frac{2x}{3}+4\\ =\frac{2x+12}{3}$

Hey that was much easier to follow than mine, great job. 👍🏻

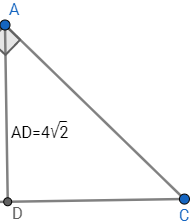
I know why the guest got this question incorrect. Let's assume that $m\angle ADC=90^{\circ}$, thus making it a right triangle. Let's make the assumption, too, that $AD=DC$, thus making it an isosceles triangle. 

However, there is a key word. That word would happen to be "altitude." An altitude is a perpendicular height that extends from a vertex to the opposite side. Notice how the height of this triangle does not do this. Therefore, the original diagram does not fit the original criteria. 

 3+4*(10-8) = do the brackets first

3  + 4 *(2)    =  Multiply 4 x 2

3  +  8        =    add 3 + 8

=11

Okay, so you take 3+4(10-8) and multiply 4 times 10 and 4 times -8. Now you have this equation…

3+40-32. So you add 40 and 3 together which equals 43, then subtract 32 and now you have your answer 11. 

3+4(10-8)=11😜

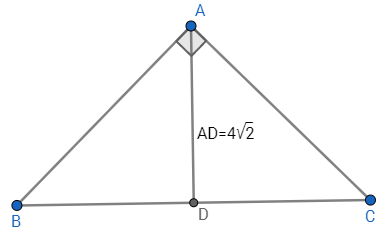
This is a sketch of the given info. $\overline{AD}$ is an altitude and $\overline{AC}\cong\overline{AB}$, and the triangle is right.

Because $\overline{AC}\cong\overline{AB}$ by the given info, the isosceles triangle theorem tells us that the angles opposite of their sides are congruent, so $\angle B\cong\angle C$. We can now figure out $m\angle B\quad\text{and}\quad m\angle C$.

Since an altitude always bisects the angle of an isosceles triangle, $m\angle CAD=\frac{1}{2}*90=45^{\circ}$. 

Since $m\angle CAD=m\angle C=45^{\circ}$, by the inverse of the isosceles triangle theorem, $AD=DC=4\sqrt{2}$

The entire base, however, is 2 times this length, so $BC=2*4\sqrt{2}=8\sqrt{2}$. The altitude is $4\sqrt{2}$. Now, let's use the area formula for a triangle.

5x - 17  =  -x + 7

Add  x  to both sides of the equation.

6x - 17  =  7

Add  17  to both sides of the equation.

6x  =  24

Divide both sides by  6 .

x  =  4

Check:  does   5(4) - 17  =  -4 + 7   ?

                                   3   =   3          Yep!

The length of $\overline{AC}$ can be found using the law of cosines. The law of cosines relates the remaining side by knowing two sides and its opposite included angle. I think this picture sums it up nicely. 

Knowing this information, we can now find the missing length.

this is an important problem. anyone else get the same answer?

is the answer for sure 8 square units? for sure?