All Answers 356785 Answers

...........

Six 6-sided dice are rolled. What is the probability that exactly two of the dice show a 1 and exactly two of the dice show a 2? Express your answer as a common fraction.

P(2 twos and 2 ones and the other two different ) +  P(2 sixes and 2 ones and 2 of some other number)

\( =\frac{6!}{2!2!}*(\frac{1}{6}*\frac{1}{6}*\frac{1}{6}*\frac{1}{6}*\frac{4}{6}*\frac{3}{6}) + \frac{6!}{2!2!2!}*(\frac{1}{6}*\frac{1}{6}*\frac{1}{6}*\frac{1}{6}*\frac{4}{6}*\frac{1}{6})\\ =180*\frac{12}{6^6} + 90*\frac{4}{6^6}\\ =\frac{2160}{6^6} + \frac{360}{6^6}\\ =\frac{2520}{46656}\\ =\frac{35}{648} \\\approx 0.054\)

I do not think this is correct, I think 2160 should be half the size at 1080.

BUT I do not know what I did wrong. Probablility is like that ... it's sneaky!!

----------------------------------------------------------------------------

Here is another way to look at it 

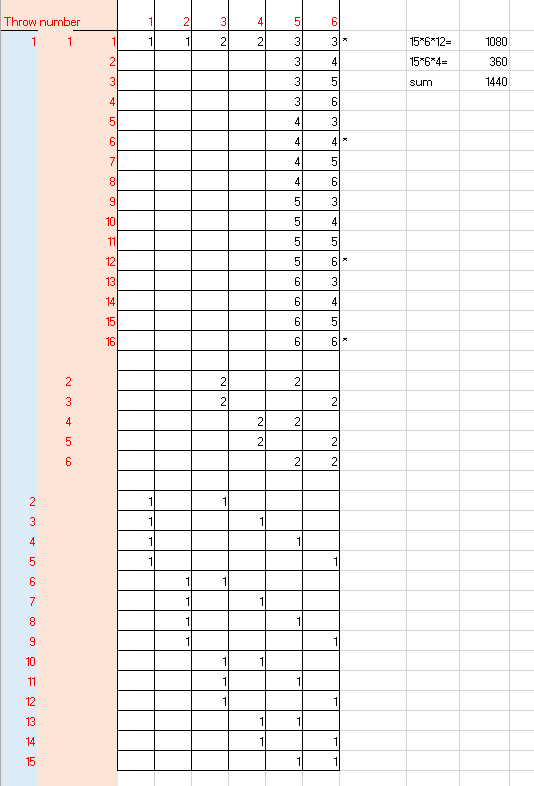
You have six squares an each square represents a number rolled.

There will be 6^6 = 46656  possible outcomes but I have to work out how many of those are favourable.

First there are 6C2 = 15 places where the 1s can go.

Now there are four spots left so

There are  4C2= 6 places where the 2s can go.

So far that is   15*6=90

Now there are 2 spots left.

If the the last two numbers are different then you can chose from 3,4,5, or 6

So there will be 4 choices for the next place and 3 fro the last place so that is    90*4*3 = 1080

If the the last two numbers are the same then you can chose from 3,4,5, or 6

So there will be 4 choices for the next place and 1 for the last place so that is    90*4*1 =360

So that is 1080+360 = 1440

So the probablility is \(\frac{1440}{6^6}=\frac{1440}{46656}=\frac{5}{162}\)

This is why I think that the second answer is correct. I counted the possibilities.

Alles Gute zum Geburtstag, Heureka

We have this

(-1)^2 + b(-1)  + c  = -11

(3)^2 + b(3)  + c   =  17

So we have

1 - b  +  c  =  -11

9 + 3b +  c  = 17

-b +  c  =  -12       multiply through by -1  =  b - c  = 12     (1)

3b +  c   = 8       (2)

Add (1)  and (2)

4b  =  20     divide both sides by 

b  = 5

And using (1)

5 - c  = 12    ⇒    c =  -7

We want to first solve this  for a

a(2) + 4  =  2(2)^2 - 3     simplify

2a + 4  =  8 - 3

2a + 4  =  5     subtract 4 from both sides

2a  = 1     divide both sides by 2

a  = 1/2

Here is the graph :  https://www.desmos.com/calculator/6oknzzh6sz

$1.50 - [30%x$1.50] =

$1.50 - [0.30x$1.50] =

$1.50 - $0.45 =$1.05 - New price of hot pretzel.

Since 23478 prime factors are = 2 * 3 * 7 * 13 * 43, and the first 4 factors are common to the polynomial f(x)=(2x+3)(7x+2)(13x+7)(x+13), therefore no matter what value x takes, the GCD of the polynomial and x will ALWAYS be = 2 x 3 x 7 x 13 = 546 !!.

Conversation between friend and me: 

So you can write f(x) = (x-p)(x-q)(x-r)(x-s)+5, which will satisfy the thing and then minimize it since everything is integer

oh yeah

but how to minimize it]

isnt the minimumn 5?

f(x)>5 though

Plug in x=t

ok

Basically minimize positive value of four different integers (t-whatever)

Value of product of four

 f(t) = (t-p)(t-q)(t-r)(t-s)+5>5, so   (t-p)(t-q)(t-r)(t-s)>0

?

 (t-p)(t-q)(t-r)(t-s) would be 1*2*3*4?

at minimum

Yeah so the product of the four t's need to be positive and distinct since p,q,r,s are different

so the answer wold be 24?

No

Wait

The product has to be positive but not each term

oh

And add 5

-1, 1, -2, 2 product=4, plus 5 is 9?

so it would be 9?

And the answer is 9

Thanks a lot!

THanks Melody!

This is the sum of an infinite geometric series:

Sum =F / [1 - R], where F = First term, R = Common Ratio

Sum = 12/ [1 - 1/2]

Sum = 12 / (1/2)

Sum = 12 x 2

Sum = 24 meters.

24 hours = 360 degrees, or:

1 hour = 15 degrees

7 1/3 x 15 =110 degrees. So:

110/360 =30.56% - spent working

1 - 0.3056 =69.44% - spent on non-work.

Really? Cool. I'm an 11th grader. :P

Thanks for catching my typo, guest.....!!!

Misplaced the decimal point =~1.85 lbs per person.

6.7 billion   =  6,700,000,000

302 million  =  302,000,000

So

6.700,000,000  / 302,000,000   ≈  22.19  lbs per year

So

22.19  / 12  ≈    1.85  lbs per person  per month

Yes, the 1st one: -5, 11

This seems tougher than it really is

The longest segment will be the hypotenuse of a right triangle with legs of 3 ft and  twice the radius =  8 ft....so....letting S be the segment length, we have that.....

S^2  =  3^2  +  8^2

S^2  =  9 +   64

S^2   = 73       take the positive square root of both sides

S  = √73 ft  ⇒  8.54 ft

would 2 be A??

1.   Not too bad,  NSS

√[ x + 10 ] - 9  = 7   add  9 to both sides

√ [ x + 10 ]   =  2        square both sides

x + 10  =  4       subtract 10 from both sides

x  = -6

2)

Solve for x:

4(3 - x)^4/3 - 5 = 59       add 5 to both sides

4(3 - x)^4/3 = 64            divide both sides by 4

(3 - x)^4/3 = 16              raise both sides to 3rd power

(x - 3)^4 = 4096

Taking 4^th roots gives 8 times the 4^th roots of unity:

x - 3 = -8 or x - 3 = -8 i or x - 3 = 8 i or x - 3 = 8

Add 3 to both sides:

x = -5 or x - 3 = -8 i or x - 3 = 8 i or x - 3 = 8

Add 3 to both sides:

x = -5 or x = 3 - 8 i or x - 3 = 8 i or x - 3 = 8

Add 3 to both sides:

x = -5 or x = 3 - 8 i or x = 3 + 8 i or x - 3 = 8

Add 3 to both sides:

x = -5 or x = 3 - 8 i or x = 3 + 8 i or x = 11 - Discard the imaginary solutions:

x = -5       and          x = 11

wow i do see oh my gosh you make it so simple more!! thank you so much

OK.....this looks a little daunting.....let's make it easier

Let     x /y  =  "a"

So     x^2 / y^2  =  (x /y)^2   =  "a^2"

Now.....we have someting that is a little more familiar....so....

4 (x^2/y^2)   - 36 (x/y)  + 81        becomes

4a^2  -  36a  + 81        let us guess that the factorization of this is

(2a - 9) (2a - 9)          verify for yourself that this is the correct factoring

(2a - 9)^2

But.....also ....notice that   

[ -(2a - 9) ]  [ - (2a - 9) ]    will also produce the same result  = [ - (2a - 9) ]^2

So......the square roots  are

±(2a - 9)       ....so....just back-substitute and we have

± [ 2(x/y) - 9 ]