All Answers 357330 Answers

Thank you CPhill!

That is interesing Heureka, I had not realised that there was enough infromation to draw the graph. :)

Suppose

$f(x)$

is a rational function such that  $3 f \left( \frac{1}{x} \right) + \frac{2f(x)}{x} = x^2$

for all $x \neq 0$. Find $f(-2)$.

$\begin{array}{|lrclcl|} \hline & 3f(\frac1x) + \frac2x f(x) &=& x^2 \\ & 3f(\frac1x) &=& x^2 - \frac2x f(x) \\ & f(\frac1x) &=& \frac{x^2}{3} - \frac{2}{3x} f(x) \qquad (1) \\ \\ \text{Set }x=\frac1x: & 3f(x) + 2x f(\frac1x) &=& \frac{1}{x^2} \\ & 2x f(\frac1x) &=& \frac{1}{x^2}-3f(x) \\ & f(\frac1x) &=& \frac{1}{2x^3}-\frac{3}{2x}f(x) \qquad (2) \\\\ \hline (1) = (2): & \frac{x^2}{3} - \frac{2}{3x} f(x) &=& \frac{1}{2x^3}-\frac{3}{2x}f(x) \\ & \frac{3}{2x}f(x) - \frac{2}{3x} f(x) &=& \frac{1}{2x^3} -\frac{x^2}{3} \\ & f(x)\left( \frac{3}{2x} - \frac{2}{3x} \right) &=& \frac{3-2x^5}{6x^3} \\ & f(x)\left( \frac{9x-4x}{6x^2} \right) &=& \frac{3-2x^5}{6x^3} \\ & f(x)\left( \frac{5x}{6x^2} \right) &=& \frac{3-2x^5}{6x^3} \\ & f(x)\left( \frac{5x}{1} \right) &=& \frac{3-2x^5}{x} \\\\ & \mathbf{f(x)} & \mathbf{=} & \mathbf{\dfrac{3-2x^5}{5x^2}} \\ \hline \end{array}$

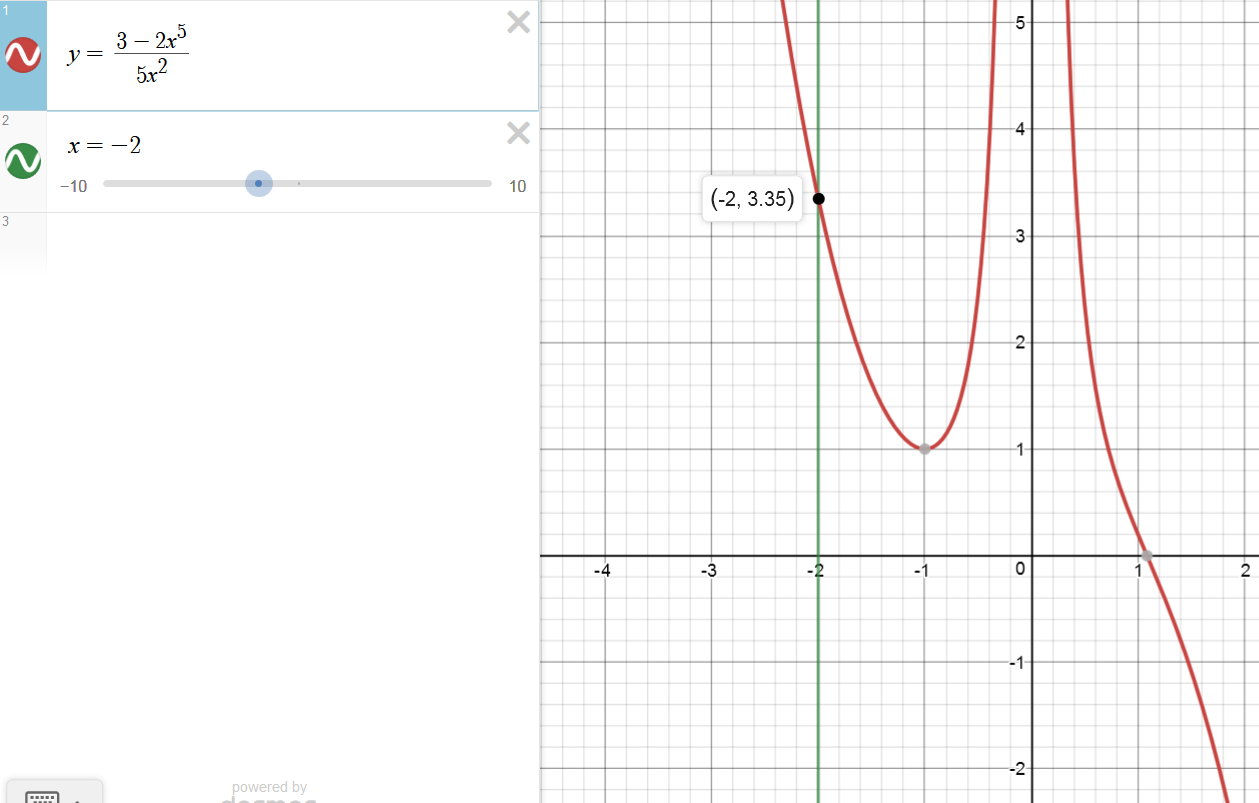
The rational function is  $f(x) = \dfrac{3-2x^5}{5x^2}$

$f(-2)=\ ?$

$\begin{array}{|rclcl|} \hline f(-2) &=& \frac{3-2(-2)^5}{5(-2)^2} \\ &=& \frac{3+2^6}{5\cdot 4} \\ &=& \frac{3+64}{20} \\ &=& \frac{67}{20} \\ \mathbf{f(-2)} & \mathbf{=} & \mathbf{3.35} \\ \hline \end{array}$

$\text{ $f(-2)$ is $3.35$ }$

graph:

Suppose f(x) is a rational function such that

$3 f \left( \frac{1}{x} \right) + \frac{2f(x)}{x} = x^2$

  for all $x\ne0$. Find f(-2).

We have

$3 f \left( \frac{1}{-2} \right) + \frac{2f(-2)}{-2} = (-2)^2\\ 3 f \left( \frac{1}{-2} \right) - f(-2) =4\qquad \qquad(1)\\ and\\ 3 f \left( \frac{1}{-1/2} \right) + \frac{2f(-1/2)}{-1/2} = (-1/2)^2\\ 3 f \left( -2 \right) -4f(\frac{-1}{2}) =\frac{1}{4}\\ -4f(\frac{-1}{2}) +3 f \left( -2 \right)=\frac{1}{4}\qquad\qquad (2)\\--------------\\~\\ \quad 3 f \left( \frac{1}{-2} \right) - f(-2) =4\qquad \qquad(1)\\ \quad 12f \left( \frac{1}{-2} \right) - 4f(-2) =16\qquad \qquad(1b)\\ -4f(\frac{-1}{2}) +3 f \left( -2 \right)=\frac{1}{4}\qquad\qquad (2)\\ -12f(\frac{-1}{2}) +9 f \left( -2 \right)=\frac{3}{4}\qquad\qquad (2b)\\~\\ (1b)+(2b)\\ 5f(-2)=16\frac{3}{4}\\ f(-2)=3\frac{7}{20}\\ $

The method is correct but you need to check for careless errors. 

16666.6666667

The area of the whole rectangle is (5 - 1)*0.25 = 1

You want the value of x=a such that (a - 1)*0.25 = 0.75

The period is the time for one complete cycle (2).

The amplitude is half the distance between peak and trough (10)

Frequency is 1/period cycles/second or 2pi/period radians per second.

What is the remainder when

$2001 \cdot 2002 \cdot 2003 \cdot 2004 \cdot 2005$

is divided by 19?

$\begin{array}{|rclcl|} \hline && 2001 \cdot 2002 \cdot 2003 \cdot 2004 \cdot 2005 \pmod{19} \\ &&&& 2001 \pmod{19} \\ &&&\equiv& {\color{red}6} \pmod{19} \\\\ &&&& 2002 \pmod{19} \\ &&&\equiv& {\color{red}7} \pmod{19} \\\\ &&&& 2003 \pmod{19} \\ &&&\equiv& {\color{red}8} \pmod{19} \\\\ &&&& 2004 \pmod{19} \\ &&&\equiv& {\color{red}9} \pmod{19} \\\\ &&&& 2005 \pmod{19} \\ &&&\equiv& {\color{red}10} \pmod{19} \\\\ &\equiv& 6 \cdot 7 \cdot 8 \cdot 9 \cdot 10 \pmod{19} \\ &\equiv& 30240 \pmod{19} \\ &\equiv& {\color{red}11} \pmod{19} \\ \hline \end{array}$

The remainder is 11

I'm the challenger, I post questions every week!

Week 1:

Find the units digit of 3^17*7^23?

$3^{17} * 7 ^{23} \pmod{10} = \ ?$

$\begin{array}{|rclcl|} \hline && 3^{17} * 7 ^{23} \pmod{10} \\ &\equiv& (3^2)^{8}*3^1*(7^2)*7^1 \pmod{10} \\\\ &&&& 3^2 \pmod{10} \\ &&&\equiv& 9 \pmod{10} \\ &&&\equiv& 9-10 \pmod{10} \\ &&&\equiv& {\color{red}-1} \pmod{10} \\\\ &&&& 7^2 \pmod{10} \\ &&&\equiv& 49 \pmod{10} \\ &&&\equiv& 9 \pmod{10} \\ &&&\equiv& 9-10 \pmod{10} \\ &&&\equiv& {\color{red}-1} \pmod{10} \\\\ &\equiv& ({\color{red}-1})^{8}*3^1*({\color{red}-1})*7^1 \pmod{10} \\ &\equiv& 3 *(-7) \pmod{10} \\ &\equiv& -21 \pmod{10} \\ &\equiv& -1 \pmod{10} \\ &\equiv& -1+10 \pmod{10} \\ &\equiv& {\color{red}9} \pmod{10} \\ \hline \end{array}$

[Time - 4.6]  / 1.1   =  -1.2  multiply both sides by 1.1

Time - 4.6  =  -1.32      add 4.6 to both sides

Time  =  3.28  hrs

If  f(3)  = 5   and    f(3x)  = f(x) + 2, then .....

f(3x)  = f(3) + 2     implies that x  = 3

So

f(3 * 3)  = f(3) + 2

f(9)  =  5 + 2

f(9)  = 7

And

f(3x)  = f(9) + 2   implies that  x  = 9...so.....

f(3*9) = f(9) + 2

f(27)  = 9

And

f(3x)  = f(27) + 2   implies that x  = 27

f(3 * 27)  = f(27) + 2

f(81)  = 9 + 2

f(81) = 11

And   (81, 11)  is on the original graph  .....so  (11, 81)  is on the inverse

So

f^-1(11)  =  81

LOL!!!!....I didn't see that second one...see my added answer [ in red ]  ....

We are looking for the z score that corresponds with [ 1 - .70]   =  .30.....the closest value [per table]  is about -.52

So...we are trying to solve this

[ x  -15  ]  / 5.2  =  -.52       multiply both sides by 5.

 x - 15  =  -2.704  add 15 to both sides

x  = 12.296  = 12.3 years of age

I didnt know there was four lol, do u by chance know the last one?

m minor arc BCD   =  2  (angle A)

                                                                      Inscribed Angle Theorem

2m (angle A)  + 2 m (angle C)  = 360°

                                                                        Division Property of Equality

We have

[ 90  - 100 ]  / 25  =

-10 / 25  =

- 2 / 5  = 

- .4

The   table value for this z score  is  .3446

So

.3446  ( 400)  ≈  138  people

P ( 1 < X  < 5)  =

P(2) + P(3) + P(4)  =

0.07  + 0.22  + 0.22  =

0.51

We have

[ Observed value  - Mean Value  ] / Standard Deviation

[259 - 239]  / 25  =

20  / 25   =   4/ 5  =  .8  

S =[3/206] / [1 - 3/103]

S =[3/206] x [103/100]

S = 309 /20,600

S = 3 / 200

S = 0.015

Thank you sm!!

When the angle measure in given in radians, the formula for arc length is the following:

$\text{Arc length}=r\theta$

r = length of radius

$\theta =$ measure of angle, in radians

Let's use this formula, then!

We know  the oppoite side and the adjacent side....the inverse tangent is what we need

arctan ( 26/53)  = 26.1°

Arc  length, S,  is

S = r * theta (in radians)

S  =  21 5/8  *  ( 5 pi / 6)   =   [ 173/8 * 5 /6  * 3.14 ] =   56.59   yds

x^2   - y^2  = 1

(r cos  θ)^2  - (r sin  θ)^2  = 1

r^2 cos^2  θ - r^2 sin^2  θ   =  1

r^2 ( cos^2  θ  - sin^2  θ)  = 1

r^2  (cos 2 θ)  = 1 

x^2  + y^2   = 25

r^2  = 25

r  = 5