All Answers 357301 Answers

23^7 = 1/23^-7       Yes...when you move exponents up or down in a fraction the sign changes.

12^(-3)  =   1 /(12^3)        12^(-3) * 12^2 = 12^(-3+2) = 12^-1 = 1/12      or(12^(-1) )

4x = x (1+.02)^t           x can be any amount, so we'll leave it out.   I per period = 8/4 = .02% per quarter

      How many quarters? (t)

4 = (1.02)^t

log4/log1.02  = t  = 70   QUARTERS = 17.5 years  

As I recall, the chromosomes are not visible during interphase....the chromosome material is busy working and is not concentrated into chromosomes..... the cell is growing and gathering/building all the things it needs to reproduce and split later in telophase

IPMAT....the acronym for the phases   interphase   Prophase metaphase anaphase teliophase

Here is a light review:

https://quizlet.com/35367877/the-5-phases-of-the-cell-cycle-ipmat-flash-cards/

PLEASE, post questions only ONE TIME!  Thnx,

56%  x  1050 = 56/100 x 1050 =  .56 x 1050 = 588 boys

So first you divide 2 by both sides. So 2x/2 would be just be your variable alone.  Then 10/2 would be 5.  So your answer is x=5. 

The derivative is the gradient of the tangent to the curve at any given point.

Hi Alan,

How did you work out that  b must be greater or equal to 2-2a  ?

As long as b >= 2 - 2a the equation has at least one real root.  the line b = 2 - 2a is a straight line going from b = 2 when a = 0, to b = 0 when a = 1.  Hence the area of b >= 2 - 2a is a triangle of base 1 and height 2; i.e. the area is (1/2)*1*2 = 1.

All the positive integers greater than 1 are arranged in five columns (A, B, C, D, E) as shown.

Continuing the pattern, in what column will the integer 800 be written?

We rearrange:

$\small{ \begin{array}{|cccc|cccc|cccc|cccc|cccc|c|} \hline B&C&D&E& D&C&B&A& B&C&D&E& D&C&B&A& B&C&D&E& \ldots\\ \hline 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 &10 & 11 & 12 & 13 &14 & 15 & 16 & 17 &18 & 19 & 20 & 21 & \ldots \\ \hline \end{array} }$

$\begin{array}{|r|r!c|c|c|c|l|} \hline \text{Position} ~&(& 1 & 2 & 3 & 4\text{ or }0& ) \\ \hline \text{Row odd} ~&(& B & C & D & E &) \\ \text{Row even} ~&(& D & C & B & A &) \\ \hline \end{array}$

Formula:

$\begin{array}{|rcll|} \hline \text{Row} &=& 1 + \left\lfloor \dfrac{n-2}{4} \right\rfloor \quad & \quad \left\lfloor\ldots \right\rfloor \text{Function floor or Integerpart} \\\\ \text{Position} &=& (n-1) \pmod{4} \quad & \quad \text{If the position is zero, so the position is 4}\\ \hline \end{array}$

$\text{Row} =\ ?, ~n = 800:$

$\begin{array}{|rcll|} \hline \text{Row} &=& 1 + \left\lfloor \dfrac{800-2}{4} \right\rfloor \\ &=& 1 + \left\lfloor \dfrac{798}{4} \right\rfloor \\ &=& 1 + \left\lfloor 199.5 \right\rfloor \\ &=& 1 + 199 \\ &=& 200 \quad & \quad \text{the row is even!} \\ \hline \end{array}$

The number 800 is in row = 200. And the row is an even number.

$\text{Position} =\ ?, ~n = 800:$

$\begin{array}{|rcll|} \hline \text{Position} &=& (800-1) \pmod{4} \\ &=& 799 \pmod{4} \\ &=& 3 \\ \hline \end{array}$

$\text{Column} =\ ?, ~\text{Row is even}:$

$\begin{array}{|rcll|} \hline \hline \text{Position} ~&(& 1 & 2 & \color{red}3 & 4\text{ or }0& ) \\ \hline \text{Row even} ~&(& D & C & \color{red}B & A &) \\ \hline \end{array}$

The integer 800 will be written in column B

In that case you'd need a period after English which is probably more correct anyway.

cool but the speed of slopex.net might is too fast for me

th 5 prob 5

The diagram shows a calculator screen on which the parabolas y=1/4(x-3)(x-8) and y=1/2(x+1)(x-3) have been graphed. The window setting consists of two inequalities, A is less than or equal to X is less than or equal to B and C is less than or equal to Y is less than or equal to D. What are the values of a, b, c, and d? Explain your reasoning, please!!

$\mathbf{y=\dfrac14(x-3)(x-8)}\\ \begin{array}{|lrcll|} \hline x =8 ~\Rightarrow~ y = 0 ~\Rightarrow~ b=8 \\ \hline \end{array}$

$\begin{array}{|lrcll|} \hline x =0 ~\Rightarrow~ &y&=&\dfrac14(-3)(-8) \\ & y&=&\dfrac14\cdot 3 \cdot 8 \\ & y &=& 6 ~\Rightarrow~ d=6 \\ \hline \end{array}$

$\mathbf{y=\dfrac12(x+1)(x-3)}\\ \begin{array}{|lrcll|} \hline x_{\text{vertex}} &=& \dfrac{-1+3}{2} \\ &=& 1 \\\\ y_{\text{vertex}} &=&\dfrac12(1+1)(1-3) \\ &=&-2 ~\Rightarrow~ c=-2 \\ \hline \end{array}$

$\begin{array}{|lrcll|} \hline y = 6 ~\Rightarrow~ &6& =&\dfrac12(x+1)(x-3) \\ &12&=& (x+1)(x-3) \\ & x^2-2x-3 &=& 12 \\ & x^2-2x-15 &=& 0 \\ & x &=& \dfrac{2\pm \sqrt{4-4\cdot (-15)}}{2} \\ & x &=& \dfrac{2\pm \sqrt{64}}{2} \\ & x &=& \dfrac{2\pm 8}{2} \\\\ & x &=& \dfrac{2+ 8}{2} \\ & x &=& 5 \\\\ & x &=& \dfrac{2- 8}{2} \\ & x &=& -3 ~\Rightarrow~ a=-3 \\ \hline \end{array}$

$-3 \le x \le 8 \\ -2 \le y \le 6$

Thanks!

$\frac{(cot\alpha cot\beta -1)}{(cot\alpha +cot\beta )}\\ =\frac{cos\alpha cos\beta-sin\alpha sin\beta}{sin\alpha sin\beta}\div \left(\frac{cos\alpha}{sin\alpha}+\frac{cos\beta}{sin\beta}\right)\\ =\frac{cos\alpha cos\beta-sin\alpha sin\beta}{sin\alpha sin\beta}\div \frac{2cos\alpha sin\beta}{sin\alpha sin\beta}\\ =\frac{cos\alpha cos\beta-sin\alpha sin\beta}{2cos\alpha sin\beta}\\ =\frac{cos\alpha cos\beta-sin\alpha sin\beta}{2cos\alpha sin\beta}\\ =\frac{cos(\alpha+\beta)}{sin(\alpha+\beta)}\\ =cot(\alpha+\beta)$

Oof, I got them wrong 

Could you please edit your question to get rid of all the irrelevant $ signs.

Then it will be easier to read and someone might attempt an answer.

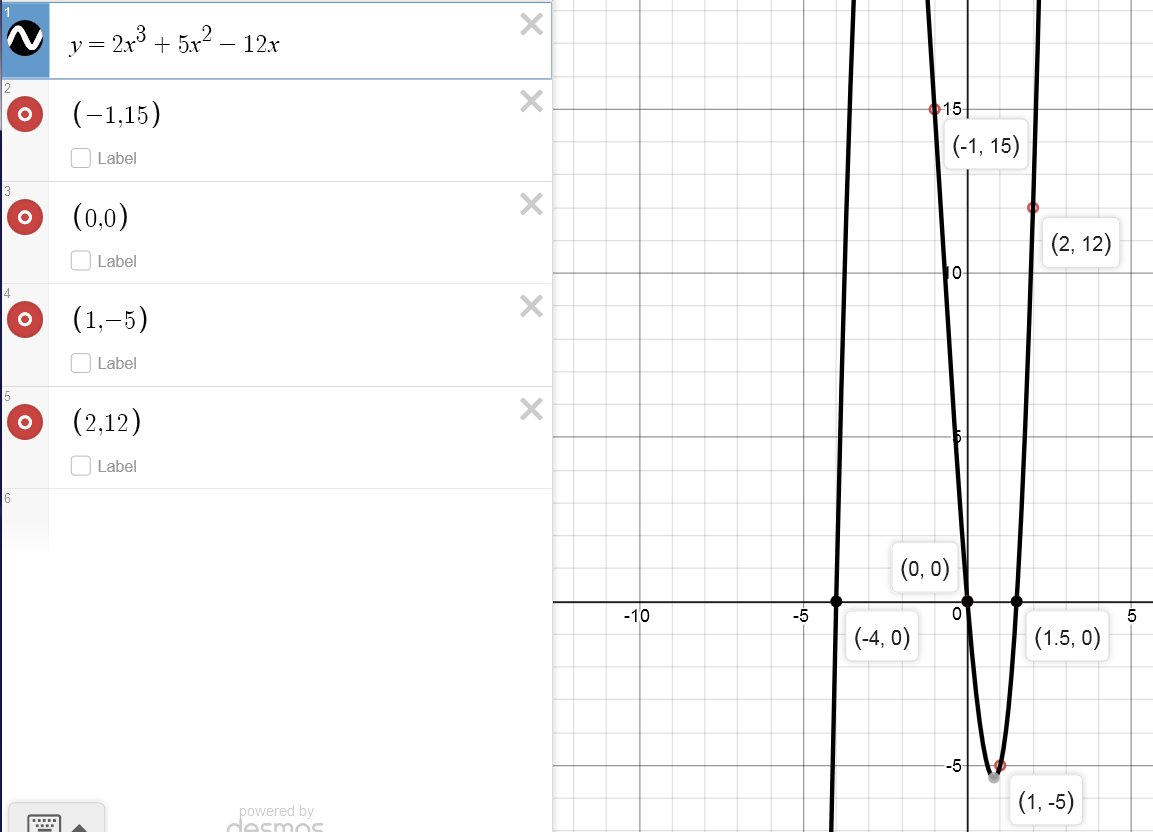
The polynomial f(x) has degree 3. If f(-1) = 15, f(0) = 0, f(1) = -5, and f(2) = 12,

 then what are the x-intercepts of the graph of f?

$\boxed{f(x) =ax^3+bx^2+cx+d}$ degree 3

$\begin{array}{|lrcll|} \hline f(0) = 0: & f(0) = 0 &=& a\cdot 0^3+ b\cdot 0^2+ c\cdot 0 +d \\ & 0 &=& d \\ & \mathbf {d }& \mathbf{=}& \mathbf{0} \\ \hline \end{array}$

So  $\boxed{f(x) =ax^3+bx^2+cx}$

$\begin{array}{|lrcll|} \hline f(1) = -5: & f(1) = -5 &=& a\cdot 1^3+ b\cdot 1^2+ c\cdot 1 \\ & -5 &=& a + b + c \\ & \mathbf {a + b + c }& \mathbf{=}& \mathbf{-5} \qquad (1) \\ \hline \end{array}$

$\begin{array}{|lrcll|} \hline f(-1) = 15: & f(-1) = 15 &=& a\cdot (-1)^3+ b\cdot (-1)^2+ c\cdot (-1) \\ & 15 &=& -a + b - c \\ & \mathbf {-a + b - c }& \mathbf{=}& \mathbf{15}\qquad (2) \\ \hline \end{array}$

$\mathbf{(1)+(2):}$

$\begin{array}{|lrcll|} \hline (1) & \mathbf {a + b + c }& \mathbf{=}& \mathbf{-5} \\ (2) & \mathbf {-a + b - c }& \mathbf{=}& \mathbf{15} \\ \hline (1)+(2): & 2b &=& -5+15 \\ & 2b &=& 10 \\ & \mathbf {b }& \mathbf{=}& \mathbf{5} \\ \hline (1) : & a+b+c &=& -5 \quad | \quad b=5 \\ & a+5+c &=& -5 \\ & \mathbf {a+c} &\mathbf {=}& \mathbf {-10} \qquad (3) \\ \hline \end{array}$

$\begin{array}{|lrcll|} \hline f(2) = 12: & f(2) = 12&=& a\cdot (2)^3+ b\cdot (2)^2+ c\cdot (2) \\ & 12 &=& 8a + 4b +2c \quad | \quad b=5 \\ & 12 &=& 8a + 4\cdot 5 +2c \\ & 12 &=& 8a + 20 +2c \\ & 8a + 2c &=& 12-20 \\ & 8a + 2c &=& -8 \quad & | \quad :2 \\ & \mathbf {4a + c}& \mathbf{=}& \mathbf{-4}\qquad (4) \\ \hline \end{array}$

$\mathbf{(4)-(3):}$

$\begin{array}{|lrcll|} \hline (4) & \mathbf {4a + c}& \mathbf{=}& \mathbf{-4} \\ (3) & \mathbf {a+c} &\mathbf {=}& \mathbf {-10}\\ \hline (4)-(3): & 3a &=& -4+-(-10)\\ & 3a &=& 6 \\ & \mathbf {a }& \mathbf{=}& \mathbf{2} \\ \hline (3) : & a+c &=& -10 \quad | \quad a=2 \\ & 2+c &=& -10 \\ & \mathbf {c} &\mathbf {=}& \mathbf {-12} \\ \hline \end{array}$

$\mathbf{\text{The $x$-intercepts of the graph of $~\boxed{f(x)=2x^3+5x^2-12x}$:}}$

$\begin{array}{|rcll|} \hline 2x^3+5x^2-12x &=& 0 \\ x\cdot (2x^2+5x-12) &=& 0 \\ \hline \mathbf{x_1} & \mathbf{=}& \mathbf{ 0 } \\ \hline 2x^2+5x-12 &=& 0 \\ x &=& \dfrac{-5\pm \sqrt{25-4\cdot 2 \cdot (-12)} } {2\cdot 2} \\\\ x &=& \dfrac{-5\pm \sqrt{121} } {4} \\\\ x &=& \dfrac{-5\pm 11 } {4} \\\\ x_2 &=& \dfrac{-5+ 11 } {4} \\ \mathbf{x_2} & \mathbf{=}& \mathbf{ \dfrac32 } \\\\ x_3 &=& \dfrac{-5- 11 } {4} \\ \mathbf{x_3} & \mathbf{=}& \mathbf{ -4 } \\ \hline \end{array}$

The x-intercepts of the graph of f(x) are $0,\dfrac32, -4$

Thanks, heureka!

- PM