Here's a diagram :
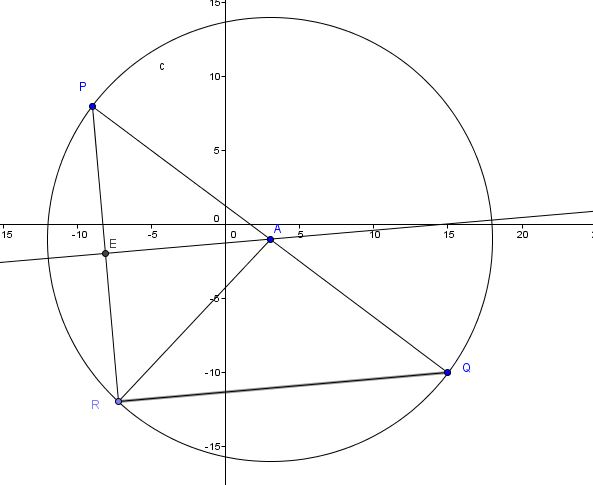
c) If we draw a radius bisecting chord PR.....it will meet PR at right angles......let E be the intersection of this radial line and the chord
Triangle AEP is right with AP = 15, PE = 10
So.....AE is the distance from A to PR.......and by the Pythagorean Theorem
AE = √[ AP^2 - AE^2] = √ [ 15^2 - 10^2 ] = √ [ 225 - 100] = √125 = 5√5 units
d) Angle APR = angle APE
And we can find the measure of angle APE as
cos APE = PE / AP = 10 / 15 = 2 /3
So
arccos (2/3) = 48.189°
And angle APR = angle QPR......but angle RAQ = twice the measure of angle APE = 2 * 48.189 ≈ 96.4°
But...in triangle RAQ, AR = AQ.....so angle ARQ = angle AQR
Angle ARQ can be found as [ 180 - angle RAQ] / 2 = [ 180 - 96.4 ] / 2 ≈ 41.8°


