Here is a video to explaing angle of depression and angle of elevation to you.
It is good. You should watch it.
https://www.youtube.com/watch?v=Sja5rEqmpa4
And here is your diagram. You should work out the hight the plane is above the tower first.
You do not need any angles or trig for that :)
Think about what I have already given you and try and answer the question yourself.
You can always add another response to ask more questions if you get stuck.
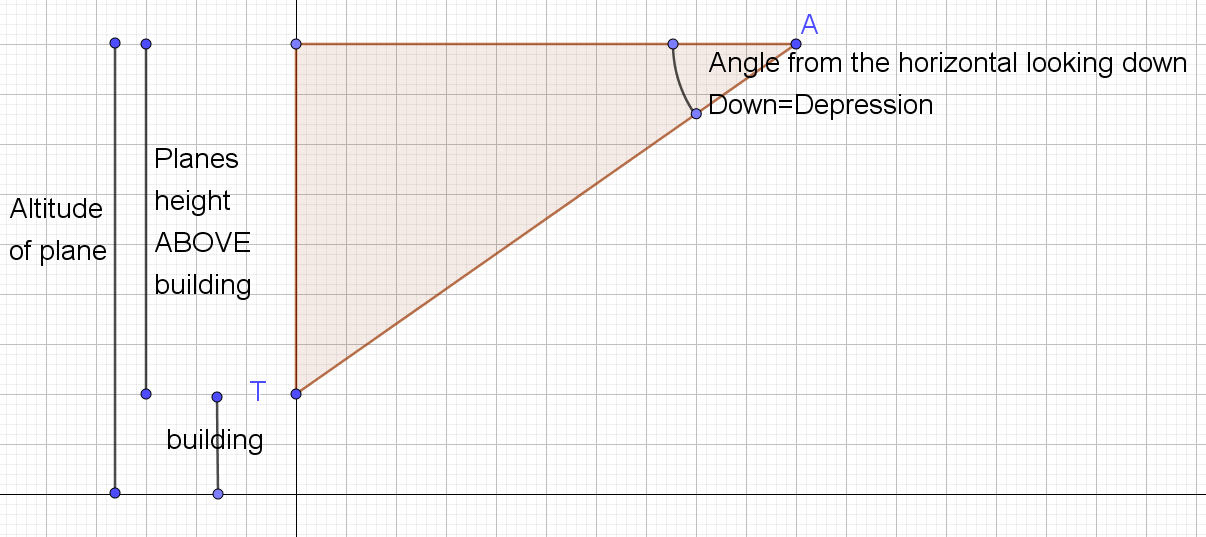
I think a diagram would allow you to visualize the problem.
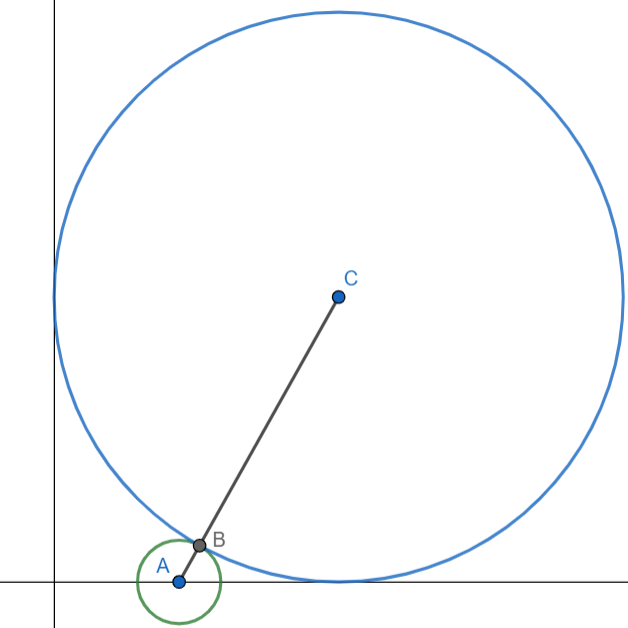
Let r equal the length of the radius of circle C.
The restrictions on circle C are such that the center is equidistant from both axes and lies in the first quadrant of the coordinate plane. I have defined the length of the radius to be r, so the center is r units away from both axes; therefore, the coordinates of the center are \((r,r)\) .
I am going to represent the distance from both centers in two different ways.
Since circle C and circle A are externally tangent, they intersect at only one common point. \(l_{\overline{BC}}=r\) because that segment is another radius, and all radii have the same length. \(l_{\overline{BA}}=1\) because the radius of circle A is given as 1.
\(l_{\overline{AC}}=l_{\overline{BC}}+l_{\overline{BA}}=r+1\)
\(r+1\) is the first way to represent the distance between the center of both circles. The second way requires the distance formula.
| \(\text{distance between }(r,r)\text{ and }(3,0);\\ d_{\overline{AC}}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\) | (3,0) is the coordinate of the center of the circle A. (r,r) is the coordinate of the center of the circle C. |
| \(d_{\overline{AC}}=\sqrt{(r-3)^2+r^2}\) | This is the second way to represent the distance between the center of both circles. |
\(r+1\text{ and }\sqrt{(r-3)^2+r^2}\) represent the same idea: the distance between the center of both circles. This means that they are equal.
| \(\sqrt{(r-3)^2+r^2}=r+1\) | Before beginning to solve this problem, we must compute the domain restriction on this equality since a square root is present. |
| \((r-3)^2+r^2\geq 0\\ r^2-6r+9+r^2\geq 0\\ 2r^2-6r+9\geq 0\) | Expand this inequality fully on the left side. |
| \(a=2, b=-6, c=9\\ \Delta=b^2-4ac\\ \Delta=(-6)^2-4*2*9\\ \Delta=-36\\ ∴ \text{No restriction in domain}\\ D:(-\infty,\infty) \) | Delta represents the discriminant of this quadratic inequality. This quadratic has a positive leading coefficient, so the corresponding parabola faces upward in the coordinate plane. \(\Delta<0\), which means that this parabola never intersects the x-axis. The only way for both conditions to be true is that the parabola is forever above the x-axis, so the function will always output a value greater than zero. |
| \(\sqrt{(r-3)^2+r^2}=r+1\) | Solve for r by using algebraic manipulation. |
| \((r-3)^2+r^2=(r+1)^2\\ (r-3)^2+r^2-(r+1)^2=0\\ r^2-6r+9+r^2-(r^2+2r+1)=0\\ 2r^2-6r+9-r^2-2r-1=0\\ r^2-8r+8=0\) | Square both sides to eliminate the radical, bring all terms to the left-hand side of the equation, and simplify the left-hand side of the equation completely. This quadratic is not factorable, so we will have to resort to other methods to find the solutions. |
| \(a=1, b=-8, c=8\\ r_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ r_{1,2}=\frac{-(-8)\pm\sqrt{(-8)^2-4*1*8}}{2*1}\\ r_{1,2}=\frac{8\pm\sqrt{32}}{2}\\ r_{1,2}=\frac{8\pm4\sqrt{2}}{2}\\ r_{1,2}=4\pm2\sqrt{2}\\ r_1=4+2\sqrt{2}\text{ or }r_2=4-2\sqrt{2}\) | Use the quadratic formula to determine both solutions. Both solutions are positive, so they are both valid for the context of this problem. |
| \(r_1+r_2\\ 4+2\sqrt{2}+4-2\sqrt{2}\\ 8\) | The sum of all possible radii is 8. |