16.
In ABC with a right angle at C,
point D lies in the interior of AB and
point E lies in the interior of BC so that
AC=CD, DE=EB, and the ratio AC:DE = 4:3.
What is the ratio AD:DB?
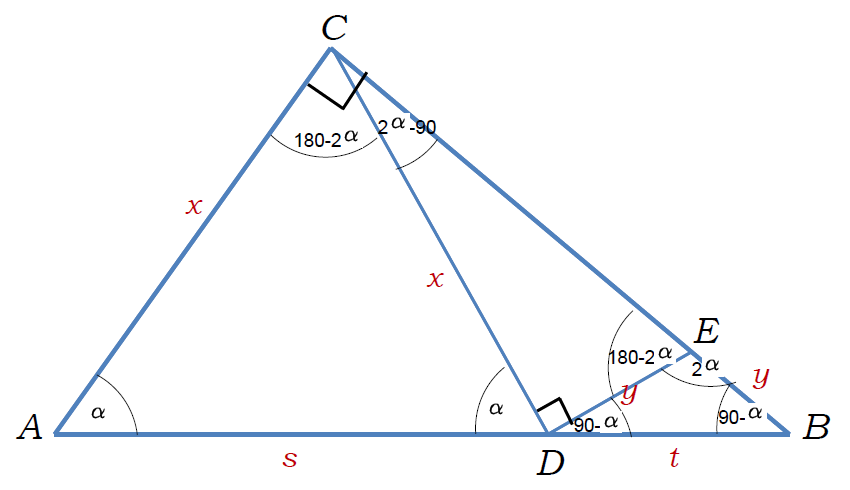
\(\text{Let $\overline{AC} = \overline{CD} = {\color{red}x} $ } \\ \text{Let $\overline{DE} = \overline{EB} = {\color{red}y} $ } \\ \text{Let $\overline{AD} = {\color{red}s} $ } \\ \text{Let $\overline{DB} = {\color{red}t} $ } \)
\(\text{Let $\angle{CAD} = \angle{ADC} = \alpha $ } \\ \text{Let $\angle{ABC} = \angle{EDB} = 90^{\circ}-\alpha $ } \\ \text{Let $\angle{DCA} = 180^{\circ}-2\alpha $ } \\ \text{Let $\angle{ECD} = 90^{\circ}-\angle{DCA} = 90^{\circ} -(180^{\circ}-2\alpha) = 2\alpha-90^{\circ} $ } \\ \text{Let $\angle{BED} = 180^{\circ}-2(90^{\circ}-\alpha)=2\alpha $ } \\ \text{Let $\angle{DEC} = 180^{\circ}-\angle{BED}=180^{\circ}-2\alpha $ } \)
\(\begin{array}{|rcll|} \hline \angle{CDE} &=& 180^{\circ}- \angle{ECD}-\angle{DEC} \\ &=& 180^{\circ}-(2\alpha-90^{\circ})- (180^{\circ}-2\alpha ) \\ &\mathbf{=}& \mathbf{90^{\circ} \ !} \\ \hline \end{array} \)
\(\mathbf{\text{$\cos$-rule in $\triangle ACD$}} \)
\(\begin{array}{|rcll|} \hline x^2 &=& x^2+s^2-2xs\cos(\alpha) \\ 2xs\cos(\alpha) &=& s^2 \\ \mathbf{2x\cos(\alpha)} & \mathbf{=} & \mathbf{s} \quad & (1) \\ \hline \end{array}\)
\(\mathbf{\text{$\cos$-rule in $\triangle DEB$}}\)
\(\begin{array}{|rcll|} \hline y^2 &=& y^2+t^2-2yt\cos(90^{\circ}-\alpha) \\ 2yt\sin(\alpha) &=& t^2 \\ \mathbf{2y\sin(\alpha)} & \mathbf{=} & \mathbf{t} \quad & (2) \\ \hline \end{array}\)
\(\begin{array}{|lrcll|} \hline \dfrac{(1)}{(2)}: & \dfrac{ 2x\cos(\alpha) } {2y\sin(\alpha) } &=& \dfrac{ s }{t} \\ \\ & \dfrac{x}{y} \cdot \dfrac{ \cos(\alpha) } {\sin(\alpha) } &=& \dfrac{ s }{t} \\ \\ & \mathbf{ \dfrac{x}{y} \cdot \dfrac{ 1 } {\tan(\alpha) }} & \mathbf{=} & \mathbf{\dfrac{ s }{t}} \quad & (3) \\ \hline \end{array}\)
\(\mathbf{\text{In the right-angled $\triangle DCE$}} \\ \mathbf{ \tan(\alpha) =\ ?}\)
\(\begin{array}{|rcll|} \hline \tan(180^{\circ}-2\alpha) &=& \dfrac{x}{y} \\\\ -\tan(2\alpha) &=& \dfrac{4}{3} \quad | \quad \text{Formula:} \ \boxed{ \tan(2\alpha)=\dfrac{2\tan{\alpha}}{1-\tan^2(\alpha)} } \\\\ \dfrac{-2\tan{\alpha}}{1-\tan^2(\alpha)} &=& \dfrac{4}{3} \\\\ \dfrac{2\tan{\alpha}}{\tan^2(\alpha)-1} &=& \dfrac{4}{3} \\\\ \dfrac{ \tan{\alpha}}{\tan^2(\alpha)-1} &=& \dfrac{2}{3} \\\\ 3\tan{\alpha} &=& 2(\tan^2(\alpha)-1) \\ 3\tan{\alpha} &=& 2\tan^2(\alpha)-2 \\ 2\tan^2(\alpha)-3\tan(\alpha)-2 &=& 0 \\\\ \tan(\alpha)&=& \dfrac{3\pm \sqrt{9-2\cdot4\cdot(-2)}} {2\cdot 2} \\\\ \tan(\alpha)&=& \dfrac{3\pm \sqrt{25}} {4} \\\\ \tan(\alpha)&=& \dfrac{3\pm 5} {4} \\\\ \tan(\alpha)&=& \dfrac{3 {\color{red}+} 5} {4} \quad | \quad \tan(\alpha) > 0\ ! \\\\ \tan(\alpha)&=& \dfrac{8} {4} \\ \mathbf{ \tan(\alpha) }& \mathbf{=} & \mathbf{2} \\ \hline \end{array}\)
\(\begin{array}{|rcll|} \hline \mathbf{ \dfrac{x}{y} \cdot \dfrac{ 1 } {\tan(\alpha) }} & \mathbf{=} & \mathbf{\dfrac{ s }{t}} \quad | \quad \mathbf{\tan(\alpha)=2},\ \quad \dfrac{x}{y}=\dfrac{4}{3} \\\\ \dfrac{4}{3} \cdot \dfrac{1} {2} & = & \dfrac{ s }{t} \\\\ \dfrac{4}{6} & = & \dfrac{ s }{t} \\\\ \dfrac{2}{3} & = & \dfrac{ s }{t} \\\\ \mathbf{\dfrac{ s }{t}} &\mathbf{=}& \mathbf{\dfrac{2}{3}} \\ \hline \end{array} \)
\((A) \ 2:3\)
