Transpose the formula for ‘A’ and find the value of A when
k1 = k2 = 0.2
k3 = 0.5
x1 = 40 x 10-3
x2 = 125 x 10-3
x3 = 60 x 10-3
Rt = 500
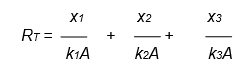
\(\begin{array}{|rcll|} \hline R_T &=& \dfrac{x_1}{k_1A} + \dfrac{x_2}{k_2A} + \dfrac{x_3}{k_3A} \\\\ &=& \dfrac{1}{A}\left(\dfrac{x_1}{k_1 } + \dfrac{x_2}{k_2 } + \dfrac{x_3}{k_3 }\right)\\ \\ \mathbf{A} & \mathbf{=} & \mathbf{\dfrac{1}{R_T}\left(\dfrac{x_1}{k_1} + \dfrac{x_2}{k_2} + \dfrac{x_3}{k_3}\right)} \\\\ &=& \dfrac{1}{500}\cdot\left(\dfrac{40 \cdot 10^{-3}}{0.2} + \dfrac{125 \cdot 10^{-3}}{0.2} + \dfrac{60 \cdot 10^{-3}}{0.5}\right) \\\\ &=& \dfrac{10^{-3}}{500}\cdot\left(\dfrac{40}{0.2} + \dfrac{125}{0.2} + \dfrac{60}{0.5}\right) \\\\ &=& \dfrac{10^{-3}}{500}\cdot\left(\dfrac{40\cdot 10}{ 2} + \dfrac{125\cdot 10}{2} + \dfrac{60\cdot 10}{5}\right) \\\\ &=& \dfrac{10^{-3}\cdot 10}{500}\cdot\left(\dfrac{40}{ 2} + \dfrac{125}{2} + \dfrac{60}{5}\right) \\\\ &=& \dfrac{10^{-3}\cdot 10}{5\cdot 10^2}\cdot\left(\dfrac{40}{ 2} + \dfrac{125}{2} + \dfrac{60}{5}\right) \\\\ &=& \dfrac{10^{-3}}{50} \cdot (20 + 62.5 + 12 ) \\\\ &=& \dfrac{94.5\cdot 10^{-3}}{50} \\\\ \mathbf{A} & \mathbf{=} & \mathbf{1.89\cdot 10^{-3}} \\ \hline \end{array}\)
I appreciate all the effort you put into helping me. 
