All Answers 357331 Answers

Thankyou

I see what he measn I'll just edited my answer the first two towards the end is meaning that he wants 1/2 to the second power you could say or squared and the two at the end is just saying to show that the two next to the 1/2 is a numerical expression so mathmatically that two is just for an example in his case he forgot to add an equals sign   

But here's my work along with it  

In previous problems I have explainded before I have stated the operations of pemdas 

1.Exponets 

2. Parenthasess 

3. Mutiplication 

4. Division 

5.  Addition

6. Subtraction 

7 + (10 − 4)2 ÷ 4 × 1/2    2  so we first take care of the parenthasses. 

7 + 6(2) ÷ 4 × 1/2    2   The next sep is multiplication 

7 + 12 ÷  1                   Now when you multipply the fraction and every thing said and done you get 4/4's and I am going to treat this as 1 

Then we divide which = 19 and when we divide by 1 we still get 19  

Now if I were to kept the four It would have been 4.75

Your question does not make sense Nickolas.

Perhaps you can fix it?

Thanks Alan.  :)

The question stipulates non-negative numbers, so only one of Rom's sets is valid.  If the question required integer solutions then (0,0,0, 2) is also a solution.  However, it specifies real numbers (not necessarily integers), so there may well be other solutions, but so far I haven't put any thought into what those might be!

The only other one I can think of is (0, 0, √2, √2).

I learned that trick from Heureka......it's probably somewhat "gimmicky," but....any port in a storm....LOL!!!

There are sheep and goats in a sheep herd. It is known that the sheep constitute 45% of the herd, and their total weight constitutes 55% of the total weight of the herd. The average weight of a goat is 81 kg. What is the average weight of a sheep?

Let's suppose that we have 100 animals and that 45 are sheep and 55 are goats

Then....the total weight of all the goats =  55 *81  = 4455kg

And the sheep  constitute  55/45 of this weight =  (55/45)  (4455)  = (11/9) (4455) = 5445 kg

So...the avg weight of a sheep  =   5445 / 45  =  121 kg

As follows:

I do not doubt you Rom but how do you know that those are the only 2 quadruples?

Hi Chris,

I really like your idea of putting it in a semicircle!      

Since  BD is a median....then AD = DC........and we can construct a circle with radius DC  = 2

And since angle B is right  and A and C lie on the diameter endpoints .....then right triangle ABC can be inscribed in the circle

Then BD is a radius   = 2.....and...in right triangle BDE,  DE = (1/2) BD = 1  ....and BE = √3

And in  right triangle BDE, angle DBE = 30°   and angle EDB = 60°

Then angle ADB is supplemental to EDB = 120°

And AD = DB.....so  in triangle ABD, angles BAD and ABD =  30°

Then, in right triangle ABC,  angle ACB = 60°

So....in  right triangle ABC....BC = (1/2) AC = (1/2)(4) = 2  and AB =  2√3

And in right triangle BCE....angle EBC = 30°....so....EC = 1/2 BC = (1/2)(2) = 1

So

AB / EC  =      [2√3] / [1]   =     =    2√3

Derpy thinks that you mean     $\sqrt7$

And LagTho thinks that you mean   $(\sqrt7)^2$

You could mean other things as well.   

You have not worded your question properly.  

First one...

The low point on the graph on  this  interval  = -36  =  relative min

The high point on the graph on this interval  = 64 =  relative max

Second one

(f + g) (x)  =   f(x) + g(x)   =  [ x^2 - 36 ]  +  [ x^3 + 2x^2 - 10  ]   =   x^3 + 3x^2 - 46

Last one

(f * g)  (x)   =  f(x) * g(x)   =  (x^4 - 9) ( x^3 + 9)  =   x^4 *x^3 + 9x^4 - 9x^3  - 9 * 9  =  x^7 + 9x^4 - 9x^3 -  81

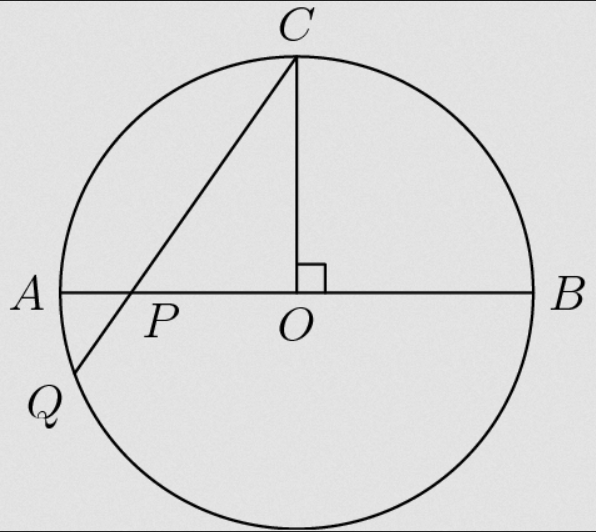
Let A, B, C be points on circle O such that AB is a diameter, and CO is perpendicular to AB.
Let P be a point on OA, and let line CP intersect the circle again at Q.
If OP = 20 and PQ = 7, find r^2, where r is the radius of the circle.

Avg rate of change =

[ f(1) - f(-1) ]                27  -  3                24  

_________      =       _______    =      _____  =    12

    1 - (-1)                        2                      2

$\text{The only two are }\\ (1,1,1,1),~(-1,-1,-1,-1)$

$A = a_{i,j},~B=b_{i,j}\\ AB-BA = \begin{pmatrix} a_{1,2} b_{2,1}-a_{2,1} b_{1,2} \\ \left(a_{1,1}-a_{2,2}\right) b_{1,2}+a_{1,2} \left(b_{2,2}-b_{1,1}\right) \\ \left(a_{2,2}-a_{1,1}\right) b_{2,1}+a_{2,1} \left(b_{1,1}-b_{2,2}\right) \\ a_{2,1} b_{1,2}-a_{1,2} b_{2,1} \\ \end{pmatrix} = 0$

$\text{From the first row we see }a_{1,2}=a_{2,1}=0\\ \text{Then from row 2, }a_{1,1}=a_{2,2}\\ \text{This agrees with row 3, and row 4 agrees with row 1 }\\ A = \lambda I_{2,2},~\lambda \in \mathbb{C}$

$\exists w_1 \ni A w_1 = \begin{pmatrix}1\\0\end{pmatrix}\\ \exists w_2 \ni A w_2 = \begin{pmatrix}0\\1\end{pmatrix}\\ B = \begin{pmatrix}w_1 &w_2\end{pmatrix}$

Degrees = 60

Radians = 1.0472

Put these approximate coordinates on a graph paper, and it's easy to say that this point lies on the unit circle. It doesn't give us any degrees, so that makes me think special right triangles. Let's call the point we have P. Draw a perpendicular line to the x axis from P, connect it to the origin, (0, 0) and connect that line to P. Given the coordinates, we can see that one leg is 1/2, and the other is $\sqrt3/2$ . Time to use Pythagoras, and square both of these numbers. 1²/2² + $\sqrt3^2/2^2$ = c². This turns out to 1/4 + 3/4 = c² . So c = 1. Since this side is twice one of the legs,this means that this triangle is a 30-60-90 triangle, so the angle is 60 degrees. To get the radians, I just looked up degrees to radians and that's what it gave me.

In case you wanted to check for yourself, formula for unit circle is x ² + y² = 1. I couldn't find out how to upload the pic. 

Hope this helps!

https://snag.gy/OKL13Y.jpg

Uuuuhhhh....where is the drawing?

Thank you so much I did not understand this problem at all before! 

Nope